理”明则“法”成——以《小数乘整数》教学为例

执教/叶菲菲　　评析/罗鸣亮

一、唤醒经验，提出问题

师：同学们，0.8×3等于？

生：2.4。

师：奇怪了，没教过你们怎么都知道，你们是怎么想的？

生：三八二十四，就是2.4。

师：2.4，为什么把小数点点在这里呢？这有道理吗？

【评析：0.8×3计算结果是许多学生已知的，但是对其计算的算理是懵懂的。课伊始，教师立足学情，快速提出问题，让学生的思考直逼知识本质。】

二、联系旧知，初感算理

师：0.8×3=2.4，你能用自己的方法来讲讲道理吗？

生：0.8×3是表示3个0.8相加，0.8+0.8+0.8=2.4。

师：对，根据乘法的意义，把新知转化为旧知，这是一种很好的解题策略。还有别的方法吗？

生：0.8 元＝8 角；8×3＝24（角）；24角＝2.4元。

师：很好，利用人民币单位间的进率把0.8元看作8角，把新知转化成旧知来解答，用整数乘法算出结果。除了购物的经验帮助我们讲清这个道理外，生活中还有吗？

生：0.8米 =8分米，8×3＝24（分米）；24分米＝2.4米（教师相应板书）。

师：是的，1米=10分米，借助长度单位的进率也能把道理说清楚。

【评析：让学生根据已有的知识经验和生活经验，从不同角度来尝试说明0.8×3=2.4的道理，感悟小数乘整数可以先转化成整数进行计算，初步沟通小数乘整数和整数乘法的联系。让学生围绕核心问题充分表达自己的想法，理清思路的同时也正是深入体悟算理算法的过程。】

三、数形结合，理解算理

师：同学们，除了运用生活经验来帮助我们讲道理，还有其他方法吗？

师：（出示小数加减法直观图的课件）谁来说说，之前咱们是用什么来帮助我们学习小数加减法的？

生：……

师：那0.8×3是不是也能用直观图来讲清道理呢？

生：能。

师：0.8×3怎么用画图来讲道理呢？同桌互相说一说。

（同桌交流，反馈）

生：把一个图形平均分成10份，0.8就有这样的8份，0.8×3就有这样的3个，就有24份。

生：0.8有8个0.1，有这样的3份，就有24个0.1，24个0.1就是2.4。

……

师：听明白了吗？你们也都是这么想的吗？让我们一起看看（播放课件），是这样的吗？好的，同学们，这个道理咱们也可以用竖式把它表示出来。

师：0.8表示 8个 0.1，8个0.1乘3就是24个0.1，24个0.1就是2.4（边讲述边板书）。

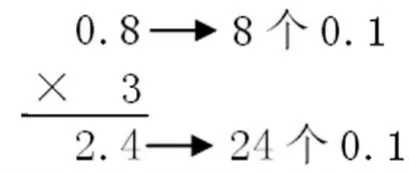
师：现在你明白2.4的这个小数点为什么要点在这儿的道理了吗？

生：因为它是24个0.1。

师：大家都看明白了其中的道理，那么，咱们还能不能举出像这样小数乘整数的例子？在自己的练习本上写一写，与同桌说一说。

【评析：脱离具体情境，让学生用小数的意义来理解算理，对学生来说是具有一定难度。本环节，教师利用学生已有的数学学习经验，让学生借助图形，于图形中理解数的意义，并借助数的意义说明算理。同时，通过让学生自主举例说理，促进了学生进一步理解算理。教师借助学生的已有学习经验，把学生不易想到但又有益于学生发展的直观模型推荐给学生，让学生借直观图来说理，使算理的阐述更为清晰、准确，培养了学生数学理解能力。】

四、沟通算理，明晰算法

师：说得真好，叶老师也来举个例子，2.16×4，这个算式与之前的算式有什么不同？

生：这个算式的小数是两位小数，前面的都是一位小数。

师：观察得很到位，那你们会算吗？试着在练习本上用竖式算一算。

（学生独立完成，请一名学生板演）

师：来和大家说说你是怎么算的？

生：我是先算6乘4等于24，写 4进 2，然后算 1乘 4等于4，4加2等于6，再算2乘 4等于8，最后再点上小数点。

师：同学们，听起来怎么这么熟悉？

生：和整数乘法一样。

师：是的，大家都是把2.16当成216来算，先算216×4，那结果怎么是8.64呢？

生：因为这是216个0.01，结果就是864个0.01，也就是8.64。（教师配合板书）

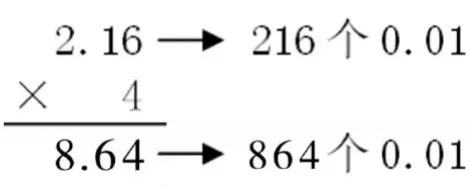
师：我们已经完成了两道题，现在让我们一起回头看，对比这两道算式在计算过程中有什么相同的地方？

生：都是先把小数看成整数来算。

师：是的，举个例子，第一道算式是把它看成8乘3，第二道算式是把它看成216乘4，都是将小数乘整数转化成整数乘整数。

师：为什么0.8×3的积是一位小数，而2.16×4的积却是两位小数？

生：因为0.8是一位小数，2.16是两位小数。

生：因为2.4是表示24个0.1，而8.64是表示864个0.01。

师：太棒了，那根据这样的想法，你能给下面算式的积点上小数点吗？

2.8×43=1204

0.103×18=1854

（学生独立完成，随后反馈）

生：2.8×43的积是120.4，2.8表示28个0.1，积就是1204个0.1。

生：2.8是一位小数，积是一位小数。

生：0.103×18的积是 1.854，0.103是三位小数，积就是三位小数，是1.854。

师：通过刚才的计算和比较，你认为咱们今天所学的小数乘整数应该怎样算？同桌互相说一说。

生：小数乘整数是先把小数看作整数来算，再点上小数点。

生：小数乘整数跟整数乘法一样，看乘数中有几位小数，积也是几位小数。

【评析：不管是小数乘法还是整数乘法的笔算，追溯其本源，都是求有几个这样的计数单位。本环节，从笔算一位小数乘法迁移到笔算两位小数乘法，让学生在自主迁移中明晰：小数乘法的笔算和整数乘法的笔算其算法是相通的，小数乘法需要再点上小数点是由其计数单位决定的。】

五、练习拓展，运用提升

1.基础练习。

师：看来大家都掌握新本领了，那咱们来一场计算比赛，比一比谁算得又对又快！第一题：8.4×6=（ ）。

师：你是怎么算的？

生：算 84×6=504，然后点上小数点，是50.4。

师：这两题，你能很快算出答案吗？说说你是怎么想的？

出示：84×0.6=（）84×0.06=（）

2.变式练习。

出示：（）×（ ）=5.04

师：猜猜这道题可能是什么？猜对了卡片送给你。

生：0.84×6，0.84 是两位小数，积就是5.04。

师：太棒了，说得很有道理，很遗憾，没猜对！还有吗？

生：8.4×0.6=5.04。

生：5.04×1=5.04。

师：他说得对吗？（揭示答案：5.04×1=5.04）

师：他说对了，那你们为什么没想到？

师：看来有时候，我们要换个思路想问题。你现在还能想到其他的算式吗？是的，实际上还有很多，我们会在后面的学习中继续学习。

【评析：计算技能的掌握需要一定的训练，但是训练中应该讲道理，让学生在理解的基础上，根据数的变化规律及算理，灵活地进行计算。教师从一位小数乘法笔算入手，通过变化因数，让学生经历从需要笔算到不笔算就能推理出积的过程，提升学生的运算能力。并在变式训练中，改变学生惯性思考方式，提升数学思维的灵活性和创新性，让精彩与众不同。】