非线性扰动方程研究平面混合层发声机制

张程远，方一红

(天津大学机械工程学院力学系，天津300072)

非线性扰动方程研究平面混合层发声机制

张程远，方一红*

(天津大学机械工程学院力学系，天津300072)

在流动过程中由脉动引起的噪声问题在自然界和工业界中广泛存在，研究流动过程中不稳定波的发声机制对于理解、预测并最终控制气动噪声有着重要意义。本文以二维Blasius相似性解作为基本流场，以超声速混合层作为研究对象，采用非线性扰动方程(NLDE)研究超声速混合层不稳定波的近场动力学特性与远场声辐射之间的内在联系。针对不同类型的对流马赫数，分别研究对流马赫数Mc=0.5(＜1)和Mc=1.2(≥1)两种情况下的扰动发声机制，结果表明:当对流马赫数Mc＜1时，流场中的发声机制主要由大尺度结构的涡条发声，且基本波与亚谐波之间的非线性作用能增强辐射强度;当对流马赫数Mc≥1时，根据扰动相速度是相对于上层还是下层自由流速度为超声速，可以进一步分为快慢两种模态，分别对快慢两种模态以及其相互作用模态进行了数值模拟研究，计算得到流场中的发声机制是以马赫波形式辐射向远场，即马赫波辐射，其辐角的计算结果与理论值相符。

非线性扰动方程;超声速混合层;对流马赫数;涡条发声;快慢模态;马赫波辐射

0 引言

流动中由脉动导致的噪声问题在航空和自然工业中广泛存在，例如发动机射流噪声、机翼和旋翼噪声、燃气噪声等，伴随着航空航天飞行器的发展，由非定常气动力产生的气动噪声对环境造成了严重地污染，气动噪声问题开始得到大家的重视，在此期间，相关的科研人员开始着手气动噪声问题的研究，随之形成了气动声学这门学科［1］。流动中的强剪切区域一般具有复杂的动力学特性，最终将导致大范围内的时间和空间尺度的湍流结构。湍流噪声是流动中的雷诺应力辐射的噪声，从稳定性理论的角度来看，对于可压缩流动来说，流体中的不稳定波与声音的产生存在着直接的联系，因此研究流动过程中不稳定波的动力学特性对于理解、预测并最终控制气动噪声是十分必要的。这也引起了学术界和工业界的日益重视［2］。

流动中不稳定波与声辐射之间是如何联系在一起的?近年来已经有许多学者开始研究二者之间的内在联系。Colonius等［3］和Bogey等［4］采用直接数值模拟研究二维平面混合层声辐射问题，Mitchell等［5］利用数值模拟的方法研究对称涡结构产生的声场，李晓东和高军辉［6］使用线性Euler方程研究二维平行剪切层声波产生和辐射，邢超和罗纪生［7］使用直接数值模拟研究声波与剪切层的相互作用，Tam等［8-9］等使用渐进展开的方法在无粘和局部平行流假设的前提下研究剪切层中不稳定波与声辐射之间的关系，Wu［10-11］使用渐进分析的方法结合三层结构理论，将流场分为粘性亚层、主层和势流层，研究了剪切层中的声辐射问题，Bertolotti等［12］使用线性抛物化稳定性方程(Parabolized Stability Equations，PSE)研究射流声辐射问题，这些研究主要还是从单个扰动波的演化性质着手，入口加入的扰动初始幅值较小，对不稳定波的非线性作用考虑较少。

相比于线性不稳定波的特性，对于非线性不稳定波的近场动力学特性和远声场辐射之间的内在联系方面的研究较少，Cheung等［13］使用线性和非线性PSE研究二维可压缩剪切层声辐射问题，在亚声速剪切层中出现了涡条结构，但是并没有很好地捕捉到远声场的特性，可能的原因是PSE在法向上采用的是齐次边界条件，而且PSE方法假设沿流向是缓慢变化，但混合层的增长速度较快，扰动在向下游演化过程中会受到强非平行性影响，这些都会影响到流场和声场信息的捕捉。

为了进一步研究剪切层中不稳定波与声辐射之间的内在关联，本文采用非线性扰动方程(Nonlinear Disturbance Equations，NLDE)研究二维超声速可压缩混合层的声辐射问题。同时考虑了非线性相互作用和非平行性的影响，数值模拟了对流马赫数Mc＜1和Mc≥1两种情况下不稳定波的扰动演化，给出了不同情况下扰动演化的计算结果，并在此基础上研究扰动波的发声机制。

1 控制方程

对当前混合层的稳定性分析，采用非线性扰动方程的分析方法，推导扰动方程的基本思想是:将二维可压缩N-S方程中的守恒量分解为基本流与扰动量之和的形式并带到N-S方程中，去掉满足定常流N-S方程的基本流项，经过化简可得到扰动方程，方程形式如下:

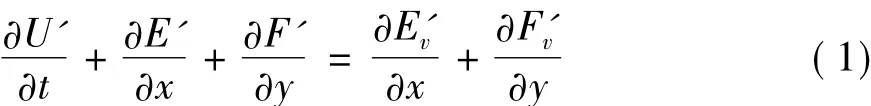
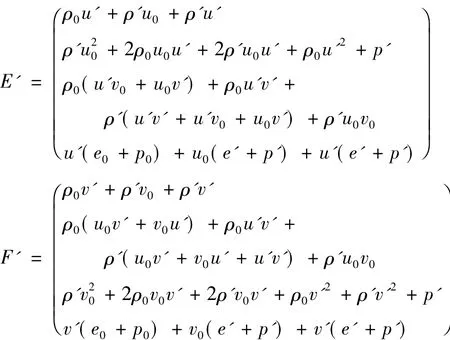
粘性扰动项:

2 差分格式和边界条件

计算过程中，粘性项采用六阶中心差分格式，具体形式如下:

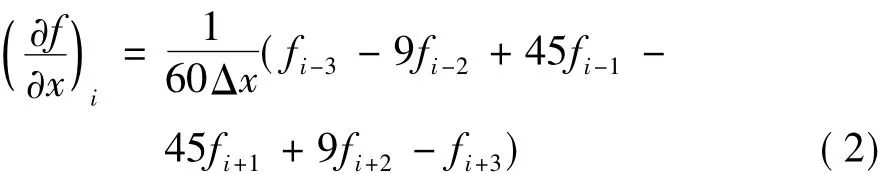
对流项采用通量分裂，对正通量E+和负通量E－在空间上采用五阶弱迎风紧致格式:

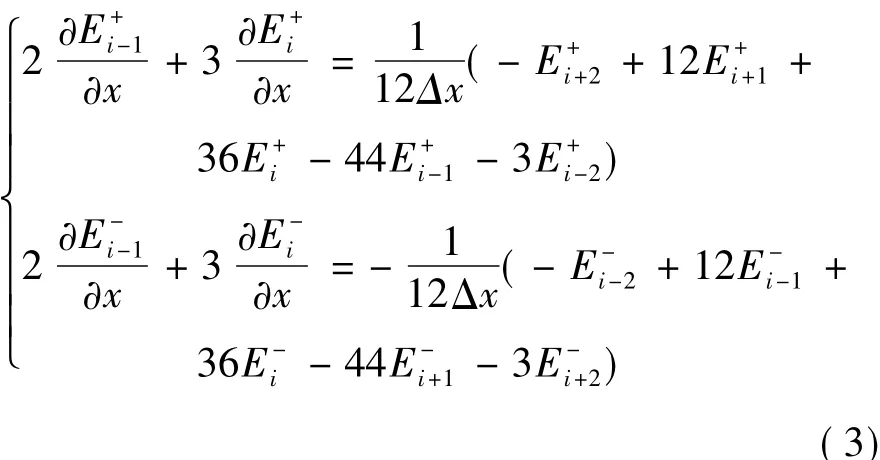
时间项采用非TVD特性的四阶四步Runge-Kutta格式:

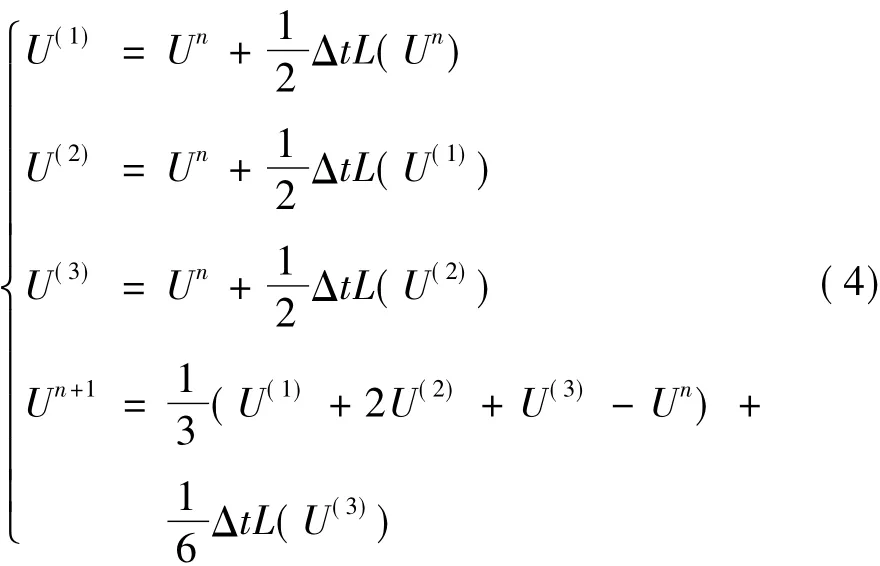
对于每一个边界，都有四个特征波穿过，其特征波的传播方向由各自的特征值正负号决定。对于超声速流，四个特征值都为正，其对应的特征波都向右传;对于亚声速流，有一个特征值为负，其它特征值为正，即三个波向右，一个波向左。本文考虑的是超声速流动。入口边界条件由线性稳定性理论给出，其扰动形式为出口边界条件由单边差分给出，同时，为了减弱出流反射波的强度，在出口处添加一段嵌边区［14］，其中预先指定的嵌边区出流处的扰动值设定为0，即Uc=0，上下边界采用完全无反射边界条件［15］。

3 数值算例

3.1 对流马赫数Mc=1.2(≥1)的情况

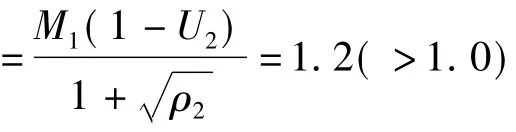
基本流通过求解定常可压缩二维边界层方程［16］得到，入口取无量纲长度δω0=1，对应的流向长度x0≈337.50，图1给出了入口处的基本流剖面。

图1 入口处基本流剖面Fig.1 Base flow profile at the inflow

由线性稳定性理论得到，对于Mc≥1.0的超声速混合层流动，同一扰动频率ω0对应两个增长波－αi，根据扰动相速度相对于自由流速度Mr，j= |ω/Re{α}－Ui|/ai(i，j=1，2)是否大于1，可以把扰动形式分为快慢两种模态［17］，当扰动相速度相对于快速流为亚声速，相对于慢速流为超声速，即Mr，1＜1.0，Mr，2＞1.0，称其为快模态;当扰动相速度相对于快速流为超声速，相对于慢速流为亚声速，即Mr，1＞1.0，Mr，2＜1.0，称其为慢模态。

下面计算在入口处分别加入不同扰动模态下的扰动演化过程，选取的扰动频率为慢模态情况下最不稳定波频率，其具体的计算参数如表1。

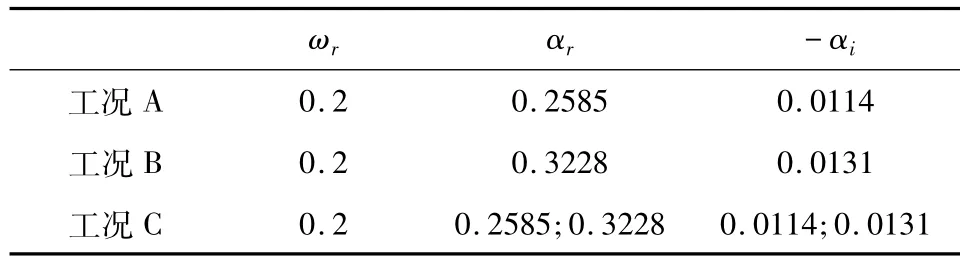
表1 入口加入不稳定波的具体参数Table 1 Parameters of inflow instability wave

图2、图3分别是工况A和工况B条件下扰动特征函数图像，分别对应于扰动快慢模态两种情况，同一扰动频率ω0=0.2，分别对应着两种不稳定扰动波，它们的增长率－αi分别为0.0114和0.0131，图2给出的是超声速扰动波快模态情形，扰动相速度相对于上层快速流为亚声速Mr，1=0.904(＜1.0)，而相对于下层慢速流为超声速Mr，2=1.496(＞1.0)，扰动的特征函数沿上层快速流方向呈指数形式衰减，而扰动沿下层慢速流方向呈正弦波的形式衰减;与图2的情况相反，图3给出的是超声速扰动波慢模态情形，扰动相速度相对于上层快速流为超声速Mr，1=1.52 (＞1.0)，而相对于下层慢速流为亚声速Mr，2=0.88 (＜1.0)，扰动的特征函数沿上层快速流方向呈正弦波的形式衰减，而扰动沿下层慢速流方向呈指数形式衰减。

为了验证程序，当前用扰动方程计算了慢模态下最不稳定频率ω=0.2的扰动波的演化，初始幅值A0=0.0001，图4给出了扰动方程与LST的计算结果，二者吻合的很好，表明扰动方程程序的正确性。

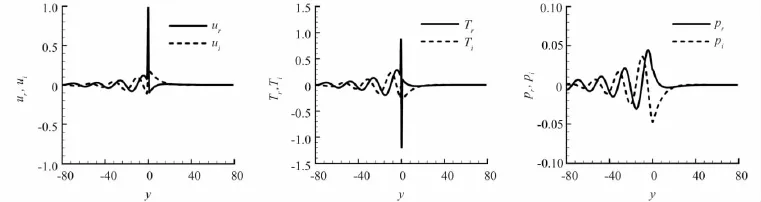
图2 快模态的特征函数图像Fig.2 Eigenfunction for fast mode

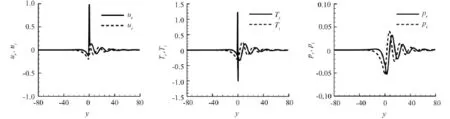
图3 慢模态的特征函数图像Fig.3 Eigenfunction for slow mode

图4扰动波幅值演化，ω=0.2，A0=0.0001Fig.4 Amp lification of the disturbance，ω=0.2，A0=0.0001

图5、图6分别给出在入口处加入A、B工况下的不稳定波，初始幅值都给A0=0.005，其扰动向下游演化过程中的压力扰动等值线p1。

比较A、B两种工况的压力等值线图，可以看出对于扰动相速度相对于自由流速度为超声速(Mr，j＞1.0)的部分，压力扰动以一定的角度向远场辐射，形成马赫波辐射，通过马赫角的计算公式μ= arcsin(1/Mr，j)可以求出快模态扰动的理论马赫角为μ≈41.9°，由图5的压力等值线求得辐角μ≈40.7°，与理论值相符。同理，由图6的慢模态等值线可以求得马赫角为μ≈40°，也与理论值μ≈41.0°相符。

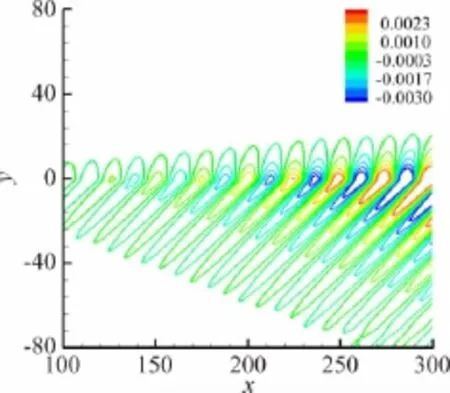
图5 加入快模态扰动压力等值线Fig.5 Pressure contours for fast mode

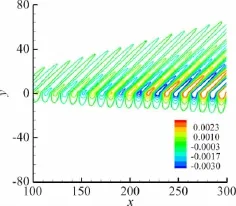
图6 加入慢模态扰动压力等值线Fig.6 Pressure contours for slow mode

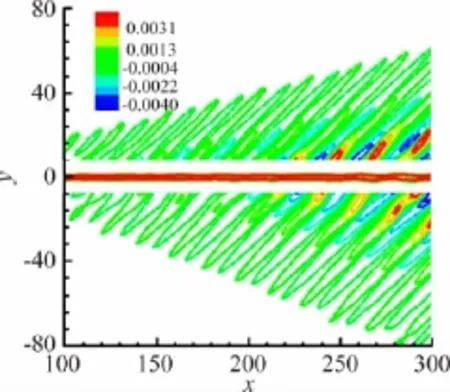
图7 加入快慢模态的扰动压力等值线Fig.7 Disturbance pressure contours for fast and slow mode

在入口处同时加入快慢模态的扰动波，得到图7所示的近场展向涡量和远场扰动压力等值线，它兼有二者的特性，扰动压力向自由流两侧方向以马赫波的形式辐射，从近场展向涡量ωz等值线看，没有出现大尺度涡结构，图8对应着基本波能量幅值E10与其倍频波的能量幅值E20。

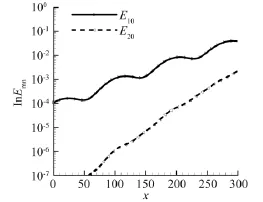
图8 基本波与其倍频波的能量幅值曲线Fig.8 Energy for the fundamental and first harmonic mode

因此，对于Mc≥1的超声速混合层流动，其发声机制主要是不稳定波以马赫波的形式向远场辐射。

3.2 对流马赫数Mc=0.5(＜1.0)的情况

利用线性稳定性理论，可以求出入口处所加的扰动的特征值和特征函数，计算求出的具体参数见表2。

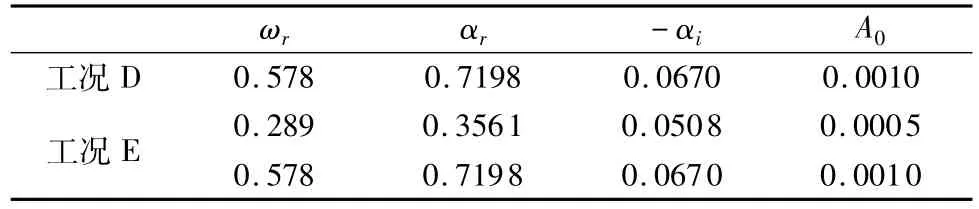
表2 入口加入不稳定波的具体参数Table 2 Parameters of inflow instability wave

图9给出了最不稳定波ω0=0.578对应的扰动特征函数幅值曲线，可以看出扰动特征函数幅值以指数形式向自由流两侧快速衰减。

图10、图11分别是在入口处加入工况D和E情况下的扰动波，使用非线性扰动方程(NLDE)计算得到扰动向下游演化过程中的远场压力等值线p和近场展向涡量云图ωz，图12是其两组工况下所对应的能量幅值曲线E。

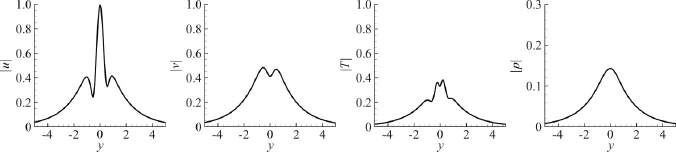
图9 特征函数幅值曲线Fig.9 Amp litudes curve of the eigenfunction

从图10的近场涡量等值线可以看到明显的大尺度涡结构，伴随着涡结构向下游演化，其扰动压力直接辐射向自由流远场，涡结构形成位置在x≈100处，从图12的能量幅值曲线上看，在此处，能量幅值达到最大，且正好对应于远场扰动压力开始辐射的位置。

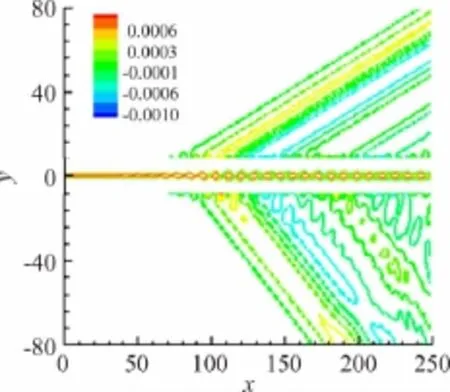
图10 工况D远场压力和近场涡量云图Fig.10 Contours of the far-field pressure and nearfield spanw ise vorticity for case D

图11是在入口处加入基本波与亚谐波的计算结果，与在入口处只加入基本波的情况相似，其近场区出现大尺度涡结构，涡结构形成的位置与远场压力辐射位置相对应，不同的是，涡结构在更下游的位置处发生了涡与涡之间的合并，其涡合并发生在x≈190处，涡合并现象是基本波与亚谐波的非线性相互作用导致，图12中的能量幅值曲线显示在涡合并处，基本波与亚谐波的能量都处于峰值，此时，它们之间的非线性作用是最强的，从远场压力等值线图可以看出它们的压力强度也同时达到最大。

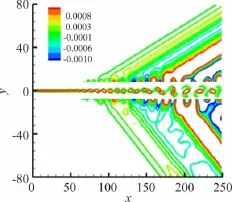
图11 工况E远场扰动压力和近场涡量云图Fig.11 Contours of the far-field pressure and near-field spanw ise vorticity for case E

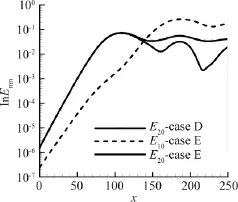
图12 基本波与其倍频波的能量幅值曲线Fig.12 Am p litudes of energy for the fundamental and subharmonic mode

因此，对于对流马赫数Mc＜1.0的超声速混合层，其发声机制主要是由大尺度涡结构及其合并引起，且基本波与亚谐波之间的非线性相互作用能增强声辐射强度。

4 结论

本文采用非线性扰动方程(NLDE)研究了超声速情况下扰动的动力学特性和远场发声机制间的关联，分析了对流马赫数Mc=0.5(＜1)和Mc=1.2 (≥1)两种情况下不稳定波的发声机制。得到了以下几点结论:

1)对流马赫数Mc≥1.0的情况，同一频率ω0的扰动对应着两个不同的不稳定波－αi，分别对应着快慢两种模态，其扰动特征函数呈现两种完全不同的形式。

2)分别对快慢两种扰动模态及其相互作用进行数值模拟研究，计算得到流场中不稳定波的发声机制:压力扰动以马赫波形式向远场辐射，即马赫波辐射。

3)对于Mc＜1.0的情况，非线性扰动方程(NLDE)能够准确捕捉到大尺度涡结构，并在下游处捕捉到涡对合并现象。

4)对于Mc＜1.0的情况，不稳波产生远声场的机理主要是大尺度涡运动及涡对的合并，而基本波与亚谐波之间的非线性相互作用能明显增强声辐射的强度。

［1］Hu Guoqing.Numerical simulation of aeroacoustic field generated by compressible flow［D］.Beijing:Institute of Mechanics，Chinese Academy of Sciences，2001.(in Chinese)胡国庆.可压缩流气动声场的数值模拟［D］.北京:中国科学院力学研究所，2001.

［2］Ju Hongbin，Shen Mengyu.Problem about computational aeroacoustics，methods and progress［J］.Mechanics in Engineering，1995，17(5):1-10.(in Chinese)居鸿宾，沈孟育.计算气动声学的问题，方法与进展［J］.力学与实践，1995，17(5):1-10.

［3］Colonius T，Lele S K，Moin P.Sound generation in a mixing layer［J］.Journal of Fluid Mechanics，1997，330:375-409.

［4］Bogey C，Bailly C，Juvé D.Numerical simulation of sound generated by vortex pairing in a mixing layer［J］.AIAA Journal，2000，38(12):2210-2218.

［5］Mitchell B E，Lele S K，Moin P.Direct computation of the sound generated by vortex pairing in an axisymmetric jet［J］.Journal of Fluid Mechanics，1999，383:113-142.

［6］Li Xiaodong，Gao Junhui.Numerical simulation of sound generation and radiation from a 2D parallel shear layer［J］.Journal of Aerospace，2003，24(1):6-9.(in Chinese)李晓东，高军辉.二维平行剪切层声波产生和辐射的数值模拟［J］.航空学报，2003，24(1):6-9.

［7］Xing Chao，Luo Jisheng.Numercial simulation of mixing layer effect on sound waves［J］.Journal of Aerospace Power，2005，20(1):8-12.(in Chinese)邢超，罗纪生.声波与剪切流作用的数值模拟［J］.航空动力学报，2005，20(1):8-12.

［8］Tam C K W，Morris P J.The radiation of sound by the instability waves of a compressible plane turbulent shear layer［J］.Journal of Fluid Mechanics，1980，98(02):349-381.

［9］Tam C K W，Burton D E.Sound generated by instability waves of supersonic flows.Part 1:two-dimensional mixing layers［J］.Journal of Fluid Mechanics，1984，138:249-271.

［10］Wu Xuesong.Generation of sound and instability waves due to unsteady suction and injection［J］.Journal of Fluid Mechanics，2002，453:289-313.

［11］Wu Xuesong.Mach wave radiation of nonlinearly evolving supersonic instability modes in shear layers［J］.Journal of Fluid Mechanics，2005，523:121-159.

［12］Bertolotti F，Colonius T.On the noise generated by convected structures in a Mach 0.9 hot，turbulent jet［J］.AIAA Paper，2003，1062:2003.

［13］Cheung L C，Lele S K.Linear and nonlinear processes in twodimensional mixing layer dynamics and sound radiation［J］.Journal of Fluid Mechanics，2009，625:321-351.

［14］Qian Lin.The numerical study of the enhancement effect in 3D supersonic mixing layer with swirl［D］.Tianjin University，2007.(in Chinese).钱琳.三维超声速旋转混合层增混作用的数值研究［D］.天津大学，2007.

［15］Ju Hongbin.Non-reflective boundary conditions and sound source modeling in computational aeroacoustics［J］.Shanghai Jiaotong University，1998，32(7):36-39.(in Chinese)居鸿宾.气动声学数值模拟中无反射边界处理及声源模型的建立［J］.上海交通大学学报，1998，32(7):36-39.

［16］Day M J，Mansour N N，Reynolds W C.Nonlinear stability and structure of compressible reacting mixing layers［J］.Journal of Fluid Mechanics，2001，446:375-408.

［17］Fu Dexun，Ma Yanwen，Li Xinliang，Direct numerical simulation of compressible turbulent flow［M］.Beijing:Science Press，2010.(in Chinese)傅德薰，马延文，李新亮.可压缩湍流直接数值模拟［M］.北京:科学出版社，2010.

Studing sound generation mechanism s of m ixing layer using nonlinear disturbance equations

Zhang Chengyuan，Fang Yihong*
(Department of Mechanics，School of Mechanical Engineering，Tianjin University，Tianjin 300072，China)

The noise problem caused by pulse exists in the aviation and natural industry，studying sound generation mechanism of the unstable wave is of important significance for understanding，predicting and controlling the aerodynamic noise.In this paper，Nonlinear Disturbance Equation(NLDE)is used to study the relationship between near field dynamic characteristic and the far field sound radiation for supersonic mixing layer.For different types of convective Mach number，disturbance pressure are selected and calculated respectively.It is gained two different sound generation mechanisms.When the convective Mach number of supersonic mixing layer is less than 1，the sound is generated by the largescale vortex structure in near-field.Otherwise，the generation of sound is depended on whether the phase velocity of disturbance is supersonic relative to the upper flow or not.It turned out that the supersonic part of the disturbance pressure radiate to far-field at a fix angle，that is so called Mach wave radiation.The calculated angle of Mach wave is consistent with the theoretical one.

nonlinear disturbance equations;supersonic mixing layer;convective Mach number; noise generation by vortex pairing;fast and slow mode;Mach wave radiation

V212.1

A

10.7638/kqdlxxb-2014.0117

0258-1825(2016)05-0659-07

2015-01-15;

2015-04-15

国家自然科学基金(11332007，10972156)

张程远(1990-)，男，福建，硕士研究生，主要从事边界层转捩预测的研究.E-mail:zhangcy9798@163.com

方一红*，副教授，主要从事流动稳动性和空气动力学.E-mail:yhfang@tju.edu.cn

张程远，方一红.非线性扰动方程研究平面混合层发声机制［J］.空气动力学学报，2016，34(5):659-665.

10.7638/kqdlxxb-2014.0117 Zhang C Y，Fang Y H.Studing sound generation mechanisms of mixing layer using nonlinear disturbance equations［J］.Acta Aerodynamica Sinica，2016，34(5):659-665.