特高压八分裂导线尾流驰振研究

严波，蔡萌琦，何小宝，周林抒

(1.重庆大学航空航天学院，重庆400044; 2.重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆400044)

特高压八分裂导线尾流驰振研究

严波1，2，*，蔡萌琦1，何小宝1，周林抒1

(1.重庆大学航空航天学院，重庆400044; 2.重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆400044)

由于多分裂导线的子导线排列密集，尾流引起的驰振问题可能会严重危害输电系统的安全运行。为研究特高压八分裂导线的尾流驰振特征，通过风洞试验测量了八分裂导线各子导线的气动力系数随风攻角的变化情况，可以看出:由于子导线之间尾流的干扰，八根子导线的气动力系数存在较明显差异，尤其是当子导线处于上风子导线的尾流区时，作用于其上的阻力会明显下降;同时，利用ABAQUS有限元软件模拟研究了档距分别为308 m和405m的两条八分裂孤立档线路的尾流驰振过程，基于该数值模拟结果，可以分析得到:八分裂导线尾流驰振存在一个临界风速，当风速小于临界风速时，没有发生尾流驰振现象;当线路发生尾流驰振时，子导线的运动轨迹近似为椭圆;在相同风速下，大档距线路的尾流驰振幅值大于小档距线路。

八分裂导线;空气动力特性;尾流驰振;数值模拟

0 引言

特高压输电线路是我国电网的大动脉，其一般采用八分裂或六分裂导线。由于多分裂导线的子导线排列密集，尾流引起的驰振问题可能更加突出。长时间的尾流驰振会引起导线和金具的疲劳破坏，严重时甚至产生碰线“鞭击”现象，严重危害输电系统的安全运行。尾流驰振的研究对其防治技术的开发具有十分重要的意义。

关于分裂导线尾流驰振的研究国际上出现较早［1-6］。Price等［1］利用风洞试验测量了一种表面光滑的导线和两种绞股导线在两种湍流度、不同Reynolds数下，下风子导线的升力系数和阻力系数与其在尾流区中的位置之间的关系。Wardlaw等［2］对分裂导线的气动特性和次档距振动问题进行了研究，他们利用风洞试验测量了二分裂、四分裂和八分裂导线的气动系数，在风洞中实施了节段模型的驰振模拟试验，并在此基础上用理论简化模型分析了分裂导线的次档距振动。Brzozowski等［3］基于线性化动力方程研究了分裂导线次档距振动的不稳定边界，指出增大分裂导线的扭转刚度可提高整档的稳定性。Rawlins等［4］采用传递矩阵方法和波传播理论分析研究了导线的次档距振动特性。Braun等［7］研究了模拟多分裂导线气弹性问题的二维数值方法，考虑了流体的可压缩、粘性、流体和固体之间的耦合作用，并利用该二维模型模拟分析了双分裂、三分裂和四分裂导线的尾流驰振动力失稳问题。在国内也开展了该项研究。叶志雄［8］分析了分裂导线次档距振动的影响因素，讨论了多分裂导线最大次档距的计算方法。陈元坤［9］建立了双分裂导线次档距振动的二自由度和四自由度振动方程，并利用非线性有限元法分析了导线倾角、间隔棒布置和风速对次档距振动的影响。近年来，严波等［10］采用数值模拟方法研究了四分裂导线的尾流驰振问题。目前，尚未见到采用三维有限元方法模拟研究特高压八分裂导线尾流驰振问题的工作。

本文首先利用风洞试验测量八分裂绞股裸导线的空气动力系数随风攻角的变化，进而建立典型线路的三维有限元模型，模拟在不同风速下线路的尾流驰振过程，进而分析八分裂导线尾流驰振的轨迹、频率和振幅等。

1 八分裂导线空气动力特性

八分裂导线的子导线排列密集，其空气动力特性复杂。为研究驰振问题，利用风洞试验测量各子导线的气动系数随风攻角的变化曲线。试验在中国空气动力研究与发展中心1.4m×1.4m低速风洞中完成，该风洞为直流式低速风洞，截面形状为切角矩形，试验段长2.8m，风速范围为0～65m/s。

以八分裂导线8XLGJ-500/35为对象，子导线的直径为30mm，相邻子导线之间的间距为400mm。采用真实导线段作为试验模型，可以考虑导线表面绞股线对气动特性的影响。导线模型段长度为800mm，八根子导线安装在上下两块平行的圆板上，圆板通过支撑杆与转盘连接。试验时可通过同步转动转盘以改变风攻角。利用安装在测力导线模型两端的测力天平测量作用于子导线上的升力、阻力和扭矩。导线模型和测力天平的安装方式如图1所示，风洞试验模型如图2所示。在－180°～180°风攻角范围内测量各子导线的气动力，每隔5°测量一个点。

各子导线的阻力系数、升力系数和扭矩系数定义如下［11］:

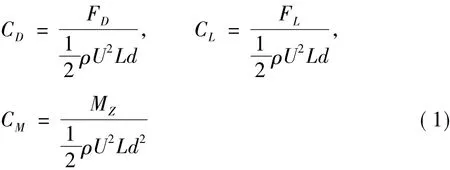
式中:FD、FL和MZ分别为作用于导线上的阻力、升力和扭矩;ρ为试验气温下的空气密度;U为来流风速;L为导线模型的有效长度;d为导线的直径。

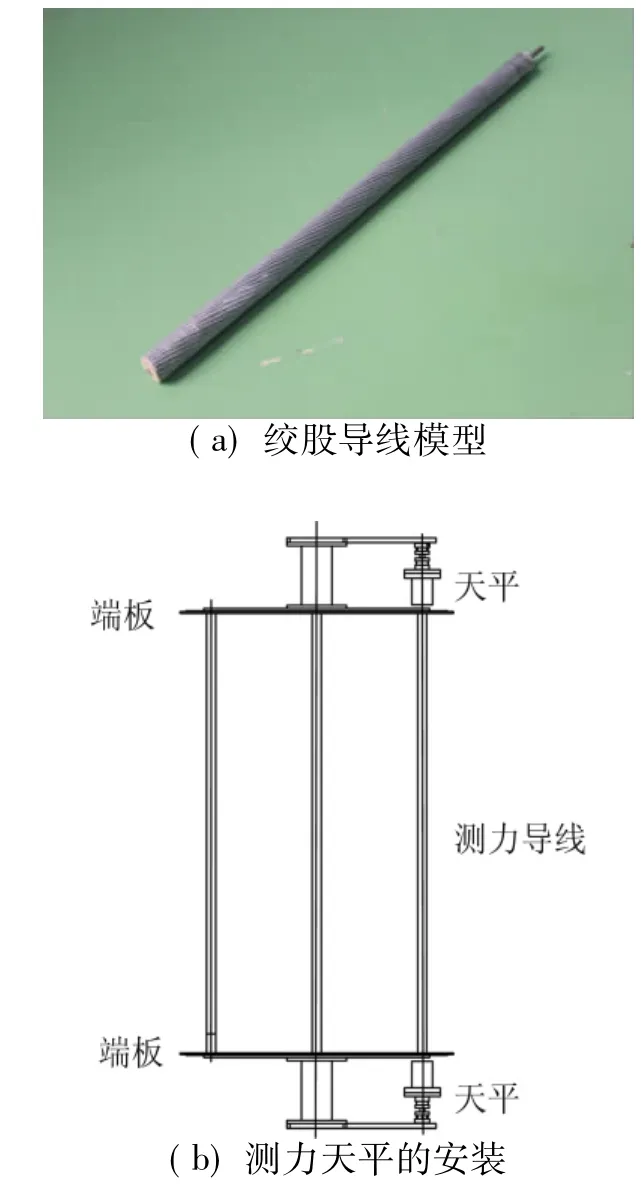
图1 导线模型和测力天平安装方式Fig.1 Test model of conductor and installation of strain balance

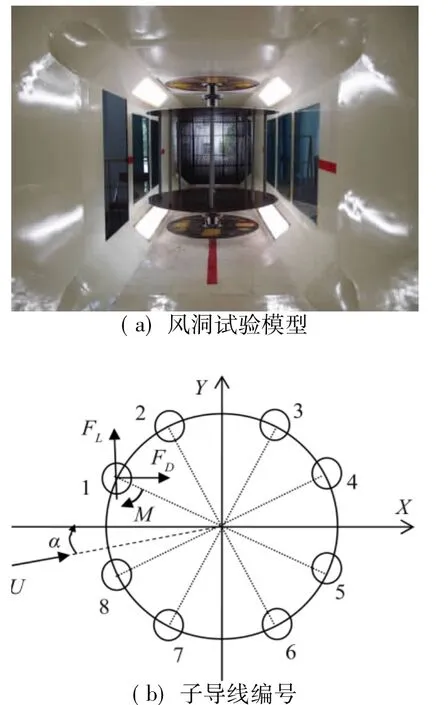
图2八分裂导线气动特性风洞试验模型Fig.2 W ind tunnel test model of eight bundle conductor

图3所示为风速10 m/s时，测得的八分裂导线各子导线的气动系数随风攻角的变化曲线。从图中可以看出，由于尾流的影响，八根子导线的空气动力系数存在较明显的差异。当子导线处于上风子导线的尾流区时，作用于其上的阻力会明显下降，同时还会受到升力的作用，而在整个风攻角范围内，扭矩作用相对较小。值得一提的是，子导线的阻力系数在特定的风攻角附近出现“跳跃”，这是由于该子导线正好处于背风侧，受迎风侧子导线的遮挡作用所致。

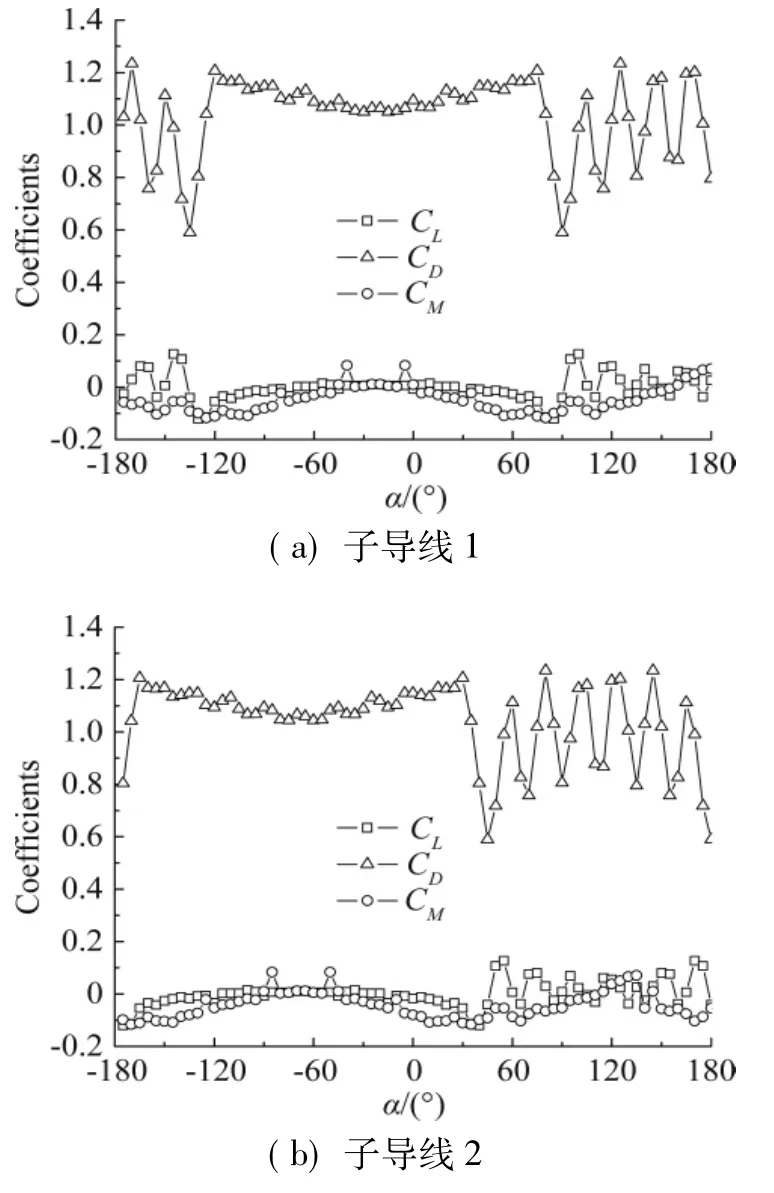
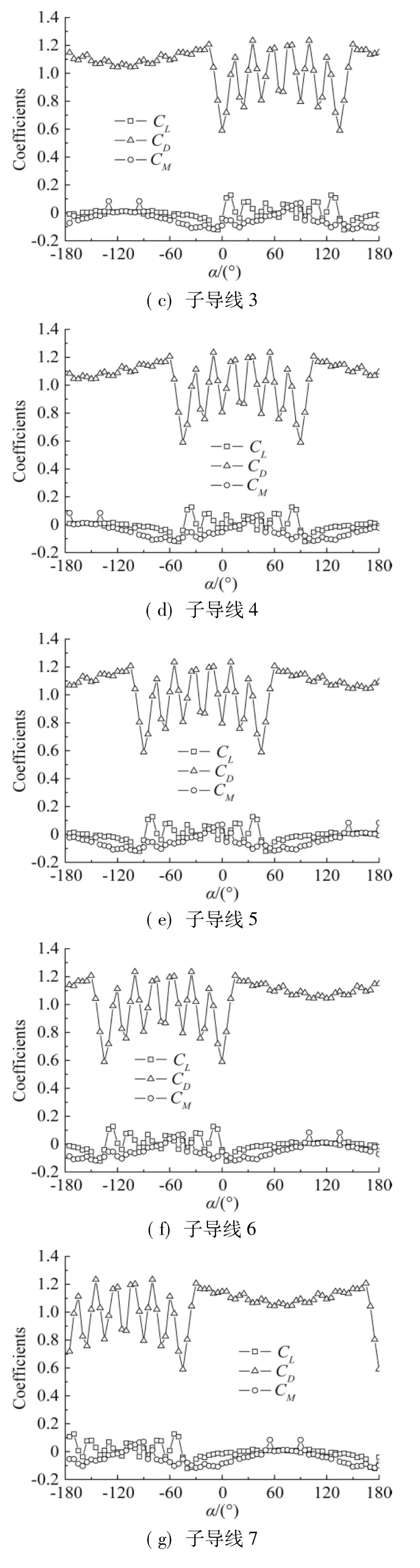
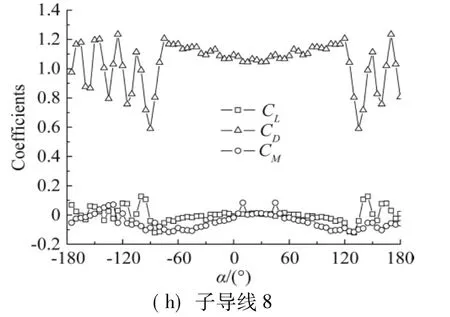
图3 八分裂导线空气动力系数随风攻角的变化(风速:10m/s)Fig.3 Aerodynam ic coefficients of eight bund le conductor (w ind speed:10m/s)

2 线路有限元模型及其动力特性

2.1 线路参数及有限元模型

以档距分别为308m和405m的两条八分裂孤立档线路为研究对象。导线型号与风洞试验中的相同，其参数如表1中所列。安装的每个子间隔棒的质量为17.5 kg。子间隔棒的布置尚无行业标准，参考现行110～500 kV输电线路设计规程［12］确定。

档距为308m的线路上安装6个子间隔棒，第1个子间隔棒距离左端31m，其余依次增加52m、46m、56m、44m和51m，导线的初始张力为28.4kN。档距为405m的线路上安装8个子间隔棒，第1个子间隔棒距离左端30m，其余依次增加50m、46m、55m、46m、56m、43m和51m，导线的初始张力为27.9kN。

会计电算化通俗来讲就是利用计算机进行会计工作，在会计工作中应用了电子计算机技术。具体的说，就是利用电子计算机完成会计工作过程，完成在人很难完美进行的会计工作。以电子计算机为主，运用当代电子技术，运用当代信息技术，这是会计电算化的核心构成，会计电算化是一个使用电子计算机为核心工具实现的会计工作的信息系统。对于自动处理数据是一大进步，会计电算化也能改变传统的手工会计信息系统。会计电算化是会计发展的必然结果。

导线的阻尼采用Rayleigh阻尼模型:

式中C、M和K分别为阻尼矩阵、质量矩阵和刚度矩阵。根据文献［13，14］，对于输电导线，系数β几乎为零。裸导线的阻尼比取1.0%。

表1 导线的几何和物理参数Table 1 Geometric and physical parameters of conductor

导线可视为柔索结构，在ABAQUS软件中，将空间杆单元的材料性质设置为不可压缩即可得到索单元，用索单元离散各子导线。此外，子间隔棒的刚度较导线大，可简化为正方形框，用空间梁单元模拟。分裂导线有限元建模方法详见文献［15］，建立的两条线路的有限元模型如图4所示。网格收敛性检查表明，模拟导线的单元长度取0.5m时可以满足精度要求。

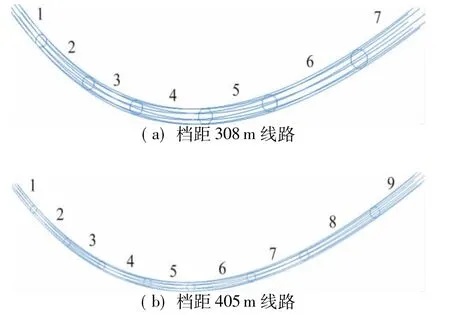
图4 典型八分裂导线线路有限元模型Fig.4 Finite element model of typical eight bundle conductor lines

2.2 线路的动力特性

为分析导线的驰振特征，首先利用ABAQUS有限元软件，计算该两条线路的动力特性，获得其低阶固有频率和模态。

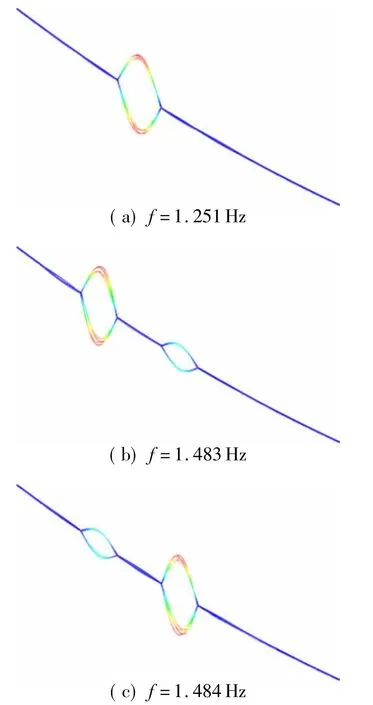
图5 档距405m线路典型次档距局部模态及其固有频率Fig.5 Local sub-span modes and natural frequencies of eight bundle conductor line w ith unequally arranged spacers

计算结果表明，档距为405m的线路在0.16～1.17Hz频率范围内为线路整体的面内、面外和扭转模态;从频率1.19 Hz开始出现较密集的次档距局部模态。如图5所示为该线路典型的次档距局部模态及其对应的固有频率。类似的分析得到档距308 m线路的低阶固有频率和模态，在0.21～1.10 Hz频率范围内为线路整体的面内、面外和扭转模态;从频率1.18Hz开始出现较密集的次档距局部模态。

3 尾流驰振模拟及其特征

从试验得到的气动系数曲线可知，作用于裸导线上的扭矩很小，可以忽略不计。作用在导线上的气动荷载随风攻角变化，与导线的运动状态有关。根据式(1)，作用在单位长度导线上的气动力由下式确定:

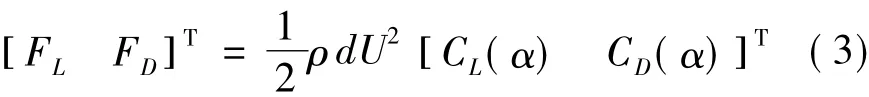
其中α为风攻角。导线运动过程中风攻角α可以由下式确定:

式中，θ为初始风攻角，V为导线垂直方向的速度。

作用于导线上的气动载荷利用ABAQUS用户自定义单元子程序UEL实现。在UEL中定义一个无质量无刚度的单元，该单元与模拟导线的索单元共结点。在调用该用户单元时可以获得每一时刻结点的位移和速度，利用图3所示的气动系数曲线，由式(4)和式(3)确定作用在各个结点上的气动载荷。由于气动载荷单元与离散导线的索单元共结点，通过这种方式即可将气动载荷施加到索单元上。这一方法类似于舞动模拟中的气动载荷的施加方法，详见文献［12］。数值模拟中考虑了线路的几何非线性。

3.2 尾流驰振特征分析

利用前述方法对线路在稳定风作用下的驰振过程进行数值模拟。模拟计算了10 m/s、12 m/s、14 m/s、16m/s和20m/s五种风速下该两条八分裂导线线路的尾流驰振过程。假设来流初始风攻角均为0°。

现在分析档距405m线路在风速16m/s下的尾流驰振。图6所示为该线路在典型时刻的运动形态。可见，线路发生了明显的次档距振动，显然这些次档距振动为尾流驰振。

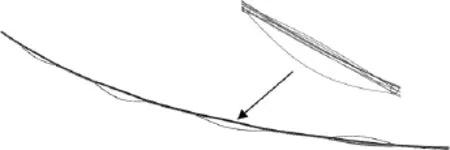
图6档距405m线路典型时刻的振动形态(风速:16m/s;位移放大10倍)Fig.6 Vibration shape of 405m-span line at typical time (w ind speed:16m/s;displacement am plification factor:10)

图7 所示为该线路各次档距中点各子导线的运动轨迹，各次档距的编号参见图4。可见，在尾流干扰作用下，次档距2、4、6、8中处于下风尾流区的子导线发生了明显的尾流驰振现象，驰振运动的轨迹近似为椭圆状。各次档距中子导线6的驰振幅值较其它子导线大，最大振动幅值出现在次档距4的中点，其次是次档距6的中点。由于八分裂导线子导线密集，绕流场非常复杂，子导线6位于导线束的后下方，受尾流影响较明显，可能是导致其振动幅值较大的原因。但这一问题尚值得深入研究。

除了次档距振动外，线路还发生了整体的风偏。从图7中可以看出，次档距1和9靠近线路两端，整体水平偏摆较小;次档距5处于档中间，导线整体向右的偏摆最大。此外，线路几乎没有发生整体的垂直和水平振动，这可从后面的位移频谱分析结果看到。

为分析该线路的驰振特征，对次档距4中点处各子导线的位移进行频谱分析。各子导线的频谱曲线出现峰值对应的频率相同，限于篇幅，图8仅给出子导线6的结果。可见，垂直位移和水平位移均在频率1.224Hz处出现峰值。由2.2节线路动力特性分析结果可知，该峰值对应的频率在次档距局部振动模态范围内，表明导线的运动没有出现整体振动，仅出现了次档距振动。值得一提的是，尽管线路没有整体振动，但在水平风荷载作用下却出现了稳定的风偏。

图9所示为档距308 m线路在风速16 m/s下各次档距中点子导线的运动轨迹，可明显观察到尾流驰振现象，导线的驰振运动轨迹也近似为椭圆。各次档距中仍然是子导线6的驰振幅值大于其它子导线，最大振动幅值出现在中间次档距，即次档距4的中点。

由图7和图9的结果可见，该两条线路的最大次档距振动发生在线路靠近档中间的次档距中，由于间隔棒的非均匀布置，最大次档距振动不一定发生在整档线路的中点。

表2所列为两条线路在不同风速下子导线的最大次档距振动幅值。从表中结果可见，在风速10m/s时两条线路均没有发生振动，即没有发生尾流驰振现象，因而尾流驰振存在一个临界风速。随着风速的增大，两条线路的次档距振动幅值均增大。在相同风速下档距为405m线路的驰振幅值比档距308m线路的略大。

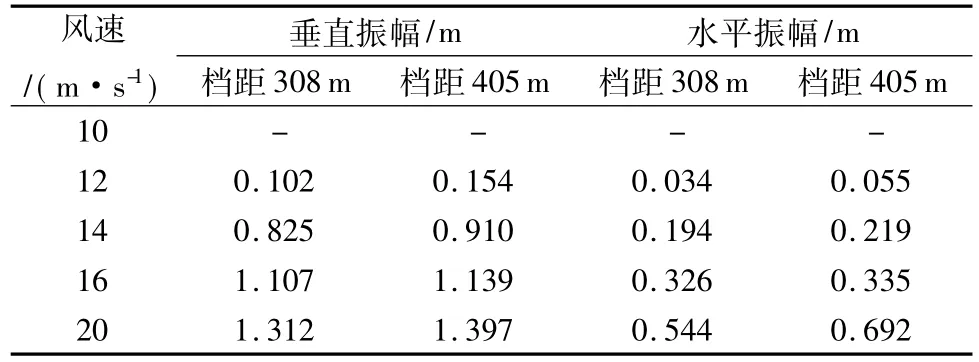
表2 不同风速下线路子导线的最大次档距振动幅值Table 2 M aximum vibration amplitudes of sub-conductors at various w ind speeds

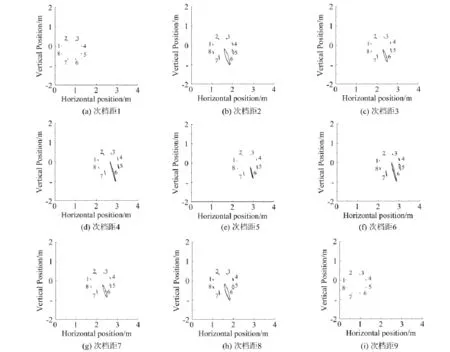
图7 档距405m线路各次档距中点子导线运动轨迹(风速:16m/s)Fig.7 Galloping traces at sub-span m id-points of 405m-span line(w ind speed:16m/s)

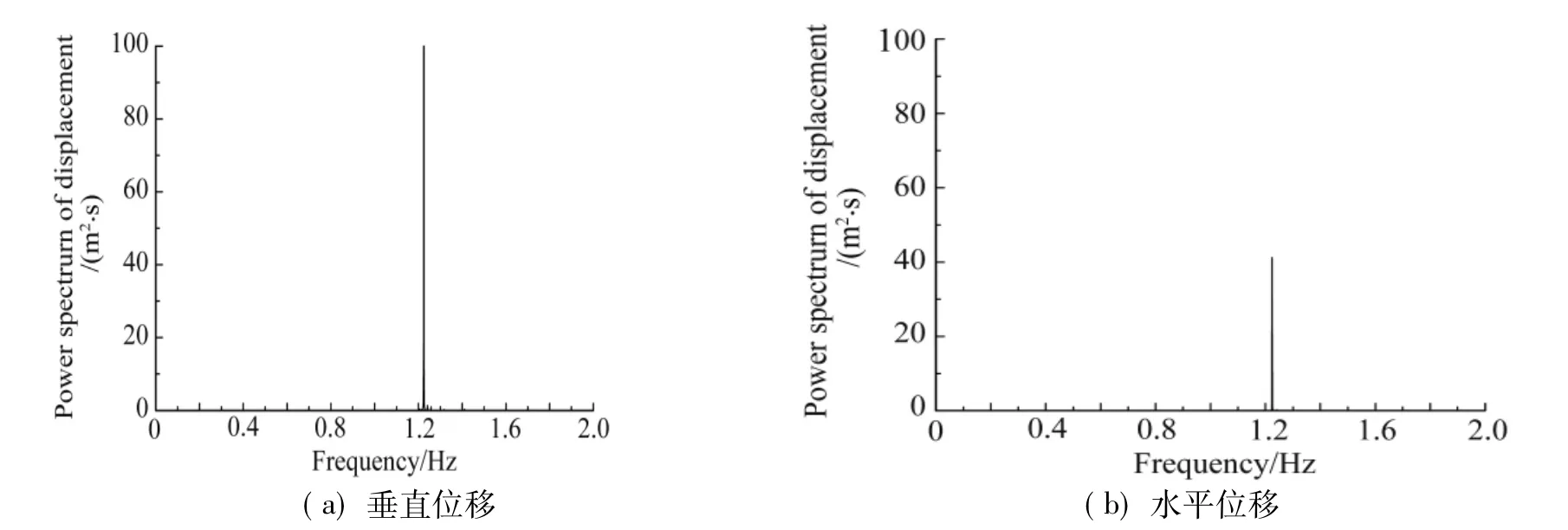
图8 档距405m线路次档距4中点子导线6的位移频谱Fig.8 Displacement spectra of sub-conductor 6 at m id-point of sub-span 4 of 405m-span line

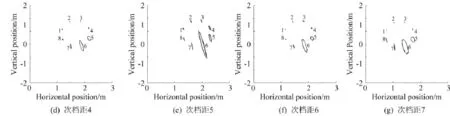
图9 档距308m线路各次档距中点子导线运动轨迹(风速:16m/s)Fig.9 Galloping traces at sub-span m id-points of 308m-span line(w ind speed:16m/s)

4 结论

本文利用风洞试验测量了八分裂绞股裸导线的气动系数，进而用有限元方法模拟了不同档距线路在不同风速下的尾流驰振过程，得到如下结论:

1)八分裂导线各子导线的气动系数随风攻角的变化规律较复杂，上风子导线尾流对下风子导线的气动特性影响明显，处于尾流区中的子导线的阻力明显下降，同时会受到升力的作用，但扭矩很小;

2)线路发生尾流驰振时，子导线的运动轨迹近似为椭圆，与实际观察到的少分裂导线的驰振现象一致;

3)最大次档距振动发生在线路靠近档中间的次档距中，由于间隔棒的非均匀布置，最大次档距振动不一定出现在整档线路的中点;

4)尾流驰振存在一个临界风速，当风速大于临界风速时，分裂导线尾流驰振振幅随风速的增大而增大，在相同风速下，大档距线路的尾流驰振幅值大于小档距线路。

［1］Price S J.Wake induced flutter of power transmission conductors［J］.Journal of Sound and Vibration，1975，38:125-147.

［2］Wardlaw R L，Cooper K R，Ko R G，et al.Wind tunnel and analytical investigation into the aeroelastic behavior of bundled conductors［J］.IEEE Transactions on Power Apparatus and Systems，1975，94(2):642-651.

［3］Brzozowski V J，Hawks R J.Wake-induced full-span instability of bundle conductor transmission lines［J］.AIAA Journal，1976，14 (2):179-184.

［4］Rawlins C B.Fundamental concepts in the analysis of wake induced oscillation of bundled conductors［J］.IEEE Transactions on Power Apparatus and Systems，1976，95(4):1377-1393.

［5］Rawlins C B.Extended analysis of wake-induced oscillation of bundled conductors［J］.IEEE Transactions on Power Apparatus and Systems，1977，96(5):1681-1689.

［6］Hardy C，Van Dyke P.Field observations on wind-induced conductor motions［J］.Journal of Fluids and Structures，1995，9: 43-60.

［7］Braun A L，Awruch A M.Aerodynamic and aeroelastic analysis of bundled cables by numerical simulation［J］.Journal of Sound and Vibration，2005，284:51-73.

［8］Ye Zhixiong.Aeolian vibration and subspan oscillation analysis on transmission line［D］.Wuhan:Huazhong University of Science and Technology，2009.(in Chinese)叶志雄.输电线微风振动及次档距振荡控制研究［D］.武汉:华中科技大学，2009.

［9］Chen Yuankun.Aeolian vibration and subspan oscillation analysis on bundle conductors［D］.Huazhong University of Science and Technology，2011.(in Chinese)陈元坤.分裂导线的微风振动与次档距振荡研究［D］.华中科技大学，2011.

［10］Yan Bo，Cai Mengqi，Lyu Xin，et al.Numerical simulation on wake galloping of quad bundle conductor［J］.Journal of Vibration and Shock，2015，34(1):182-189.(in Chinese)严波，蔡萌琦，吕欣，等.四分裂导线尾流驰振数值模拟研究［J］.振动与冲击，2015，34(1):182-189.

［11］Hu J，Yan B，Zhou S，et al.Numerical investigation on galloping of iced quad bundle conductors［J］.IEEE Transactions on Power Delivery，2012，27(2):784-792.

［12］People’s Republic of China Electric Power Industry Standard.Technical code for designing 110～500 kV overhead transmission line［S］.DL/T 5092-1999P.(in Chinese)中华人民共和国电力行业标准.110～500 kV架空送电线路设计技术规程［S］.DL/T 5092-1999P.

［13］Barbieri N，Honorato de Souza O Jr，Barbieri R.Dynamic analysis of transmission line cables［M］.Part I-linear theory，Mechanical Systems and Signal Processing，2004，18:659-669.

［14］Barbieri N，Honorato de Souza O Jr，Barbieri R.Dynamic analysis of transmission line cables［M］.Part II-damping estimation，Mechanical Systems and Signal Processing，2004，18:671-681.

［15］Yan B，Lin X S，Luo W，et al.Numerical study on dynamic swing of suspension insulator string in overhead transmission line under wind load［J］.IEEE Transactions on Power Delivery，2010，25 (1):248-259.

W ake-induced galloping of eight bundle conductor lines

Yan Bo1，2，*，Cai Mengqi1，He Xiaobao1，Zhou Linshu1
(1.College of Aerospace Engineering，Chongqing University，Chongqing 400044，China;2.State Key Laboratory of Transmission＆Distribution Equipment and Power System Safety and New Technology，Chongqing University，Chongqing 400044，China)

Wake-induced galloping is a high risk for a safe operation of electrical transmission system due to dense arrangement of sub-conductors in multi-bundle conductors.To investigate the wakeinduced galloping characteristics of eight bundle conductors with extra-high voltage，the variation of aerodynamic forces of each sub-conductor in the eight bundle conductors changing with angle of attack was tested by wind tunnel tests.Because of the wake interaction within sub-conductors，a relatively distinguishable difference can be observed among the aerodynamic forces of the eight conductors.Especially，when a leeward sub-conductor is in the wake of windward sub-conductor，the drag exerted on the leeward conductor significantly drops.The wake-induced galloping of eight bundle conductors with two span-lengths 308 m and 405 m was numerically simulated by the ABAQUS software.Based on the simulation results，a critical wind speed has been found for the wake-induced galloping.The galloping will not take place when the wind speed is lower than the critical speed.The motion orbit of the subconductor is elliptical with wake-induced galloping.Given the same wind speed，the amplitude of the galloping with long span-length is greater than that with short span-length.

eight bundle conductor;aerodynamic characteristics;wake-induced galloping; numerical simulation

V211.3

A

10.7638/kqdlxxb-2014.0126

0258-1825(2016)05-0680-07

2015-02-06;

2015-05-20

国家自然科学基金(51277186)

严波*(1965-)，男，博士，教授，主要从事工程力学研究.E-mail:boyan@cqu.edu.cn

严波，蔡萌琦，何小宝，等.特高压八分裂导线尾流驰振研究［J］.空气动力学学报，2016，34(5):680-686.

10.7638/kqdlxxb-2014.0126 Yan B，Cai M Q，He X B，et al.Wake-induced galloping of eight bundle conductor lines［J］.Acta Aerodynamica Sinica，2016，34(5):680-686.