存在烧蚀的高超声速压缩拐角流动数值研究

葛明明，曾明，王东方，柳军

(国防科学技术大学航天科学与工程学院，湖南长沙410073)

存在烧蚀的高超声速压缩拐角流动数值研究

葛明明，曾明*，王东方，柳军

(国防科学技术大学航天科学与工程学院，湖南长沙410073)

耦合求解热化学非平衡流控制方程和烧蚀壁面边界条件，进行存在石墨烧蚀的压缩拐角流场数值模拟。流场化学反应采用16组元(N2，O2，NO，N，O，NO+，N2+，O+，N+，CO，CO2，C，C2，C3，CN，e－)29个反应的非平衡模型，热力非平衡的双温度模型下，不同反应采用不同控制温度。石墨材料表面反应包括碳的氧化反应、碳催化的O原子复合反应和碳的升华反应。对15°、18°、24°压缩拐角模型，在自由流Ma=10～30，总焓值6～55 MJ/kg范围，分别进行无烧蚀的壁面催化与非催化条件和石墨烧蚀条件下的流场计算，分析各类条件下的流场结构、流动分离特性以及流场热化学参数分布特点，研究壁面条件对流动特性的影响。结果表明:流动分离可能性和分离区范围随着压缩拐角斜面倾角增大而增大，随来流马赫数增大而减小;相对于低壁温条件，无烧蚀的辐射平衡壁温和壁面烧蚀条件下流动分离区增大，斜面上压力、摩阻和热流峰值点也有所后移。

高超声速非平衡流;压缩拐角流动;烧蚀;数值模拟

0 引言

高超声速飞行器以7 km/s以上的速度再入大气层时，遭受强烈的气动加热，飞行器物面辐射平衡温度高达2 000K以上，无法使内部装置正常工作。为此再入飞行器表面多采用烧蚀材料并通过高温气体与物面材料发生的气固热化学反应和质量交换，吸收大部分气动加热能量，使飞行器内壁保持允许的温度［1］。烧蚀产物引射到气体边界层中，影响到流场的化学反应和热力学特性，并进一步影响飞行器的光电特性。关于战略弹头等钝头体烧蚀流场特性，国内外已开展了大量深入的工作［2-8］，取得了富有成效的结果。本文在前人研究基础上，将烧蚀流场的研究扩充到其他高超声速飞行器外形或部件模型。

对再入飞行器和吸气式高超飞行器而言，控制面和发动机进气道区域的流场是需要重点研究的，因为在这些区域很容易发生激波/边界层干扰，影响控制面的效率和发动机的性能［9］。这些区域的流动可以简化为平板后接压缩面的压缩拐角流动。平板边界层从平板区逐渐发展，在拐角前会受到压缩面产生的斜激波的干扰。如果该斜激波足够强，边界层会发生分离，并在拐角区域形成回流区。分离使边界层变厚且压缩来流，产生分离激波。在再附点附近，气流受到压缩面压缩产生一系列压缩波，这些压缩波汇聚成一道激波，和分离激波相互作用，影响到压缩面壁面特性。在高焓来流条件下，高温气体效应将会对流场中的波系和分离区产生影响［9］。本文重点研究存在烧蚀的压缩拐角流动特性。在自由流Ma=10～30，总焓值6～55 MJ/kg范围，对15°、18°、24°压缩拐角模型，分别进行无烧蚀的壁面催化与非催化条件和石墨烧蚀条件下的流场计算，分析各类条件下压缩拐角的流场特性和壁面条件的影响。

1 热化学模型

石墨材料表面上发生的反应主要有碳的氧化反应，碳催化的O原子复合反应和碳的升华反应(生成C，C2，C3)，具体反应式和速率常数确定详见文献［3］。据此可以得到表面反应生成的各组元净质量流率。

对存在石墨烧蚀的高温空气流场计算时，考虑16个组元，29个化学反应，详见表1。反应式中，催化物M1、M2、M3、M4、M5、M6为各反应的催化物，就是流场中的某些组元。对反应1～反应21，速率系数采用文献［10］给出的方法，其余反应采用文献［11］的方法计算。

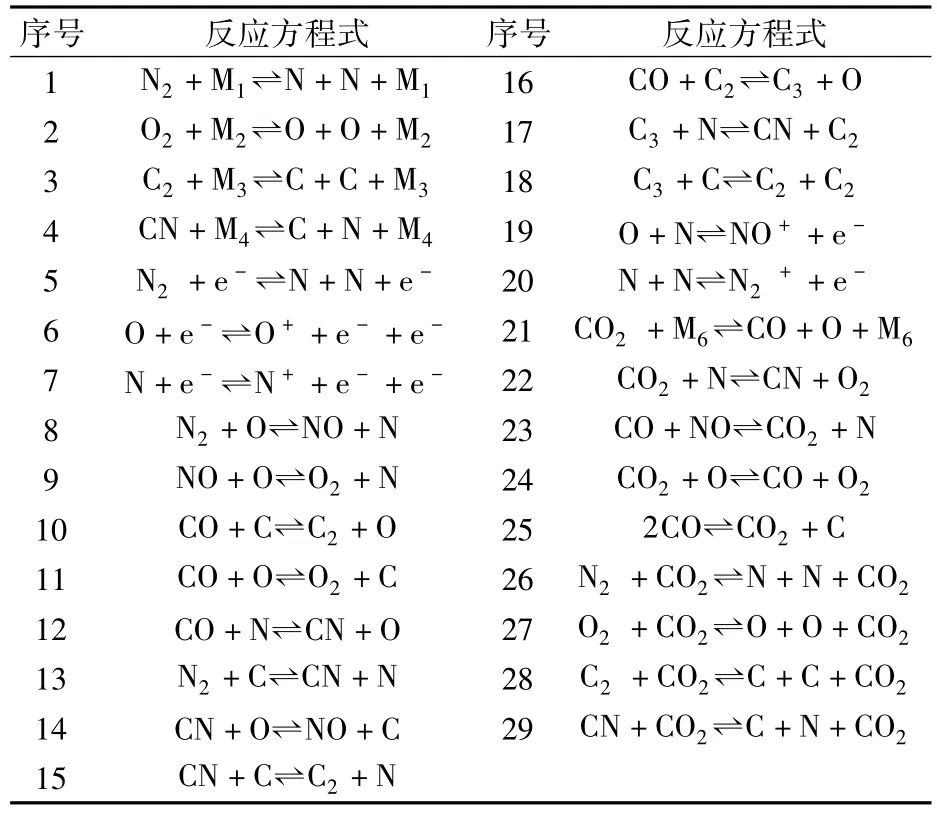
表1 流场化学反应Table 1 Chem ical reactions in the flow field

热力非平衡条件下，系统有两个温度，平动/转动温度T和振动温度Tv，振动松弛时间采用Park修正的Millikan和White振动松弛模型计算。双温度近似下，不同的反应采用不同的控制温度。气体热力学特性和输运特性的计算方法详见文献［10］。

2 流动控制方程与壁面边界条件

2.1 控制方程与计算方法

控制方程为时间相关的二维非平衡流N-S方程，求流场的定常解。无粘通量项采用AUSMPW+格式［12］离散，粘性项采用中心差分离散。流体力学方程和热化学动力学方程耦合求解时，采用全耦合隐式处理无粘通量项和源项，隐式处理方法为LU-SGS方法［13］。控制方程与求解的详细内容参见文献［14］。

2.2 烧蚀壁面边界条件与求解

壁面处s组元的质量平衡关系为

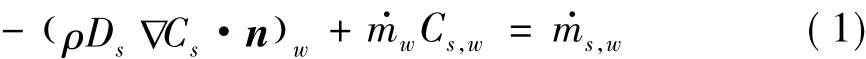
采用等离子体准中性假设后，可不含电子的质量平衡关系，式(1)共有15个方程。式中n为壁面单位法矢量，为由碳化表面反应产生的s组元的净质量流率，除组元O2、O、CO、C、C2、C3外，对其他组元为零。为壁面处总的质量流率，是表面反应产生的所有组元质量流率之和。

壁面的能量平衡关系为

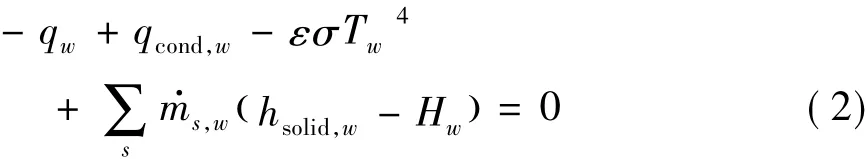
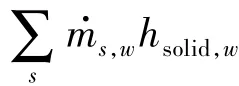
存在壁面质量引射时，壁面法向速度由总质量流率确定

上述方程中出现的壁面密度根据混合气体的状态方程确定，而壁面压力根据法向压力梯度为零确定。

联立求解各组元的壁面质量平衡关系式和壁面能量平衡关系式共16个非线性方程，即可确定壁面处的各组元质量分数和壁面温度。为求解方便，也可先假定壁温，求解质量平衡关系得到质量分数后再通过能量平衡关系式求解温度，之后进行迭代。非线性方程组的求解可采用牛顿迭代法。

另外，为对比分析壁面条件对流场特性的影响，本文还进行了三种无烧蚀壁面条件下的流场计算，分别是:等壁温(300K)的全催化和非催化条件，辐射平衡壁温的非催化条件。全催化壁面处质量分数为当地温度压力下的平衡值，非催化壁面处组元质量分数根据梯度为零确定。辐射平衡壁温根据能量平衡关系－qw=εσTw4确定。无烧蚀时壁面处速度为零。

3 计算结果与分析

3.1 计算程序的验证

作为对本文计算程序模拟存在激波/边界层干扰和流动分离的高超声速流场有效性的验证，作者曾对Holden［15］在Calspan 48-inch的激波风洞实验条件下的二维压缩拐角流场进行了计算。风洞自由流马赫数14.1、温度89K、密度5.27×10－4kg/m3，计算得到的压缩拐角壁面压强和热流分布与文献［16］给出的实验测量结果和计算结果一致，结果对比图详见文献［17］。作为对本文含烧蚀非平衡流场计算程序的验证，曾对再入条件(飞行速度10 km/s、高度65 km)下的球头石墨烧蚀流场进行计算，所得壁面热流等结果与文献［3］的计算结果一致性也较好，结果对比图详见文献［8］。

3.2 算例条件与计算网格

取上述的Holden在激波风洞中开展实验的二维压缩拐角实验模型(模型总长0.6096 m，其中前段平板长0.3048m;模型宽0.6096 m)。自由流密度设为风洞条件(5.27×10－4kg/m3)，但自由流温度设为300K，以体现高超声速流场的高温效应。在斜面倾角为15°、18°、24°三种情况下，分别计算了马赫数为10、14、20、30时的石墨烧蚀流场。作为对比，还进行了无烧蚀流场的计算，壁面分别设定为壁温300 K条件下的全催化壁、非催化壁、非催化辐射平衡壁温。

采用131×81(流向×法向)的网格。流向方向上，在头部、拐角处、压力峰值处均进行了加密。法向方向在壁面处进行了加密，第一层网格高度为6.096 ×10-5m，法向外边界与平板前缘产生的激波大致平行。具体网格布置如图1，图中网格进行了稀疏显示处理。

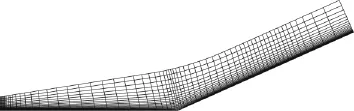
图1 计算网格Fig.1 Computational mesh

3.3 流场结构特点分析

高超声速压缩拐角流场中的波系结构如图2［17］。该图基于马赫数7.7条件下24°压缩拐角流场的压力等值线绘制。该条件下流动发生了分离，流场中除前缘激波和主激波外，还有较强的分离激波和再附激波。对未发生流动分离的情况，在拐角处前方，气流经过前缘激波后参数也已不均匀，斜面压缩在此产生的激波不再是斜激波，而是有一定的弯曲，且强度弱于主激波。这一段弯曲激波与流动分离时的再附激波作用类似，本文也将其命名为“再附激波”，方便后面的统一分析。前缘激波、分离激波、再附激波都可能穿透主激波或和主激波相交、融合，造成相交融合点附近的压力温度升高并引起峰值热流的急剧升高。具体的波系结构除了与自由流条件和压缩面角度有关，与拐角处平板的边界层状态也密切相关。

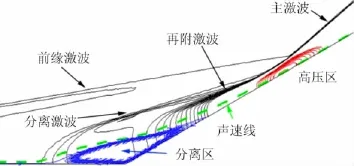
图2 压缩拐角流场结构示意图(24°拐角，Ma=7.7)［9］Fig.2 Flow field structure of a 24°com pression corner at Ma=7.7

本文诸自由流条件下，15°压缩拐角流动均未出现分离，18°压缩拐角流动仅Ma=10的烧蚀条件下有轻微分离，24°压缩拐角流动在Ma=30时无分离，在其它较小Ma均出现明显分离。这里以24°压缩拐角、Ma=14算例为代表，在图3中给出了全催化壁(用Cat.表示，壁温300K)和烧蚀条件下(Abaltion)流场的压强等值线和分离区流线。图4、图5分别给出了壁面压强系数和热流分布，图6给出了分离点附近的壁面摩阻分布。该算例流场化学反应微弱，等壁温条件下，壁面的催化特性对壁面热流和分离区范围都没有明显影响，烧蚀条件下的分离区范围比无烧蚀的辐射平衡壁温条件稍有增大。相对于低壁温条件，无烧蚀的辐射平衡壁温和壁面烧蚀条件下壁面热流有所降低。但流动的激波层增厚，分离区增大，这是高壁温导致边界层增厚从而影响激波形状及其与边界层相互作用特性的结果。分离特性的不同还将进一步影响到下游的流动特性，分离区增大后分离激波、再附激波与主激波相交于更远位置，斜面上压力、摩阻和热流峰值点均有所后移。

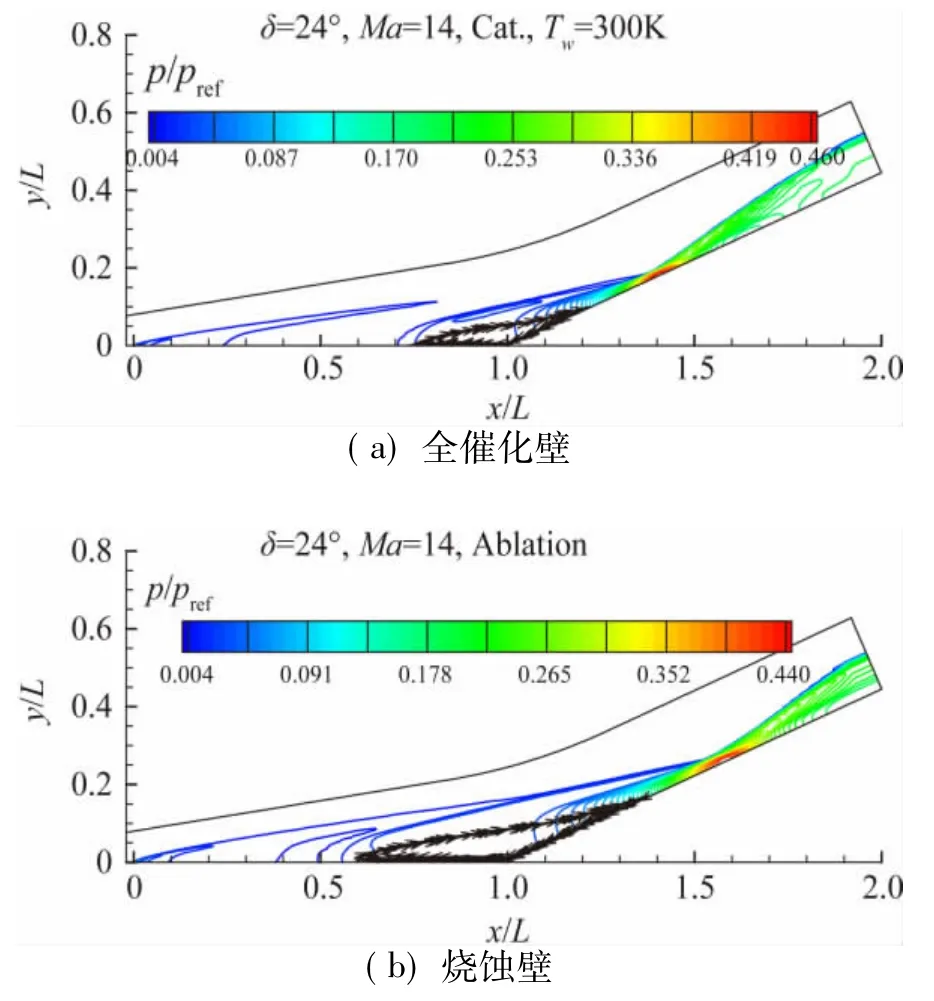
图3 Ma=14时24°压缩拐角流场压强分布与回流区流线Fig.3 Pressure distribution and stream line in recirculation zone at Ma=14

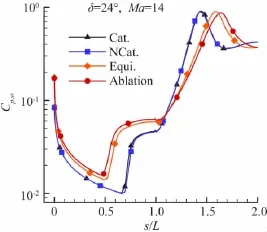
图4 Ma=14时24°压缩拐角壁面压强系数分布Fig.4 Surface pressure distribution at Ma=14

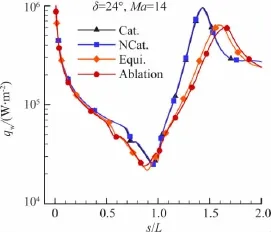
图5 Ma=14时24°压缩拐角壁面热流分布Fig.5 Surface heat transfer distribution at Ma=14

图6 Ma=14时24°压缩拐角分离点附近摩阻系数分布Fig.6 Friction distribution near the separation point at Ma=14

斜面倾角和壁面条件都相同的情况下，随着马赫数增大分离可能性减小。这是因为一方面马赫数增大后，压缩面形成的主激波激波角减小，激波更贴近物面，逆压梯度的范围减小;另一方面马赫数增大后边界层内的亚声速区范围也有所减小，逆压梯度向前传播的的范围也减小。马赫数越大，分离区越小，压缩面上压力峰值点越靠前。表2给出了24°压缩拐角流动存在分离的各算例的分离起始位置x/L，其中L为平板长度，x为离平板前缘距离。

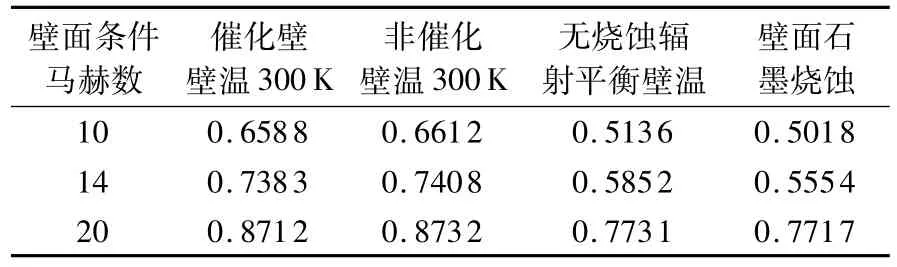
表2 24°压缩拐角流动分离起始位置x/LTab le 2 Start point of flow separation x/L

3.4 Ma=30时24°压缩拐角流场热化学参数分布

24°压缩拐角在Ma=30时的流场是激波最强、振动激发和化学反应也最强的情况。下面以24°压缩拐角在Ma=30、烧蚀壁面条件下流场热化学参数分布为例进行分析。图7给出了流场的压力等值线，图8分别给出了平动、振动温度等值线。由图8(a)可见在斜面前端出现高平动温度区，这是经过前缘激波压缩升温后的气流和拐角区较厚的边界层内升温了的气流，又经过“再附激波”的进一步压缩和升温所致。而由图7可见压力峰值区出现在主激波后，自由来流经过强主激波的压缩和升温，压力达到全场峰值，但由于自由来流温度较低(300 K)，温度仍低于“再附激波”后的气流。振动温度的峰值区在主激波后，这与振动激发随压力升高而加强有关。主激波较强的部分下游存在一条高温带，高温带中振动激发和化学反应明显要比周围流场剧烈，原子质量分数的高值区和振动温度的高值区范围接近。图9、图10分别给出了流场的O、NO+质量分数分布。

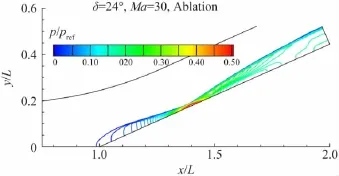
图7 Ma=30时24°压缩拐角流场压强分布Fig.7 Pressure distribution at Ma=30

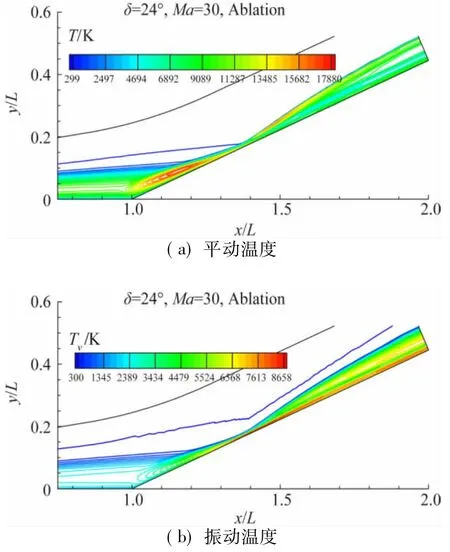
图8 Ma=30时24°压缩拐角流场平动与振动温度分布Fig.8 Translational temperature and vibrational tem perature distribution at Ma=30

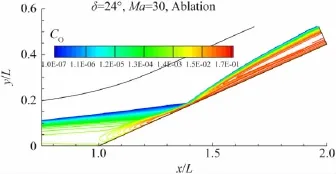
图9 Ma=30时24°压缩拐角流场O质量分数分布Fig.9 COdistribution at Ma=30

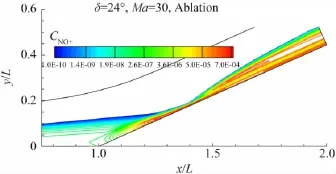
图10 Ma=30时24°压缩拐角流场NO+质量分数分布Fig.10 CNO+distribution at Ma=30

烧蚀产物基本上局限在边界层内，质量分数最高的烧蚀组元依次是CO、C3、C2、CN。图11、图12分别给出了CO、C3组元的质量分数分布。另外，C2质量分数峰值达到0.0574，CN值为0.0230，C峰值为0.0211，CO2峰值在10－3量级。烧蚀产物在接近拐角斜面尾部时达到峰值，图13给出了x/L=1.9时的烧蚀组元质量分数沿斜面法向分布。

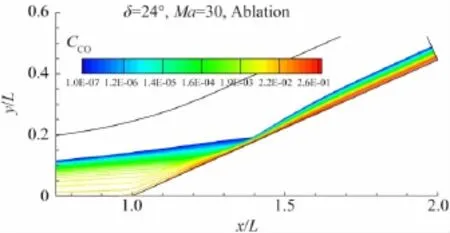
图11 Ma=30时24°压缩拐角流场CO质量分数分布Fig.11 CCOdistribution at Ma=30

图12 Ma=30时24°压缩拐角流场C3质量分数分布Fig.12 CC3distribution at Ma=30

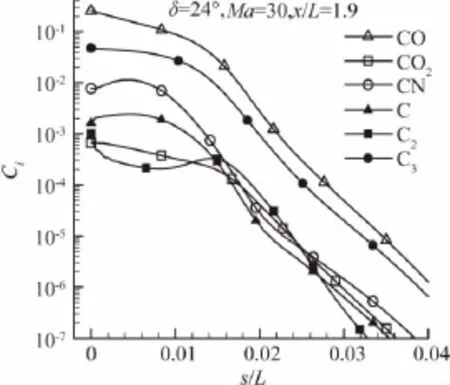
图13 Ma=30时24°压缩拐角流场烧蚀组元法向分布Fig.13 Ablation species normal distribution at Ma=30

图14给出了四种壁面条件下的壁面热流分布。相对于低壁温(300K)的催化和非催化条件，无烧蚀辐射平衡壁温和烧蚀条件下壁温有较大升高，所以拐角斜面上的热流有明显降低。其中低壁温条件下催化壁热流高于非催化壁，是因为算例条件下主激波后有较强的非平衡化学反应，催化壁条件下壁面处存在扩散热流。烧蚀条件热流又高于无烧蚀的辐射平衡壁温条件，也是因为烧蚀壁面处的放热化学反应。

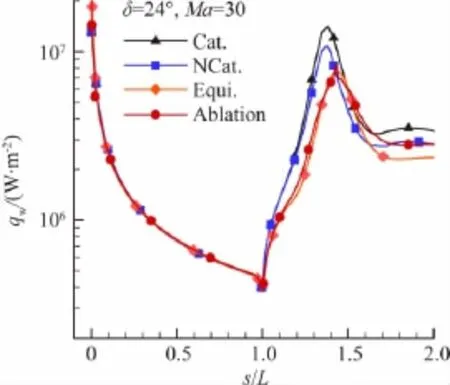
图14 Ma=30时24°压缩拐角壁面热流分布Fig.14 Distribution of surface heat flux at Ma=30

3.5 壁面条件对流场特性影响的分析

在3.3节中已知壁面条件对流场总体结构的影响特点。相对于低壁温条件，无烧蚀的辐射平衡壁温和壁面烧蚀条件下斜面上的热流率降低，但分离可能性和分离区范围增大，并且“再附激波”和主激波的相交位置后移，导致壁面压力和热流峰值区后移。无分离时的影响特点类似，但程度较小。

另外，无烧蚀的辐射平衡壁温和烧蚀条件下的激波层厚度和激波强度明显大于低壁温条件，并且烧蚀条件还比辐射平衡壁温条件下略大。这是壁温升高或烧蚀使边界层增厚，因而前缘激波和分离激波增强，激波也被推离物面所致。这里以斜面上压力峰值点位置为例，在图15、图16中给出了24°压缩拐角在Ma=14(存在流动分离)和Ma=30(无分离)条件下温度沿壁面法向的分布。斜面上压力峰值点位于再附激波和主激波相交区域。壁面条件不影响压力峰值，但高壁温条件下该处温度峰值更高;并且壁面条件的影响在存在流动分离的Ma=14算例上表现比无分离的Ma=30算例更明显。

由于激波层厚度的差异，低壁温和高壁温条件(无烧蚀的辐射平衡壁温和壁面烧蚀条件)下的组元分布也表现出相应的明显差异。不过无烧蚀的辐射平衡壁温和烧蚀两种壁面条件下组元分布差异主要体现在边界层内。烧蚀产物扩散到边界层内后进一步影响边界层内的化学反应和扩散，使高温空气的中性分子组元N2、O2增加，原子组元N、O和主要的离子组元NO+、N2+减少。图17、图18给出了斜面上压力峰值点处的N、NO、O组元和NO+、N2+组元质量分数沿法向分布，可以看出烧蚀的上述影响。

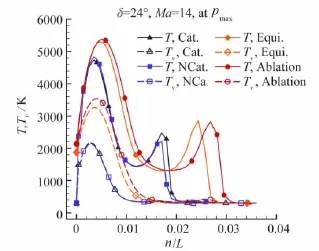
图15 Ma=14时24°压缩拐角斜面上压力峰值点处温度沿法向分布Fig.15 Normal distribution of temperature at pmaxat Ma=14

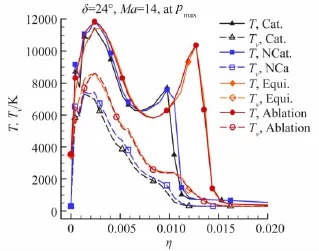
图16 Ma=30时24°压缩拐角斜面上压力峰值点处温度沿法向分布Fig.16 Normal distribution of temperature at pmaxat Ma=30

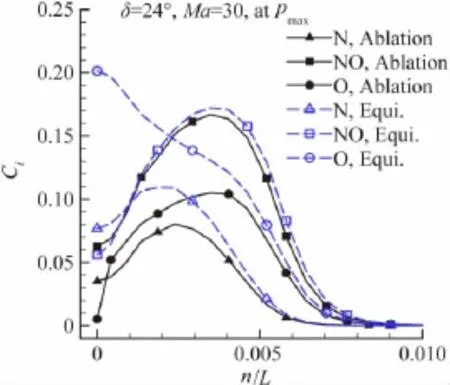
图17 Ma=30时24°压缩拐角斜面上压力峰值点处N、NO、O质量分数沿法向分布Fig.17 Normal distribution of CN，CNO，and COat pmaxat Ma=30

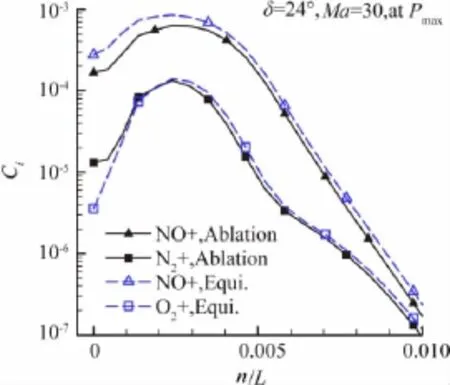
图18 Ma=30时24°压缩拐角斜面上压力峰值点处CNO+、CN2+质量分数沿法向分布Fig.18 Normal distribution of CNO+and CN2+at pmaxat Ma=30

4 结论

本文对15°、18°、24°压缩拐角模型，在自由流Ma =10～30，总焓值6～55MJ/kg范围，采用16组元双温度模型进行了无烧蚀和石墨烧蚀条件下的流场计算，得到如下结论:

1)压缩拐角处主激波后升压在壁面附近的边界层内前传，一定条件下逆压梯度可能导致平板边界层分离。随着压缩拐角度数增大激波增强，分离可能性增大。虽然自由流马赫数升高导致边界层增厚，但压缩面的主激波角变小，激波更贴近物面，分离可能性减小。本文15°和18°压缩拐角流动未出现分离，而存在分离的24°压缩拐角流动，随着马赫数升高分离区减小。

2)相对于低壁温条件，无烧蚀的辐射平衡壁温和壁面烧蚀条件下壁面热流有所降低。但流动的激波层增厚，分离区增大，这是高壁温导致边界层增厚从而影响激波形状及其与边界层相互作用特性的结果。分离特性的不同还将进一步影响到下游的流动特性，斜面上压力、摩阻和热流峰值点均有所后移。可见对这类存在较强激波-边界层相互作用的流动，壁面条件对流动特性的影响要远大于球头、球锥等外形。

3)壁面烧蚀产物扩散到边界层后进一步影响边界层内的化学反应和扩散。相对于无烧蚀的辐射平衡壁温条件，烧蚀条件下边界层内高温空气的中性分子组元含量有所升高，原子和离子组元含量则有所下降。不过这两种壁面条件下的流场结构和边界层外流动特性没有明显差异，烧蚀的影响基本局限于边界层内。

本文针对准定常烧蚀流场，亦即壁面温度最高、烧蚀产物含量最大的情况下开展烧蚀对流场特性的影响研究，比较具有代表性。考虑到不同壁温条件下烧蚀产物组成不同，非定常过渡过程中烧蚀对流场特性的影响会有不同表现。进一步的工作需要耦合固体热传导方程，针对非定常烧蚀流场开展详细研究。

［1］Le Jialing，Gao Tiesuo，Zeng Xuejun.Reentry physics［M］.Beijing:National Defense Industry Press，2005.(in Chinese)乐嘉陵，高铁锁，曾学军，等.再入物理［M］.北京:国防工业出版社，2005.

［2］Keenan J A，Candler G V.Simulation of ablation in Earth atmosphere entry.AIAA-93-2789［R］.Reston:AIAA，1993.doi:10.2514/6.1993-2789.

［3］Keenan J A，Candler G V.Simulation of graphite sublimation and oxidation under re-entry conditions.AIAA-94-2083［R］.Reston: AIAA，1994.doi:10.2514/6.1994-2083.

［4］Suzuki K，Kubot H，Fujita K，et al.Chemical nonequilibrium ablation analysis of MUSES-C super-orbital reentry capsule.AIAA-97-2481［R］.Reston:AIAA，1997.doi:10.2514/6.1997-2481.

［5］Gao T S，Dong W Z，Zhang Q Y.The computation and analysis for the hypersonic flow over reentry vehicles with ablation［J］.Acta Aerodynamica Sinica，2006，24(1):41-45.(in Chinese).高铁锁，董维中，张巧芸.高超声速再入体烧蚀流场计算分析［J］.空气动力学学报，2006，24(1):41-45.

［6］Tissera S，Titarev V，Drikakis D.Chemically reacting flows around a double-cone including ablation effects.AIAA 2010-1285［R］.Reston:AIAA，2010.doi:10.2514/6.2010-1285.

［7］Bianchi D，Nasuti F，Onofri M.Aerothermodynamic analysis of reentry flows with coupled ablation.AIAA 2011-2273［R］.Reston: AIAA，2011.doi:10.2514/6.2011-2273.

［8］Zhang W，Zeng M，Xiao L F，et al.Numerical study for the effects of ablation and pyrolysis on the hypersonic reentry flow［J］.Journal of National University of Defense Technology，2014，36(4):41-48.(in Chinese) doi:10.11887/j.cn.20140400.张威，曾明，肖凌飞，等碳-酚醛材料烧蚀热解对再入流场特性影响的数值研究［J］.国防科技大学学报，2014，36(4):41-48.

［9］Mallinson S G，Gai S L，Mudford N R.High enthalpy，hypersonic compression corner flow［J］.AIAA Journal，1996，34(6):1130-1139.doi:10.2514/3.13202.

［10］Park C，Jaffe R L，Partridge H.Chemical-kinetic parameters of hyperbolic Earth entry［J］.Journal of Thermophysics and Heat Transfer，2001，15(1):76-90.doi:10.2514/2.6582.

［11］Blottner F G.Prediction of electron density in the boundary layer on entry vehicles with ablation［R］.N71-21113，1971.

［12］Kim K H，Kim C，Rho O H.Accurate computations of hypersonic flows using AUSMPW+scheme and shock-aligned grid tehnique.AIAA-98-2442［R］.Reston:AIAA，1998.doi:10.2514/6.1998-2442.

［13］Stoll P，Gerlinger P，Bruggermann D.Domain decomposition for an implicit LU-SGS scheme using overlapping grids.AIAA-97-0770［R］.Reston:AIAA，1997.doi:10.2514/6.1997-0770.

［14］Zeng M.Numerical rebuilding of free-stream measurement and analysis of nonequilibrium effects in high-enthalpy tunnel［D］.Beijing:Institute of Machanics，CAS，2007.(in Chinese)曾明.高焓风洞流场测量的数值重建与非平衡效应的数值分析［D］.北京:中国科学院力学研究所，2007.

［15］Holden M S，Moselle J.Theoretical and experimental studies of the shock wave-boundary layer interaction on compression surfaces in hypersonic flow［R］.ARL 70-0002，1970.

［16］Rudy D H，Thomas J L，Kumar A.Computation of laminar viscousinviscid interactions in high-speed internal flows［R］.N 91-21087，1991.

［17］Wang D F.Study of hypersonic viscous intereaction including hightemperature gas effects［D］.Changsha:National University of Defense Technology.2011.(in Chinese)王东方.高超声速非平衡粘性相互作用研究［D］.［硕士学位论文］.长沙:国防科学技术大学，2011.

Numerical study for the hypersonic com pression corner flow w ith ablation

Ge Mingming，Zeng Ming*，Wang Dongfang，Liu Jun
(College of Aerospace Science and Engineering，National University of Defense Technology，Changsha 410073，China)

Hypersonic flow over a compression corner with ablation of heat shield made of graphite is numerically simulated through solving the Navier-Stokes equations of thermochemical nonequilibrium flow coupled with the ablating boundary condition，and the effects of the wall conditions on the flowfield properties are investigated.Sixteen chemical species(N2，O2，NO，N，O，NO+，N2+，O+，N+，CO，CO2，C，C2，C3，CN，e－)are considered，the two-temperature model is taken to describe thermal nonequilibrium.The oxidation and sublimation of C，as well as the recombination of O catalyzed by C are considered at the wall surface.The hypersonic flow over 15°，18°，24°compression corners are calculated with Mach number varied from 10 to 30 and total enthalpy from 6 to 55MJ/kg.Both ablating and non-ablating surface condition are used to investigate the effects of ablation.The flow structure，the characteristics of shock—boundary-layer interaction，the separation properties，and the distribution of the thermochemical properties are analyzed.The results show that the possibility of flow separation and the separation range become larger as the corner angle increases，while smaller as the free stream Mach number rises.Compared with the cases with low-temperature wall，the flow separation zones are lager with ablating wall or with high-temperature wall in radiation equilibrium，and this leads to the positions for peak values of pressure，skin friction and heat flux move downstream.

hypersonic nonequilibrium flow;compression corner flow;ablation;numerical simulation

V211.3

A

10.7638/kqdlxxb-2015.0033

0258-1825(2016)05-0666-08

2015-03-18;

2015-05-08

国家自然科学基金项目(11102231，11572348)

葛明明(1991-)，男，江苏南通人，博士，研究方向:计算流体力学.E-mail:owen2024@sina.cn

曾明*(1971-)，女，湖南娄底人，博士，副教授，研究方向:高超声速与高温气体动力学.E-mail:ming_z@163.com

葛明明，曾明，王东方，等.存在烧蚀的高超声速压缩拐角流动数值研究［J］.空气动力学学报，2016，34(5):666-673.

10.7638/kqdlxxb-2015.0033 Ge M M，Zeng M，Wang D F，et al.Numerical study for the hypersonic compression corner flow with ablation［J］.Acta Aerodynamica Sinica，2016，34(5):666-673.