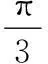高二数学测试



高二数学测试

一、填空题(本大题共14小题,每小题5分,共70分)

1.命题“∀x>1,x2>1”的否定是______.

2.等轴双曲线的两渐近线的夹角为______.

3. “x>3”是“x≥2”的______条件(从“充分不必要”、“必要不充分”、“充要”或“既不充分又不必要”中选一个填空)

4.椭圆mx2+y2=1的一个焦点坐标为(1,0),则实数m的值为______.

7.已知圆C经过A(5,2),B(-1,4)两点,且圆心在x轴上,则圆C的方程为______.

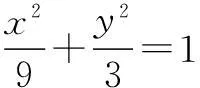
9.已知圆x2+y2=4上存在两点到点(m,m)(m>0)的距离为1,则实数m的取值范围为______.

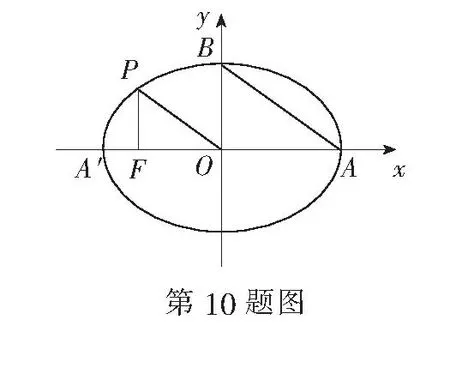
10.如图,A,A′,B分别是椭圆顶点,从椭圆上一点P向x轴作垂线,垂足为左焦点F,且AB∥OP,则椭圆的离心率为______.

11.已知抛物线y2=4x上一点P在y轴上的射影为N,动点M在直线y=x+2上,则PM+PN的最小值为______.

12.已知等边三角形ABC边长为4,动点P满足PA2+PB2=12,则线段PC长度的取值范围是______.

14.已知M,N为y轴正半轴上的两个动点,点P(异于原点O)为x轴上的一个定点.若以MN为直径的圆与圆(x-3)2+y2=4相外切,且∠MPN的大小恒为定值,则线段OP的长为______.

二、解答题(本大题共6小题,共90分. 解答应写出文字说明、证明过程或演算步骤.)

15.(本小题满分14分)已知命题p:方程x2+y2+2ax+a=0表示圆;命题q:方程ax2+2y2=1表示焦点在x轴上的椭圆.若p∧q为假命题,求实数a的取值范围.

(1)弦AB的长; (2)∆F2AB的面积.

17.(本小题满分14分)已知直线l过定点P(1,0)且与圆C:(x-2)2+(y-2)2=4相交于A、B两点.

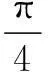
(2)求当∆ABC的面积最大时直线l的方程.

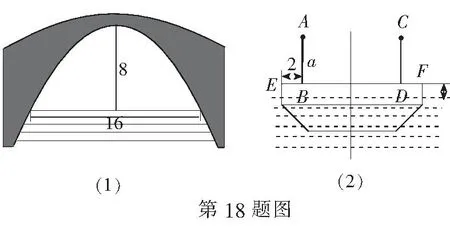
18.(本小题满分16分)如图(1),一座抛物线型拱桥,水面离拱顶8 m,水面宽16 m.如图(2),一艘船的宽度为12 m,船的甲板与水面距离为1 m,船上两根高为am的桅杆垂直于船的甲板,且到甲板左右两边的距离均为2 m. 现船正面正对桥洞(船截面的中轴线与抛物线对称轴重合时)通过该拱桥.

(1)当a=3时,该渔船是否能安全通过该拱桥?

(2)若该渔船能安全通过该拱桥,求a的最大值.

(1)求椭圆C的方程;

(2)已知直线l:x=1与椭圆C交于P、Q两点,点M为椭圆C上一动点,直线PM,QM与x轴分别交于点R,S,求证:|OR|·|OS|为常数(O为原点),并求出这个常数.

(1)求椭圆C的方程;

(2)如图,点M,N为椭圆C上相异的两点,其中点M在第一象限,且直线AM与直线BN的斜率互为相反数.

① 证明:直线MN的斜率为常数;

② 求四边形AMBN面积S的取值范围.

参考答案

一、填空题

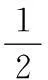
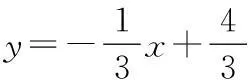
二、解答题

15.命题p等价于“a<0或a>1”,

命题q等价于“0

∵p∧q为假命题,

∴a≤1或a≥2.

根据几何意义,CM⊥l,所以CM所在直线方程为y=-x+4.

=2sin∠ABC.

① 当直线l斜率不存在时,不符题意,舍去；

② 当直线l斜率存在时,设直线l的方程为y=k(x-1),则

18.(1)以拱顶为原点、水平方向为x轴建立直角坐标系,抛物线过点(8,-8),则抛物线方程为x2=-8y.

当a=3,正面通过桥洞时,点C坐标为(4,-4),点F点坐标为(6,-7).

对于抛物线,当x=4时,y=-2>-4,所以C点能安全通过,

根据对称性,点A、E均能安全通过,所以,该渔船能安全通过该拱桥.

(2)由(1)可得,当x=4时,y=-2,所以a的最大值为-2-(-7)=5.

答 (1)当a=3时,该渔船能安全通过该拱桥;

(2)若该渔船能安全通过该拱桥,a的最大值为5.

19.(1)根据题意,AF1+AF2=6,AF1=2AF2,所以AF1=4,AF2=2.

(2)设点M的坐标为(x0,y0),

令y=0,则点P横坐标为

所以|OR|·|OS|

|OR|·|OS|=9.

(2)①∵直线AM与直线BN斜率互为相反数,

∴设直线AM方程为x=my+2,

记A、B到直线MN的距离分别为dA、dB,则

x2+2bx+2b2-2=0,

SAMBN=S∆AMN+S∆BMN