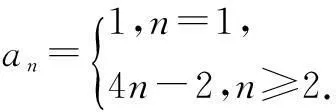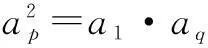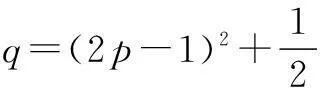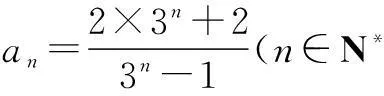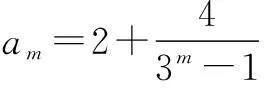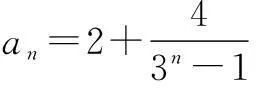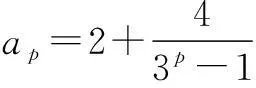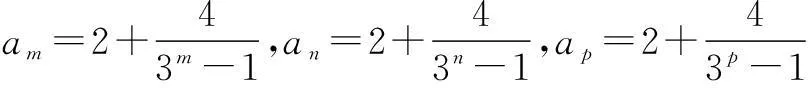数列中的存在性问题



数列中的存在性问题

施磊静

(江苏省如皋市第一中学，226500)

根据目前高考说明,数列这一章节等差数列和等比数列都是C级要求,所以数列的解答题在每次高考试题中都会出现. 数列中的存在性问题,因其独特的规律性和探究性,在考查学生分析问题、解决问题能力方面,具有很好的甄别功能,因此备受命题人青睐.本文就有解型和无解型两类问题例说如下.

一、有解型问题

数列中的存在性问题其实是数学探究中的一种形式,而数列具有它的特殊性,就是寻求整数解问题.对有解型问题，整数解可以通过枚举,关键是利用值域要找到枚举的范围.

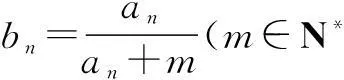
(1)若b1,b2,b8成等比数列,试求m的值;

(2)是否存在m,使得数列{bn}中存在某项bt满足b1,b4,bt(t∈N*,t≥5)成等差数列?若存在,请指出符合题意的m的个数;若不存在,请说明理由.

解(1)∵Sn=n2,

∴当n≥2时,an=Sn-Sn-1=2n-1.

又当n=1时,a1=S1=1,适合上式,

∴an=2n-1(n∈N*)，

由b22=b1b8,得

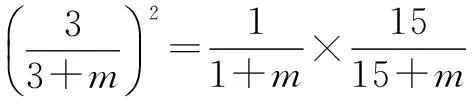
解得m=0(舍)或m=9,所以m=9.

(2)假设存在m,使得b1,b4,bt(t∈N*,t≥5)成等差数列,即2b4=b1+bt,则

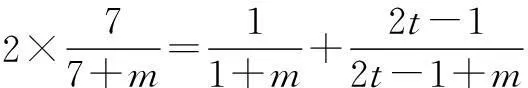
所以当m-5=1,2,3,4,6,9,12,18,36时,分别存在t=43,25,19,16,13,11,10,9,8适合题意,即存在这样m,且符合题意的m共有9个.

评注本题属于值域法中的约数型,这是有解问题中比较简单的一种类型.本题关键是要找到枚举的范围,所以我们把具有整数特征字母表示出来,若分式较复杂,可以先简化分子,然后通过两边都是整数得到枚举的范围.

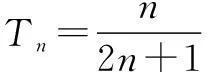
分析假设存在正整数m,n(1

评注本题的解题关键依然是寻求枚举的范围,和上一题有区别,我们把此题简称为值域法中的范围型.通过解不等式来确定枚举范围从而解决问题.

二、无解型问题

例3数列{an}的前n项和为

Sn=2an-3n(n∈N*).

(1)若数列{an+c}成等比数列,求常数c的值;

(2)求数列{an}的通项公式an;

(3)数列{an}中是否存在三项,它们可以构成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.

解(1)由Sn=2an-3n及Sn+1=2an+1-3 (n+1)，两式相减，得an+1=2an+3,

∴c=3时{an+3}成等比数列.

(2)S1=2a1-3⟹a1=3,由(1)知,an+3=(a1+3)·2n-1,an=3·2n-3,n∈N*.

(3)设存在s,p,r∈N*,且s

2 (3·2p-3)=(3·2s-3)+(3·2r-3)，

∴2p+1=2s+2r，

∴2p-s+1=1+2r-s.

∵s,p,r∈N且s

∴2p-s+1、2r-s为偶数,1+2r-s为奇数,

故2p-s+1=1+2r-s不可能成立,

故不存在满足条件的三项.

评注本题第(3)问三个变量,通过两边同除以2s将三个变量转变为了两个整体,而且使式子有较明显的特征：一边是奇数一边是偶数,从而得到不存在满足条件的三项,本题也告诉我们化繁为简的重要性.

例4已知数列{an}的前n项和

Sn=2n2-1.

(1)求数列{an}的通项公式;

(2)是否存在正整数p，q(p>1且q>1)使a1，ap，aq成等比数列?若存在,求出所有这样的等比数列;若不存在,请说明理由.

解(1)∵Sn=2n2-1,

∴a1=S1=1.

当n≥2时,

an=Sn-Sn-1=4n-2，

又a1=1不满足上式，

(2)假设存在正整数p、q(p>1且q>1)使a1、ap、aq成等比数列,则

∴(4p-2)2=1×(4q-2)，

∵p,q均为大于1的正整数,

∴左边是正数,而右边是分数,此等式不可能成立，∴假设错误,故不存在正整数p、q(p>1且q>1)使a1，ap，aq成等比数列.

若存在三项am,an,ap,使数列am,an,ap是等差数列,则

2an=am+ap,

化简得

3n(2×3p-n-3p-m-1)

=1+3p-m-2×3n-m.

(*)

因为m,n,p∈N*,m0,所以(*)式不可能成立.

故数列{an}中不存在三项am,an,ap,使数列am,an,ap是等差数列.

2×3m+p+2×3n=3n+p+3p+3m+3m+n.

两边同除3n，得

2×3m+p-n+2=3p+3p-n+3m-n+3m.

∵m

∴上式左边为整数，右边为分数，等式不可能成立.

故数列{an}中不存在三项am,an,ap,使数列am,an,ap是等差数列.

评注此题要求较高,解法1是通过求出了两边等式的最值,是从正负数角度挖出了矛盾；解法2从整数与分数的角度寻找矛盾，彰显了数学思维的灵活性.

上面这几个题型都是我们高中数列中存在性问题的最常见题型,也是高考考查重点.存在性问题一般可以从约数,范围角度确定枚举范围；而不存在问题主要是寻找矛盾,我们往往可以从推理的结论与题目条件公理定理找矛盾,也可以利用奇数与偶数,整数与分数,有理数与无理数,正数与负数来寻求矛盾.重要的是我们必须通过解题教会学生思维,让学生从各种题型中辨析中提炼解题思想,从而提高学生的解题能力.