挖掘数学本质 游刃数学解题——从高三数学习题评讲课说起



挖掘数学本质游刃数学解题
——从高三数学习题评讲课说起

秦志伟

(江苏省天一中学，214101)

高三复习阶段,免不了有很多的数学习题评讲课．习题评讲课上,教师首先要解决本班学生在这些习题上出现的主要问题,其次要通过这些习题,对零碎的知识点加以梳理和整合,以期学生的学科知识能趋于系统化．随着复习的深入,学生对基础知识的掌握日趋牢固,对知识的系统化理解日趋完善,在此阶段,笔者认为,教师的教学侧重点可以倾向于数学问题的优化解决、问题的本质探寻和问题的多角度解决．这样做,一方面能持续引起学生的学习兴趣,另一方面能引导学生注重对数学问题的本质进行探究，从而提升学生的思维品质．

笔者结合本人高三教学习题评讲课上的几个案例,以期说明数学问题的更好解决有赖于对数学问题的本质探寻．

一、数学解题有赖于充分理解数学概念

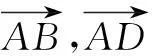
生2:我的思路跟生1差不多,只是我是建系之后用坐标算的．

教师此时结束讨论,对三个学生都加以肯定,尤其肯定生3的做法,继而强调数学的学习尤其要注重对数学概念的理解．

我们发现这个题目本身不难,但是它有评讲的价值,因为借助于这个题目我们的教学能达成多个目的．首先,复习了向量问题的两种基本的解决思路——基底法和坐标法;其次,利用向量数量积的定义能大大优化算法;最后,通过这个具体的例子,让学生意识到充分理解数学概念,有利于挖掘数学的本质．

上习题课前,教师首先应评估题目的价值,评估的依据不是正确率也不是难度,而是这个题目能给学生带来什么样的启示．题目,仅仅是一个载体,它应承载着搭建系统化的知识网络、启迪学生更有效的思考和传递教师的良好倡导等使命．教师利用题目,引导学生对数学概念加以充分理解就是一个不错的导向．数学,本身就是一门注重概念的学科,数学的建构完全依赖于一个一个明确的概念．所以,对数学概念的充分理解往往能从本质上抓住解决数学问题的关键所在．

二、数学解题有赖于深刻领悟数学思想

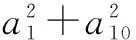
课上两位同学在黑板上展示了各自的解法:

生4:设{an}的公差为d,由题意，知

(*)

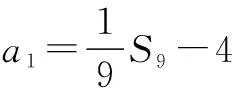
教师让其余学生对黑板上的两种解法进行评价，学生一致认为生5的整体换元法简洁．教师不失时机的指出数列基本量的相对性保证了这种整体换元的可行性，学生表示很认同．

这个问题的解决,整体化思想的使用固然巧妙,但深层次的原因则是基底化思想的使用．确定一个等差数列需要两个量,可以是基本量也可以是其他量,等差数列的问题可以转化为用两个基本量来表示,也可以转化为用其他两个量来表示(案例2中用了a1,a10这两个量)．利用这种相对性,生5的方法就不难想到了，这种思想与向量基底的不唯一性是相通的,我们姑且将其叫做基底化思想．

习题课上让不同的学生展示不同的解法,通过对解法的比较,学生能深刻感受到问题的解决是如何被优化的,以及优化的深层原因正是对数学思想方法的深刻领悟．数学,是一门注重理性思维的学科,其中的数学思想方法更是理性思维的精华所在,而数学的本质也往往与这些思想方法相结合,所以,很多情况下深刻领悟数学思想与发掘数学本质是一致的．数学思想方法的教学不可能一蹴而就,它应该始终贯穿于数学的教学之中.尤其在习题课上,教师更应该不失时机的利用具体的习题,让学生切实感受到运用思想挖掘本质的过程．

三、数学解题有赖于积极转变数学视角

这个习题是上一节课的思考题,教师用实物投影的方式展示了两位学生的解法．

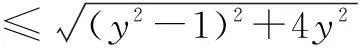
y2-4y+1≤0，

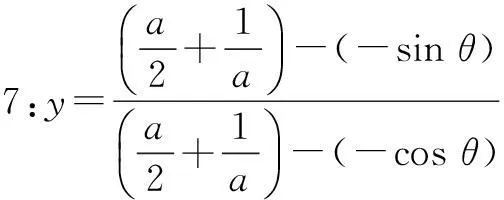
教师对两种解法均给予高度肯定,并追问求双变量函数的最值还有哪些常用处理手段,由此引出这节习题课的一个主题．

这个案例是习题课上就一个主题讨论前的引例.之所以选择它,一方面是作为作业的反馈,肯定了学生的变现,另一方面这两种方

法都有一个共同点,即实现了两个变量a,θ的分离,这样就有便于我们逐个变量分析、研究．更深层次的目的,是为了引发学生就双变量函数最值问题的解决方法的讨论．

我们常常要求学生解题要灵活,学生的灵活性不仅依赖于其全面的知识体系，更依赖于其发散的思维．习题评讲课就可以借助典型题目,通过一题多解,以期概括一类问题的解决方法并启迪学生发散的思维．对数学的理解本身就有不同的方式,比如一条直线,我们既可以从形上来认识它,也可以通过它的方程来研究它;比如一个代数式,我们既可以赋予其一定的几何意义,也可以通过函数来研究它．问题的本质只有一个,但我们可以用不同的方式来理解本质,这样就会形成不同的解决方法．经常有针对性的在习题评讲课上设计一题多解,可以帮助学生从不同的角度理解数学的本质,从而找到最优化的方法,同时也启迪其发散思维．

数学问题的完美解决有赖于对数学问题本质的挖掘,而数学本质的挖掘又有赖于对数学概念的充分理解、对思想方法的深刻领悟以及积极地转变数学视角．教师充分利用习题评讲课,通过一个个具体例子,采取不同的教学方式,如讨论、展示或比较等,与学生一起经历挖掘本质的过程．如此,能使高三习题评讲课真正走上高效之路;如此,既能在高三阶段持续激发学生学习的兴趣,也能启迪更深刻和更发散的思维．