从函数变换的视角解题



○短文集锦○

从函数变换的视角解题

樊陈卫

(江苏省海门中学，226100)

函数图象的变换规律揭示了同族函数之间的联系,掌握函数图象的变换规律,可以很好地帮助我们作出函数简图,把握函数图象的本质特征.而函数图象的变换规律的应用却不止于此,对一些函数问题若从函数变换的角度去思考,往往能化繁为简,获得较好解题方法,下面举例说明.

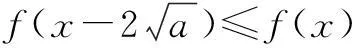
解由已知

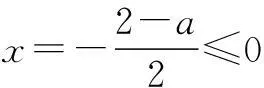
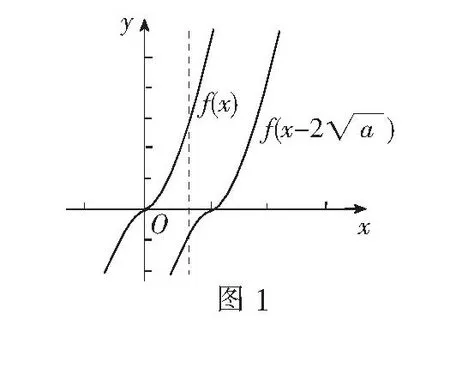
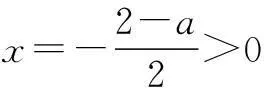
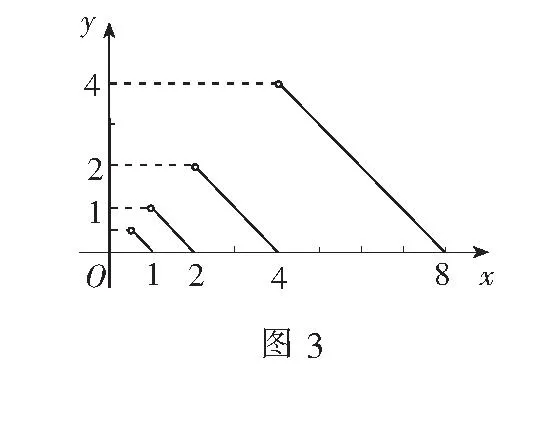
例2(2010年福建高考题)已知定义域为(0,+∞)的函数f(x)满足:(1)对任意的x∈(0,+∞),恒有f(2x)=2f(x)成立;(2)当x∈(1,2]时,f(x)=2-x．给出的如下结论:① 对任意m∈Z,有f(2m)=0；② 函数f(x)的值域为[0,+∞)；③ 存在n∈Z使得f(2n+1)=9；④ “函数f(x)在区间(a,b)内递减”的充要条件是“存在k∈Z,使得(a,b)⊆(2k,2k+1).其中所有正确结论的序号是______.

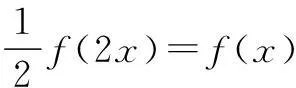
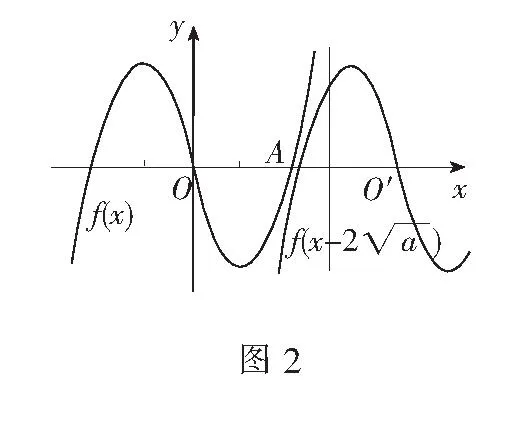
例3若方程2xlog2x+x·2x+xlog2x+x2=0的两根分别为α,β,则α+β=______.

解原方程可化为(2x+x)(log2x+x)=0.不妨设2x+x=0的根为α,α为y=-x与y=2x的图象的交点A的横坐标;log2x+x=0的根为β,β为y=-x与y=log2x交点A′的横坐标.交换等式y=2x中变量x,y所得的函数x=2y(也即y=log2x)图象与原函数关于直线y=x对称,过原点的直线y=-x也关于直线y=x对称,所以A,A'关于原点对称,故α+β=0.

至此,读者可能会注意到,本文主旨从函数变换的视角分析思考问题,所针对的情形是条件中存在某个等式或不等式,式子中存在某个函数及其经过某种变换后的函数.把等式或不等式理解为这两个相关函数之间图象的某种关系,再从图象上去分析思考,就能获得比较简捷的解法.