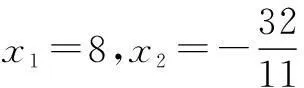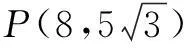例谈高中数学建模的常见类型



例谈高中数学建模的常见类型

蔡勇全

(四川省资阳市外国语实验学校，641300)

《普通高中数学课程标准》中明确提出高中数学教学“要发展学生的数学应用意识”,要“开展‘数学建模”的学习活动”,“促进学生逐步形成和发展数学应用意识,提高实践能力”.可见,数学建模已被提高到一定的高度,但是学生在数学建模中,最难的是如何分析出实际问题所涉及到的数学模型.下面就高中数学建模中的常见模型予以举例说明,供大家参考.

一、函数模型

例1根据统计资料,我国能源生产自1985年以来发展速度很快,下面是我国能源生产总量(折合亿吨标准煤)的几个统计数据：1985年8.6亿吨,1990年10.4亿吨,1995年12.9亿吨.有关专家预测，到2005年我国能源生产总量将超过20亿吨.试给出一个简单模型,说明有关专家的预测是否合理.

分析这是一个能源总量随着年份变化的定量分析问题,可以考虑用“函数”作模型.

解为方便起见,把已知 的三组数据(1 985,8.6),(1 990,10.4),(1 995,12.9)变换为(0,8.6),(5,10.4),(10,12.9),用图象或代数方法易见不适合用一次函数对数据拟合，试选用二次函数拟合.令相应的二次函数为y=ax2+bx+c,以变换后的三组数据代入，得

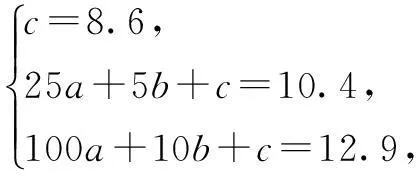
所以y=0.014x2+0.29x+8.6,对应于2005,取x=20,代入此函数关系式得y=20,这说明有关专家的预测合理.

二、方程模型

例2某顾客第一次在商店买x件商品花去y元,第二次再去买该商品时,发现这种商品已降价,且120件正好降80元,因此这一次他比第一次多买10件,共花去20元.若该顾客第一次至少花去10元,那么他第一次至少买商品多少件?

分析容易看出,这个问题涉及方程，可用“方程”模型.

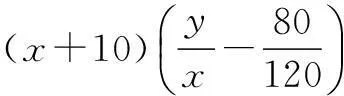
解之得x≥5或x≤-30(舍去),所以该顾客第一次至少买5件商品.

三、不等式模型

例3汽车在行驶过程中,由于惯性作用,刹车后还要继续向前滑行一段距离才能停住,我们称这段距离为“刹车距离”.刹车距离是分析事故的一个重要因素,在一个限速40 km/h以内的弯道上,甲、乙两辆汽车相向而行,发现情况不对,甲、乙两司机同时刹车,但还是碰车了.事发后现场测得甲车的刹车距离略超过12 m,乙车的刹车距离略超过10 m,又知甲、乙两种车型的刹车距离S(m)与车速x(km/h)之间分别有如下关系:S1=0.1x+0.01x2;S2=0.05x+0.005x2，问超速行驶应负主要责任的是谁?

分析要弄清主要责任者,应需分析行驶速度,要弄清速度问题,就要运用刹车距离函数和实测数据,构建一元二次不等式.

解S1=0.1x1+0.01x21>12,S2=0.05x2+0.005x22>10分别求解得:x1>30,或x1<-40(舍去);x2>40或x2<-50(舍去).经比较知乙车超过限速,应负主要责任.

四、数列模型

例4某地区位于沙漠边缘地带,人与自然进行了长期顽强的斗争,到2000年底,全地区的绿化率已达到30%,从2001年开始,预计将会出现以下变化,原有沙漠面积的16%栽上树,并成为绿洲;同时,原有绿洲面积的4%又被侵蚀为沙漠,问至少经过多少年的努力,才能使全地区的绿洲面积超过60%?(年数取整数,lg 2≈0.301 0)

分析这里涉及两个量的“连环关系”,分别用两个数列的递推公式去表示即可.设经过n年后绿洲面积为an+1,沙漠面积为bn+1,根据题意能较容易找出递推公式.

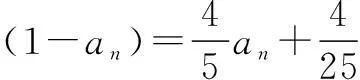
五、三角模型

例5如图1,某城市有一条公路从正西方通过市中心O后转向东北方OB,现要修筑一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,现要求市中心O与AB的距离为10千米,问把A、B分别设在公路上离市中心O多远处,才能使AB最短,并求其最短距离.

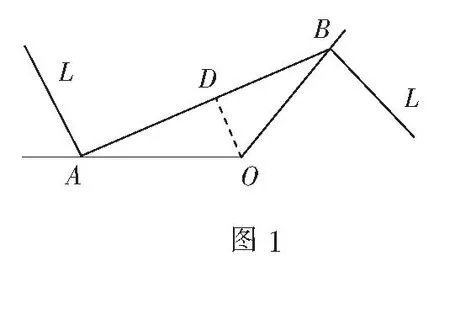
分析此题因为涉及到最值,并与直角三角形有关,可以建立“三角”模型来研究.

解过点O作OD⊥AB于点D,则OD=10.设∠DAO=α,则

AD=10cotα,DB=10cot(45°-α),

所以AB=AD+DB

=10[cotα+cot(45°-α)]

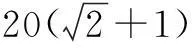
六、几何模型

例6A、B、C是我方三个炮兵阵地,A地在B地的正东,相距6千米,C地在B地的北偏西30°,相距4千米,P地为敌炮兵阵地,某时刻A地发现敌炮兵阵地的某种信号,由于B、C两地比A地距P地远,因此4秒后,B、C两地才同时发现这一信号(该信号的传播速度为每秒1千米),A炮位若炮击P地,求炮击的方位角.

分析由题意知,点P与点A、B的距离相距4千米,即|PB|-|PA|=4,依此可建立“双曲线”模型.

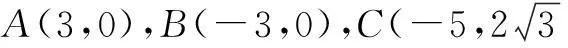
①

②