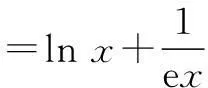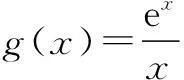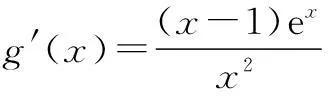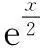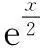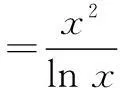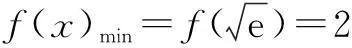构造双函数巧解一类不等式问题



构造双函数巧解一类不等式问题

魏正清

(甘肃省临泽第一中学，734200)

一、 不等式恒成立问题

(1)求f(x)的单调区间;

(2)当x∈(0,+∞)时,若不等式lnx+3ex3≤2x4+mx恒成立,求实数m的取值范围(e是自然对数的底数).

解(1)单调递增区间是(0,e),单调递减区间是(e,+∞)(过程略).

再令g(x)=3ex2-2x3(x>0).由g′(x)=6ex-6x2>0,得0

注这种方法可行的关键是所构造的函数f(x),g(x)满足(f(x)+g(x))max=f(x)max+g(x)max,否则将有(f(x)+g(x))max

二、 不等式有解问题

(1)求f(x)的单调区间及极值;

解(1)略.

∴f(x)min+g(x)min≤-1,

三、实数取值范围问题

例3已知函数f(x)=ax-lnx.

(1)是否存在正实数a,使f(x)的最小值是3?若存在求出a的值,若不存在,请说明理由;

(2)若存在实数x使x2-xlnx+ex-mx=0成立，求正数m的取值范围.

由(1)知f(x)=x-lnx在(1,+∞)内单调递增,在(0,1)内单调递减.

从而f(x)mim=f(1)=1,函数f(x)的值域为[1,+∞).

∴f(x)min+g(x)min≤m,即m≥e+1.

四、 不等式证明问题

(1)求f(x)的单调区间;

∴f(x)+g(x)>f(x)min+g(x)min

=2e-2e=0，