高一数学测试



○课外测试○

高一数学测试

一、填空题(本大题共14小题,每小题5分,共70分)

1.已知全集U={1,2,3,4,5},且A={2,3,4},B={1,2},则A∩(UB)等于______.

4.已知幂函数y=f(x)的图象经过点(-2,4),那么这个幂函数的解析式为______.

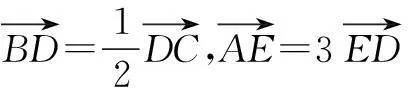
9.若关于x的方程2x2+(2-t)x+2=0的两个实根α,β满足0<α<1<β<2,则实数t的取值范围是______.

10.设单位向量e1、e2夹角是60°, a=2e1+e2,b=e1+te2,若a、b夹角为锐角,则实数t的取值范围是______.

11.设向量a、b、c满足a+b+c=0,(a-b)⊥c,|a|=1,则|b|=______.

13.已知函数f(x)=x5+x,对任意的m∈[-2,2],f(mx2+x)+f(x)<0恒成立,则x的取值范围为______.

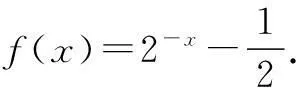
二、解答题(本大题共6题,共90分.解答应写出必要的文字说明、证明过程或演算步骤)

15. (本小题满分14分)已知

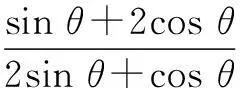
(2)求下式的值：

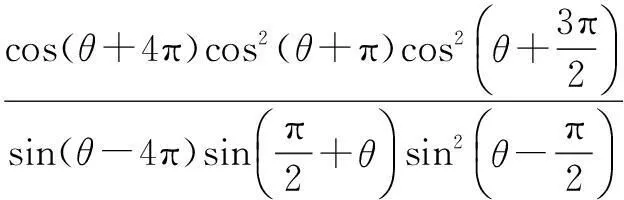
16.(本小题满分14分)平面内给定三个向量a=(3,2),b=(-1,2),c=(4,1).

(1)若(a+kc)⊥(2b-a),求实数k;

17.(本小题满分14分)在经济学中,函数f(x)的边际函数Mf(x)定义为Mf(x)=f(x+1)-f(x).某公司每月最多生产20台某种大型机械,生产x台(x∈N*)的收入函数为R(x)=30x-x2(单位:万元),其成本函数为C(x)=6x+40(单位:万元),利润是收入与成本之差.

(1)求利润函数P(x)及边际利润函数MP(x);

(2)利润函数P(x)与边际利润函数MP(x)是否具有相同的最大值?

(1)求函数f(x)的解析式及单调增区间;

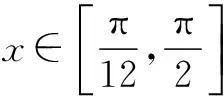
19.(本小题满分16分)已知函数

f(x)=ax2-8x-3.

(1)若对x∈R,f(x)≤x2-4x+1恒成立,求实数a的取值范围;

(2)对于给定的实数a,当x∈[0,M]时, |f(x)|≤5恒成立.

① 当a=6时，求M的最大值;

② 当a>0时，求M的最大值M(a).

20.(本小题满分16分)已知函数f(x)=log2x+2logx2,x∈(1,+∞).

(1)求函数f(x)的值域;

(2)设g(x)=(log2x+2a)2+4(logx2+a)2(x∈(1,+∞),a∈R),求g(x)的最小值φ(a).

参考答案

一、填空题

1. {3,4};2. 一; 3. 4π;

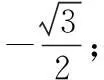
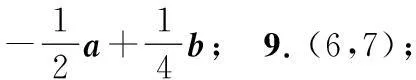
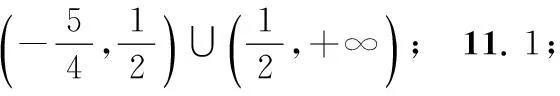
二、解答题

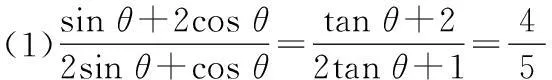
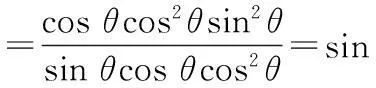
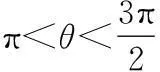
16.(1)由题意，知a+kc=(3+4k,2+k),

2b-a=(-5,2).

∵(a+kc)⊥(2b-a),

∴(3+4k)×(-5)+(2+k)×2=0,

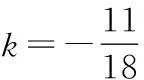
(2)设d=(x,y),由d∥c，得

x-4y=0.

①

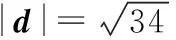
②

17.由题意，知x∈[1,20],且x∈N*.

(1)P(x)=R(x)-C(x)

=30x-x2-(6x+40)

=-x2+24x-40,

MP(x)=P(x+1)-P(x)

=-(x+1)2+24(x+1)

-40-[-x2+24x-40]

=23-2x.

(2)P(x)=-x2+24x-40

=-(x-12)2+104,

当x=12,(P(x))max=104(万元).

因为MP(x)=23-2x在[1,20]上是减函数,所以x=1时,(MP(x))max=21(万元).

因此,利润函数P(x)与边际利润函数MP(x)不具有相同的最大值.

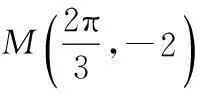
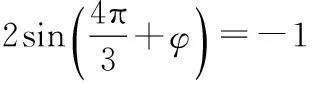
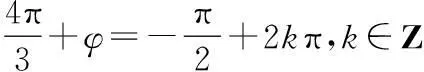
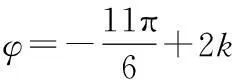
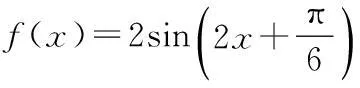
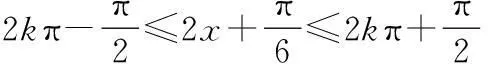
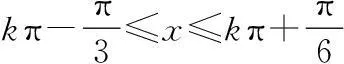
∴函数f(x)的单调增区间是

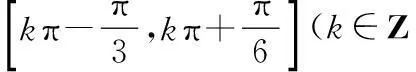
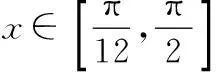
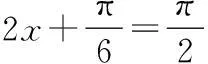
19.(1)对x∈R,ax2-8x-3≤x2-4x+1恒成立,即(a-1)x2-4x-4≤0对x∈R恒成立.

若a-1=0，即a=1时,不合题意,故a≠1.

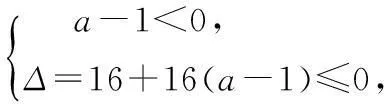
故实数a的取值范围是(-∞,0].

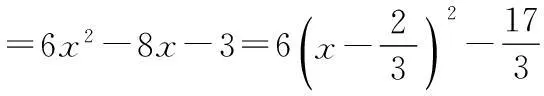
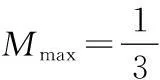
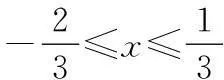
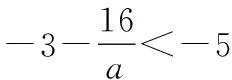
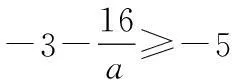
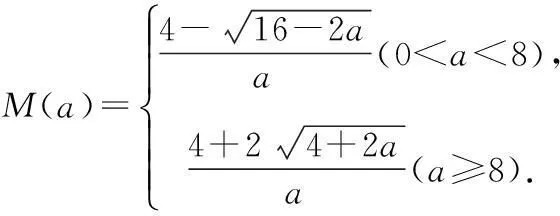
20.(1)∵f(x)=log2x+2logx2

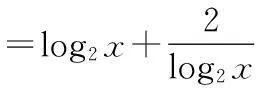
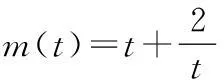
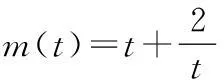
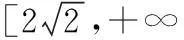
(2)∵g(x)=(log2x+2a)2+4(logx2+a)2

+8alogx2+4a2

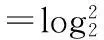
=(log2x+2logx2)2+4a(log2x+2logx2)

+8a2-4,

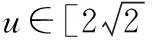
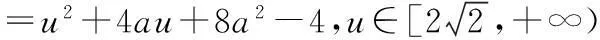
∵h(u)=u2+4au+8a2-4

=(u+2a)2+4a2-4，

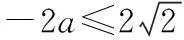
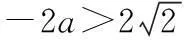
综上,