让数学课堂“动”起来——资兴市鲤鱼江完全小学数学组风采



让数学课堂“动”起来——资兴市鲤鱼江完全小学数学组风采

第一排左起：唐丽红　李懿娟　谷楚芳　喻朝阳　曹嫦艳　欧　慧　朱卫香　郭桂玉　黄小丽　廖菊英第二排左起：夏荣莲　陈彩兰　邵晓丽　赵文妮　黎林华　袁跃忠　蒋东锋　李　英　谢春艳　黄红燕　袁智琳第三排左起：陈满坤　代文君　张　红　袁光华　何　香　邓晓峰　欧名兰　陈美芳　曹晓燕　曹　英　许明玉第四排左起：李跃平　邝朝辉　郭剑云　黄仁辉　吴勇跃　黎忠辉　段高焱　曹　彪　李林峰　黄北平　黄　毅

资兴市鲤鱼江完全小学坐落在国家5A级景区——东江湖畔，有着70年历史。鲤鱼江完小的教师们如东江湖水一样，静静地孕育着一群群“小鱼”。新课改以来，学校数学组的教师们着重探索如何让数学课堂“动”起来。他们认为，在数学课堂教学中，重视学生在学习过程中积累基本活动经验，是让数学课堂“动”起来的关键。

经常开展“做”数学的活动。小学生在解决一些较抽象的数学问题时总感觉困难重重，很重要的一个原因是他们的数学活动经验十分匮乏。数学组教师针对这一现实情况，常常在课前布置学生准备一些学具，如小棒、纸片、包装盒、钟面等，在课堂教学中让学生自己动手摆一摆、说一说、想一想，在知识发生的过程中积累基本活动经验。虽说这些活动经验是零碎的，但却是学生在“做”数学的过程中亲自看到的、听到的、摸到的、想到的，是最真实的、最直接的、最有效的，能为顺利解决抽象的数学问题奠定良好的基础。

比如，曹彪老师教学完“周长”这一内容后，引入了练习题：用6个边长为1厘米的正方形拼成一个长方形，它的周长是多少？

这样抽象的题目，学生读懂题意都有些困难，更别说动手解题了。图片就是通往抽象的桥梁，曹老师不是急着让学生列式解答，而是让学生先用6个小正方形纸片在小组里摆一摆。在全班交流时，学生先是将3个小正方形纸片放在了上面，然后在下面放了3个小正方形纸片，拼成了一个长3厘米、宽2厘米的长方形（如图1）。还有学生将6个小正方形纸片排成一排，拼成了一个长6厘米、宽1厘米的长方形（如图2）。

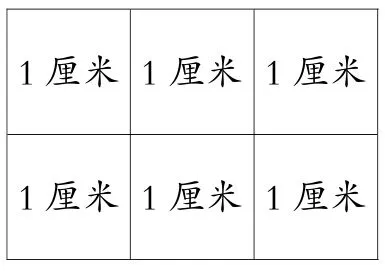
图1

图2

有了这样直观的图形，学生很快计算出了两个图形的周长，图1的周长是10厘米，图2的周长是14厘米。

在得到这些活动经验之后，一位爱动脑筋的小男孩皱起了眉头，不解地问道：“这两个图形的周长为什么会不一样呢？”曹老师神秘地说：“那你仔细想想，一定能找到答案的！”学生们开动脑筋，有的说是因为拼法不一样，图形的周长也不一样；有的说是因为小正方形露在外围的边数不一样，图形的周长就不一样……

学生似乎已经发现所拼长方形的周长都与小正方形的边长有关联，曹老师顺势让学生将6个小正方形的边长总和算了出来，是24厘米。将两次拼成的长方形的周长分别与24厘米进行比较，图1的周长比边长总和少了14厘米，图2的周长比边长总和少了10厘米。他让学生观察所拼图形，思考：“减少的边长都到哪去了？”学生仔细观察后，恍然大悟：原来这些边都躲在了图形里面，是不在周长计算范围之内的。图1的6个小正方形之间一共有7个接口，刚好减少了14条边，少了14厘米；图2的6个小正方形之间一共有5个接口，刚好减少了10条边，少了10厘米。一切仿佛都已水落石出。没有想到，有学生总结：小正方形之间每多1个接口，就会有2条边隐藏起来。随着这位学生的发现，其他学生也有了新的感悟：要使所拼的长方形的周长尽可能地小，就要让小正方形之间的接口尽可能地多。

在动手操作学具之后，学生为理性的认知积累了感性的经验，通过讨论与交流，能较好地理解：同样的6个小正方形拼成的长方形的周长不一定相等。

经常让学生合理地猜想。正如牛顿所说：“没有大胆的猜测，就做不出伟大的发现。”数学组教师也认为学数学首先要从猜想开始，一切源于思。教师们为了让学生孕育出数学猜想，给学生准备了大量的数学素材，引导学生进行观察、比较、分析、交流，在此基础上大胆地进行猜想，并为验证自己的猜想寻找证据。在教师们合理的引导下，学生们为了验证自己的猜想，主动地进行了一次又一次的探究，逐渐能有理有据地学数学。

谢春艳老师在教学五年级“平行四边形的面积”时，课始，在创设情境后利用课件呈现了3个面积相等的图形（如图3所示）。

图3

教材呈现的只有面积相等的两个图形（1和2），谢老师在此基础上增加了一个平行四边形（3），呈现了3个面积相等的图形。这样做的原因有两个。第一个是丰富学生的感性认识。学生在数格子的活动过程中就能发现3个图形的面积相等。如果两个图形的面积相等，可能是一种巧合，那么3个图形的面积分别相等，能更好地激发学生思考：它们三者之间有着什么内在的联系？或者说，它们之间有着什么共同点？这为学生进行第一次平行四边形面积计算公式的探究活动做好了准备，完成了“发现问题”与“提出问题”阶段。第二个是确保学生的研究方向正确。学生的认知水平、生活经验与数学素养各有差异，有时完全放手可能会让学生迷失前进的方向。根据“最近发展区”理论，这3个图形就成了从“现有认知区”通往“可能发展区”的台阶，让学生“跳一跳”能够够得着，保护他们学习的积极性。

接下来谢老师通过引导学生进行两次比较，鼓励学生大胆猜想。

第一次是同类图形的比较，即两个不同形状的平行四边形进行比较。通过观察，学生发现这两个平行四边形的底与高都分别相等，且两者的乘积恰好是12平方米，这一切难道是巧合吗？学生觉得意外，求知欲被激发。难道平行四边形的面积会是它的底与高的乘积吗？学生有了第一个猜想。

第二次是异类图形比较，即两个面积相等的平行四边形与长方形进行比较。通过观察，学生发现两个平行四边形的底和高与长方形的长和宽分别相等，且它们三者的面积也相等。这难道又是巧合吗？同样的巧合连续出现，再次激起学生的求知欲。难道平行四边形的底和高与长方形的长和宽存在着某种内在的联系吗？学生有了第二个猜想。

学生初步感知后有了两个猜想。紧接着，他们用剪拼的方法验证自己的猜想。在观察、比较中，学生发现：平行四边形的底就是所拼长方形的长，平行四边形的高就是所拼长方形的宽。因为长方形的面积= 长×宽，所以平行四边形的面积=底×高。学生在猜想、归纳推理中经历了知识发生的全过程，建构了正确的数学认知，发展了思维。

经常给学生“悟”数学的机会。数学组教师认为，在解决数学问题时，不仅应关注问题解决的结果，更应反思问题解决的过程。教师们为此经常在课堂教学中引导学生评价、反思自己解决问题的过程：如果是失败了，就查找原因；如果是成功了，就总结经验。学生在评价与反思中逐步学会了从事物的表面现象中发现其内在的规律，用心“悟”数学思想与方法。评价、反思的过程，实际上就是学生积累基本活动经验、对数学思想与方法再次领悟的过程。

李英老师在教学六年级的“数与形”时，设计了这样一个探究活动：用小正方形纸片摆一摆，试着用数形结合的思想说说2+4+6+8的计算规律。

学生以小组为单位完成了这一探究活动，完成情况如图4所示。

图4

教师将上述5种图形呈现出来，让学生自己先评一评，然后进行全班交流。学生发现①与②摆得有序，而且规律明显：每次都是在同一个位置上增加一个加数，每增加一个加数后，摆出的图形都是长方形，且长比宽多1。③用不同颜色的纸片代替不同的加数依次进行摆放，但摆放时没有按一定规律重复进行。④从左往右依次摆出了“2”“4”“6”“8”，最后为了摆出一个有规律的图形，采用了“移多补少”的方法完成了长方形的拼组。⑤中纸片的摆放随意性大，多数是拿到哪种颜色就摆哪种颜色，思维缺乏有序性。通过评价，学生悟出：每种颜色的纸片都代表着一个加数，摆放纸片要逐层进行。每摆完一个加数，就要看看形与数之间的联系，思考其中隐藏的规律。

在对各组所摆的图形进行评价、反思后，学生发现：2+4+6+8=（4）×（5）=20，“4”就是所摆长方形的宽，“5”就是所摆长方形的长，长比宽多“1”，长×宽=小正方形纸片的个数。学生利用这一发现，快速地完成了2+4+6+8+10=（）×（）=（）和2+4+6+8+10+12=（）×（）=（）的计算。在积累了大量的活动经验之后，学生还用语言概括出计算的规律：从2开始，n个连续偶数相加，它们的和就是n乘（n+1）的积。

经过这一探究，数学组的教师也有所悟：数形结合思想要靠教师引导学生对数与形的结合过程进行反思，通过联想、类比积累丰富的数形结合经验，逐步领悟数学思想。

课堂是教学的主阵地。鲤鱼江完小数学组的教师们就是这样组织学生在课堂上开展各种各样的数学活动，帮助学生获得基本活动经验，把数学味做足的。

（执笔：李英、黎林华、曹彪）

·校长寄语·