带指数参数的隐含波动率模型

吴小燕，王美清，庄 颖

(福州大学数学与计算机科学学院，福州350116)

带指数参数的隐含波动率模型

吴小燕，王美清，庄 颖

(福州大学数学与计算机科学学院，福州350116)

在广泛运用的Black-Scholes定价模型中，波动率被看作是一个固定的常数，但越来越多的实证分析表明这种假设在实际的期权市场中并不成立，隐含波动率具有“波动率微笑”和“期限结构”等特点。鉴于此，对Cassese和Guidolin提出的确定性隐含波动率模型进行改进，认为隐含波动率并不一定是关于在值程度的二次函数，采用指数参数项替代原模型中的在值程度二次项。最后基于AAPL股票期权进行实证分析，结果表明改进的模型更具灵活性，能更好地拟合和预测隐含波动率及期权价格。

Black-Scholes模型；隐含波动率曲面；参数模型；半参数模型；指数参数；非线性方程组

期权定价理论是金融工程领域研究的热点问题之一。1973年，美国数学家Black等[1]提出了第一个完整的期权定价模型，并推导出了著名的Black-Scholes期权定价公式(简称B-S公式)。该模型假设标的资产的波动率为常数，然而大量的研究分析表明，该假设在实际的金融市场是不成立的，隐含波动率具有“波动率微笑”和“期限结构”等特征[2-5]，即通过B-S公式反解出来的隐含波动率会因期权的执行价格和剩余期限的不同而不同。若把期权的隐含波动率、执行价格和剩余期限表示在三维坐标空间中，可得到一个非平坦的三维曲面，称之为“隐含波动率曲面”。这个曲面包含了期权市场上的大量信息，是期权定价和金融风险管理的重要工具，因此，对隐含波动率曲面的建模是金融工程领域的研究热点和难点。

对隐含波动率曲面的建模，目前已有的研究主要分为2类：确定性隐含波动率模型和随机隐含波动率模型。确定性隐含波动率模型认为隐含波动率的变化与剩余期限、执行价格或者在值程度(moneyness)之间存在确定性的函数关系，且这种关系不随时间发生变化。常见的确定性模型有3种：Derman[6]提出的粘性行权价规则(sticky strike rule)和粘性delta规则(sticky delta rule)及Daglish等[7]提出的平稳时间平方根规则(Stationary Square Root of Time Rule)。1999年Schonbucher[8]提出了随机隐含波动率模型的思想，认为隐含波动率的变化是由几个风险源驱动，并假设这些风险源与驱动标的资产价格变动的风险源不同。之后Ledoit等[9]、Cont等[10]、陈蓉等[11]沿用Schonbucher的思想，并在此基础上提出了新的模型。

近年来，对期权隐含波动率的研究主要集中在确定性隐含波动率模型的建立上[12-16]。1996年Ncube[17]采用FTSE100指数期权的市场数据，实证分析了期权隐含波动率、期权执行价格和剩余期限三者之间存在相关性。1998年Dumas等[18]基于这种相关性，采用S&P500指数期权的数据，说明三者之间存在一种线性关系，并提出一组隐含波动率曲面的参数模型。2006年Cassese等[19]沿用Dumas的思想，用在值程度替换原参数模型中的执行价格，并基于S&P500指数期权验证了新的模型具有更好的拟合效果。2009年Borovkova等[20]在Dumas的参数模型的基础上首次提出了半参数模型，认为当剩余期限固定时，隐含波动率是一个关于执行价格或在值程度的二次多项式函数，不同于参数模型中的参数对于不同剩余期限均是一定的情况，半参数模型中的参数随剩余期限变化。

Cassese等提出的参数模型使用在值程度的二次多项式来拟合隐含波动率，虽然二次多项式能够表现出隐含波动率微笑的特征，但其并不能很好地说明微笑的幅度，随着数据的变化，模型的拟合效果未必最好。因此，本文针对该问题提出改进，用指数参数项替代原模型中的二次项，并用AAPL股票(苹果公司股票)期权的市场数据对改进模型进行实证分析(文中所有市场数据均来自雅虎财经)。实证结果表明，改进的模型更具灵活性，能更好地拟合和预测隐含波动率及期权价格。

1 B-S模型及隐含波动率曲面

B-S模型在假设标的资产价格遵循几何布朗运动、无风险利率为常数、不支付红利、不支付交易费和税收、不存在套利、标的资产波动率为常数的前提下，给出期权价格、标的资产价格和时间之间的关系，可由下列偏微分方程刻画，

其中：V为期权价格；S为标的资产的价格；t为交易日期；r为年化无风险利率；σ为标的资产的波动率。在该模型中，除了波动率无法直接从市场上获得外，其余参数和变量均可由市场条件或合约给定。

从式(1)推导出的欧式看涨期权和看跌期权的定价公式分别如下：

其中：C为看涨期权的价格；P为看跌期权的价格；为标准正态分布的概率分布函数；K为期权的执行价格；T为期权的交割日期。已知(S,t,r,q,K,T,σ)，利用式(2)，(3)就可得到期权的价格。

B-S模型假定波动率σ是固定的常数，即在某一固定的时刻，计算同一标的资产的不同期权价格时，采用的波动率是相同的。若把某一时刻期权的隐含波动率、执行价格和剩余期限τ(τ=T-t)用三维坐标空间表示出来，会得到一个平坦的表面。然而大量实证研究表明，隐含波动率会随执行价格和剩余期限变化而改变。如，将AAPL股票期权在2016-03-01日时看涨期权的隐含波动率、执行价格和剩余期限之间的关系在三维坐标空间中表示，结果如图1。显然，隐含波动率并不是一个常数，而是与期权的执行价格K及剩余期限τ有关。

图1 2016-03-01日AAPL看涨期权的隐含波动率Fig.1 Implied volatilities ofAAPLstock option in 2016-03-01

如果能够确定隐含波动率、执行价格和剩余期限这三者之间的函数关系，那么，当已知期权的执行价格和剩余期限时，就可以预测期权的隐含波动率。

2 带指数参数的隐含波动率曲面模型

2.1 传统参数模型

Dumas对S&P500指数期权的隐含波动率σ，期权执行价格K及剩余期限τ等数据作了大量的实验分析，提出用执行价格和剩余期限的双二次多项式来拟合隐含波动率曲面，

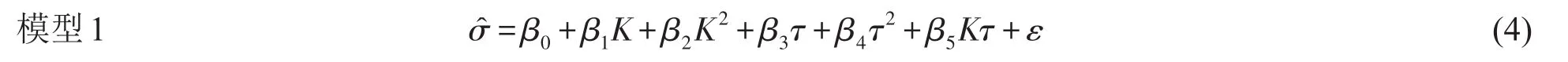
为了避免期权隐含波动率过分依赖于具体的执行价格和标的资产的价格走势，Cassese等考虑用期权的在值程度(moneyness)代替执行价格，这样，只需关注执行价格和资产价格之间的对比程度即可。期权的在值程度M反映了执行价格K与标的资产价格S之间的关系，定义如式(5)。

Cassese等用在值程度M替换模型1中的执行价格K，并且去掉剩余期限的二次项，给出了如下模型，即模型2

2.2 带指数参数模型

用模型2(式(6))对AAPL股票期权2016-03-01日的看涨期权的市场数据进行拟合，结果如图2所示。从结果看，模型2能够表现出“微笑”特征，但在M∈[-1,1]部分，曲面的弯曲太平缓，对实际数据的拟合效果不理想。

如果将式(6)中的在值程度M的二次项去除，模型修改为

其拟合的曲面如图3所示，并没有表现出隐含波动率“微笑”特征。

图2 式(6)拟合出的隐含波动率曲面Fig.2 Fitted implied volatility surface with formula(6)

图3 式(7)拟合出的隐含波动率曲面Fig.3 Fitted implied volatility surface with formula(7)

显然，模型2对隐含波动率的“微笑”的近似主要依赖于在值程度M的二次项，但并不能得到理想效果。若用Mα(0＜α＜2)代替M2，但是当M＜0且α为非整数时，Mα可能是虚数。另外，M的绝对值项 |M|能够呈现一定的弯曲趋势，因此本文考虑用来代替模型2中的M2项，其中α＞0。基于以上分析，本文提出改进模型，将模型2修正为如下带指数参数模型，

利用最小二乘法对历史数据进行拟合，可以求解模型3中的各个未知参数。在某一时刻，假定标的资产的价格为S，无风险利率为r。在S上立了n支期权，第i支期权的价格为Vi、隐含波动率为σi及其对应的执行价格和剩余期限为(Ki,τi)，相应的在值程度为Mi。因此有n组数据(τi,Mi,σi)，i=1,…,n。利用最小二乘求模型3的参数问题，转化为以下极值问题，

由极小值原理可知，极值问题的解等价于下列非线性方程组的解：

为方便起见，将模型3中的参数用向量表示为X=(β0,β1,β2,α,β3,β4)T，将方程组(10)记为函数向量F(X)，显然F(X)关于X连续可微，其对应的Jacobi矩阵为

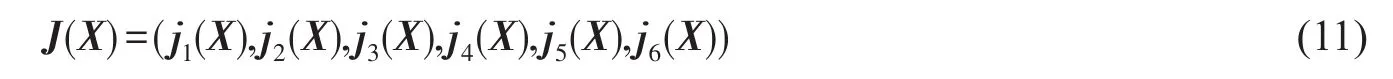
其中ji(X),i=1,…,6，表示矩阵J(X)的第i个列向量：

2.3 模型3的数值求解

求解非线性方程组最常用的是Newton迭代法，该方法要求方程组的Jacobi矩阵可逆。但是方程组(10)对应的Jacobi矩阵中的元素是随着实际市场数据的变化而变化，因此不能保证J(X)非奇异，为解决此问题，本文采用修正的Levenberg-Marquardt算法[21-22]，该方法不要求J(X)可逆，且具有全局收敛性。

定义第k步迭代的步长为

第k步迭代的实际下降量和预估下降量分别为二者的比值记为

rk用来决定是否接受试探步长dk以及如何调整迭代参数μk的大小。rk越大，说明函数下降越多，此时接受dk并希望步长增大，因此减小μk；rk越小，说明函数下降越少，此时拒绝dk并希望步长减小，因此增大μk。算法步骤如下：

步骤1：给定定义域内的初始值X0，ε≥0,μ1＞m＞0,0≤p1≤p2＜1,k∶=0；

步骤3：计算rk，并设置

步骤4：调整参数μk，

k∶=k+1，转步骤2。

依照上述步骤即可求得非线性方程组(10)的最优解X*，同时X*也是模型3的最优拟合参数。

2.4 基于模型3的半参数模型

2009年Borovkova等[20]在Dumas的参数模型的基础上拓展了半参数模型，此类模型认为当剩余期限固定时，隐含波动率是一个关于执行价格(或在值程度)的二次函数，不同于参数模型中的参数对于不同剩余期限都是一定的情况，半参数模型中的参数是随剩余期限变化的。参数模型2和本文改进的模型3对应的半参数模型分别如下：

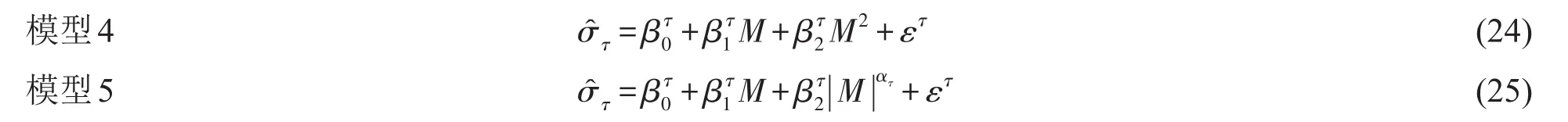
在某一交易日，对任意固定的剩余期限，都需对上述半参数模型进行最小二乘拟合，进而得到M方向上的函数，为了得到隐含波动率曲面，本文在τ方向上采用双三次样条方法进行插值。半参数模型拟合的隐含波动率曲面的形状较参数模型更加丰富，更贴近实际应用。

3 模型验证

验证中模型的求解用MATLAB软件编程实现。

3.1 实验数据的选取

从市场上获取AAPL股票及其期权的相关数据(S,t,r,K,T,σ,C)。选取2016-03-01日到2016-03-31日的市场交易数据，并进行如下筛选：

1)选择剩余期限处于6天到1年之间的数据；

2)为了能真实地反映实际情况，删除交易量小于20的数据。

3.2 实验结果与分析

通过修正的L-M算法分别用模型2、模型3、模型4和模型5拟合选择的市场数据，得到关于K和τ的隐含波动率函数，并通过此函数求出(Ki,τi)对应的隐含波动率的估计值̂i，同时由式(2)求出对应的期权价格的估计值分别采用以下测量误差的指标来观察模型对期权市场数据的拟合和预测效果：

5)某个交易日内，期权价格的估计值介于市场买卖价之间的比例为

其中：n为该交易日内期权的总量；m表示期权价格的估计值介于市场买卖价之间的期权总量。

首先用带指数参数的隐含波动模型3对2016-03-01日到2016-03-31日的市场数据进行最小二乘拟合，并对拟合所得的指数参数项的系数β2及其指数参数α进行分析。参数β2和α的拟合结果如表1。

表1 模型3中参数β2及α的拟合结果Tab.1 Fitted results ofβ2andαin model 3

观察表1可知，由模型3拟合市场数据而得的指数项|Mα|的系数β2均非零，且其指数参数α也并非固定的常数，而是随市场数据的变化而改变的，这说明模型3中的指数项在对市场数据进行拟合时起到了一定作用，同时可以通过调整参数α改变模型的拟合效果。

为了进一步分析模型3较模型2在数据拟合及预测的效果上的差异，本文分别用参数模型2及模型3对2016-03-01至2016-03-31日的市场数据进行拟合，并用第t天拟合的隐含波动率函数去预测第t+1天的隐含波动率和期权价格，分别对其拟合、预测误差求均值及方差，结果见表2。

表2 参数模型2和模型3的拟合及预测结果Tab.2 Fitted and predicted results of the parametric model 2 and model 3

为了分析半参数模型4和模型5的拟合及预测效果，下面分别用模型4和模型5对2016-03-01日的市场数据进行拟合，并用拟合得到的半参数模型对2016-03-02日的对应交割日期的隐含波动率进行预测，分别对其拟合、预测误差求均值及方差，结果见表3。

表3 半参数模型4和模型5的拟合及预测结果Tab.3 Fitted and predicted results of the semi-parametric model 4 and model 5

观察表2，3可知，改进的带指数参数模型3及其对应的半参数模型5的估计误差均小于模型2和模型4的估计误差，且改进模型估计的期权价格介于市场上买卖价之间的比例也较原模型高，验证了本文改进的带指数参数模型较二次多项式模型更加灵活，更加适用多变的金融市场。

4 结 论

基于Cassese等提出的拟合期权隐含波动率曲面的参数模型，本文进行了改进，用指数参数项 ||Mα代替了原模型中的二次项M2项，使得改进模型中的在值程度的次数不再是固定的二次，而是根据实际的期权数据拟合所得，使得模型更具灵活性，即可以根据不同的期权数据来调整α的取值，从而较好地拟合和预测期权的隐含波动率及其价格，更加贴近实际应用。

[1]BLACK F,SCHOLES M.The pricing of options and corporate liabilities[J].The journal of political economy,1973,81(3):637-654.

[2]DUAN J C.Conditionally fat-tailed distributions and the volatility smile in options[R].Rotman School of Management,University of Toronto,Working Paper,1999.

[3]HEYNEN R,KEMNAA,VORST T.Analysis of the term structure of implied volatilities[J].Journal of Financial and Quantitative Analysis,1994,29(1):31-56.

[4]MUZZIOLI S,RUGGIERI A.A comparison of fuzzy regression methods for the estimation of the implied volatility smile function[J].Fuzzy Sets and Systems,2015,266:131-143.

[5]HAN Q,LIANG J,Wu B.Cross economic determinants of implied volatility smile dynamics:three major European currency options[J].European Financial Management,2015,doi:10.111/EUFM.12072.

[6]DERMAN E.Regimes of volatility[J].Risk,1999,4:55-59.

[7]DAGLISH T,HULL J,SUO W.Volatility surfaces:theory,rules of thumb,and empirical evidence[J].Quantitative Finance,2007, 7(5):507-524.

[8]SCHONBUCHER P J.A market model for stochastic implied volatility[J].Philosophical Transactions of the Royal Society of LondonA:Mathematical,Physical and Engineering Sciences,1999,357(1758):2071-2092.

[9]LEDOIT O,SANTA-CLARA P.Relative pricing of options with stochastic volatility[R].University of California-Los Angeles Finance Working Paper,1998:9-98.

[10]CONT R,DAFONSECAJ.Dynamics of implied volatility surfaces[J].Quantitative finance,2002,2(1):45-60.

[11]陈蓉,吕恺.隐含波动率曲面:建模与实证[J].金融研究，2010(8):136-154.

[12]KAMAL M,GATHERAL J.Implied volatility surface[M]//CONT R.Encyclopedia of Quantitative Finance.[S.L.]:Witey,2010.

[13]HOMESCU C.Implied volatility surface:Construction methodologies and characteristics[J].SSRN Electronic Journal,2011,doi:10.2139/ssrn.1882567.

[14]FENGLER M R.Option data and modeling BSM implied volatility[M]//Handbook of Computational Finance.Berlin:Springer, 2012:117-142.

[15]ZHAO B,HODGES S D.Parametric modeling of implied smile functions:a generalized SVI model[J].Review of DerivativesResearch,2013,16(1):53-77.

[16]FENGLER M R,HIN L Y.Semi-nonparametric estimation of the call-option price surface under strike and time-to-expiry noarbitrage constraints[J].Journal of Econometrics,2015,184(2):242-261.

[17]NCUBEM.ModellingimpliedvolatilitywithOLSandpaneldatamodels[J].JournalofBankingandFinance,1996,20:71-84.

[18]DUMAS B,FLEMING J,WHALEY R.Implied volatility functions:empirical tests[J].Journal of Finance,1998,53:2059-2106.

[19]CASSESE G,GUIDOLIN M.Modelling the implied volatility surface:does market efficiency matter?:An application to MIB30 index options[J].International review of financial analysis,2006,15(2):145-178.

[20]BOROVKOVA S,PERMANA F J.Implied volatility in oil markets[J].Computational Statistics&Data Analysis,2009,53(6): 2022-2039.

[21]YAMASHITA N,FUKUSHIMA M.On the rate of convergence of the Levenberg-Marquardt method[M]//Topics in Numerical Analysis.Vienna:Springer,2001:239-249.

[22]FAN J Y.A modified Levenberg-Marquardt method for singular system of nonlinear equations[J].Journal of Computational Mathematics,2003,21(5):625-636.

责任编辑：丁吉海

Implied Volatility Model with Index Parameter

WU Xiaoyan,WANG Meiqing,ZHUANG Ying
(College of Mathematics and Computer Science,Fuzhou University,Fuzhou 350116,China)

In the widely used Black-Scholes pricing model,the volatility is assumed to be a fixed constant. However,more and more empirical analyses have proved this assumption is incorrect in the real option market, the implied volatility has two key features:volatility smile and term structure.This paper modifies the deterministic implied volatility model proposed by Cassese and Guidolin,it deems implied volatility is not necessarily the quadratic function of moneyness and replaces the quadratic term of moneyness with an index parameter term. With the modified model some empirical analyses based on AAPL stock option are carried out.The experimental results show that the modified model is more flexible and has a better fitting and forecasting ability.

Black-Scholes model;implied volatility surface;parametric models;semi-parametric models;index parameter;nonlinear system of equations

F 830.91

A

10.3969/j.issn.1671-7872.2016.04.016

1671-7872(2016)04-0396-08

2016-07-22

福建省自然科学基金项目(2015J01013)

吴小燕(1989-)，女，河南平顶山人，硕士生，研究方向为计算金融。

王美清(1966-)，女，福建福州人，教授，博导，主要研究方向为数值计算基础，计算金融。