六自由度机器人的运动学分析

王梦涛，张良安

(安徽工业大学机械工程学院，安徽马鞍山243032)

六自由度机器人的运动学分析

王梦涛，张良安

(安徽工业大学机械工程学院，安徽马鞍山243032)

针对一种自主研发的二三四轴相互平行的六自由度机器人，通过D-H(Denavit-Hartenberg)法建立机器人连杆坐标系和变换矩阵，求得正运动学方程，基于矩阵逆乘的思路进行逆运动学的求解，提出此类六自由度机器人逆运动学求解的方法，求出逆运动学的全部解析解。针对该机器人的奇异性，提出奇异位置逆解的处理方法，并用MATLAB机器人工具箱Robotics Toolbox验证了正解模型和逆解算法的正确性。研究结果为该机器人后续的轨迹规划和控制提供理论依据，对于具有相似结构的机器人运动学正逆解问题具有借鉴意义。

六自由度机器人；运动学；机器人工具箱；奇异性

在2015上海、苏州的工业机器人展览会上，众多机器人厂商纷纷推出其3～10 kg轻载机器人产品，如日本那智不二越的MZ系列六自由度机器人、德国KUKA的LBR iiwa机器人、瑞士ABB的YuMi机器人等。一种新的被称为“协作机器人”的轻载机器人正越来越多地出现在人机协作的场合，有望填补全手动装配与全自动生产线之间的差距[1]，由此看出轻载机器人有较好的应用前景。

机器人的正运动学和逆运动学是机器人研究中的关键问题，其中逆解的研究广受关注。求正解中常采用D-H(Denavit-Hartenberg)法得到连杆变换矩阵，将连杆变换矩阵相乘得到正解方程[2]。求逆解常见的方法有解析解法和数值解法，其中解析解法进一步划分为几何解法与代数解法[3]，而数值解法由于需要迭代，一般比解析解法慢。Paul等[4]提出的反变换解析法对于多自由度机器人求逆解十分有效；Pieper等[5]针对末端三轴交于一点的机器人提出Pieper法；王英石[6]采用旋量理论求解冗余机器人的运动学问题；姜宏超等[7]针对自主研发的六自由度模块化机器人，采用矩阵逆乘求出了16组逆解；邱宁佳等[8]针对六自由度机器人空间划线的具体应用，限定关节角度，并由运动时关节约束简化求逆解过程，避免了使用矩阵求逆解或高斯消去法等相对繁琐的算法；曾剑等[9]针对六自由度喷涂机器人，采用臂、腕分离法(即Pieper法)求出该机器人正逆运动学的解析表达式；耿磊[10]采用局部消元法求得库卡六自由度工业机器人逆运动学的解析解。

以上逆解算法多针对末端三轴相交的机器人，该机器人与二三四轴相互平行的六自由度机器人结构不同。基于D-H法求解二三四轴相互平行与末端三轴相交的机器人的运动学问题，其求解方法不能通用，而目前较少学者研究二三四轴相互平行机器人的运动学问题。为此，笔者针对二三四轴相互平行的六自由度机器人，采用D-H法求解机器人的运动学正逆解问题，且对其奇异性进行分析，使用Robotics Toolbox工具箱验证所求正逆解模型的正确性。

1 运动学模型的建立

1.1 机器人结构设计

六自由度机器人存在封闭解有两个充分条件[11]：3个相邻关节交于一点；3个相邻关节轴相互平行。多数焊接机器人满足第一个条件，而丹麦优傲机器人UR系列和北京遨博智能的OUR系列机器人则满足第二个条件。本文研究的六自由度机器人为自主研发的机器人，满足第二个条件，其三维模型如图1。图中数字1，…，6表示关节轴线，由图1可以看出，该机器人二三四轴相互平行。

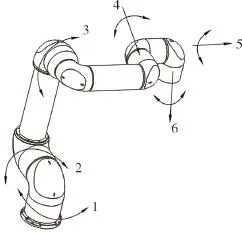
图1 六自由度机器人整体结构及转动关节Fig.1 Structure and rotation joints of 6 degree-of-freedom robot

1.2 连杆坐标系的建立

采用D-H法[12]建立连杆坐标系，在每个连杆上固接一个坐标系，通过坐标系之间的齐次变换矩阵相乘，可得到机器人末端相对于基坐标系的位姿矩阵。针对二三四轴相互平行的六自由度机器人，其连杆坐标系Ok-XkYkZk的建立过程为：坐标轴Zk为图1所示关节轴线j(j=1,…,6)，方向任意；找出相邻两轴线j和j+1的公垂线，坐标轴Xk与公垂线重合，方向指向轴j+1，关节公垂线与轴j的交点为坐标系Ok-XkYkZk的原点；若轴j与j+1相交，则取交点为坐标系Ok-XkYkZk的原点，坐标轴Xk为Zk与Zk+1的法线，方向任意；若轴j与轴j+1平行，原点取在使Xk到Xk+1沿Zk+1方向距离为零的位置，坐标轴Xk为相邻两关节轴线j和j+1的公垂线，方向指向轴j+1；基坐标系O0-X0Y0Z0与基座固接，可任意规定，一般使坐标轴Z0与Z1重合；末端连杆坐标系O6-X6Y6Z6原点可任意选取，坐标轴X6选取方法为当关节变量为零时，X6与X5重合；坐标系的Y轴按右手法则确定。

建立的二三四轴相互平行的六轴机器人连杆坐标系如图2。其中基坐标系原点O0与第一连杆坐标系原点O1重合，第五连杆坐标系原点O5与第六连杆坐标系原点O6重合。表1为六自由度机器人连杆参数。

表中：ai-1表示连杆长度(i=1,…,6)，即从Zk-1到Zk沿坐标轴Xk-1方向的距离；αi-1表示连杆扭角，即从Zk-1到Zk绕坐标轴Xk-1旋转的角度；di表示从Xk-1到Xk沿坐标轴Zk方向的距离；θi表示从Xk-1到Xk绕坐标轴Zk旋转的角度；a2=582 mm;a3=424 mm；d2=240 mm；d5=329 mm。

2 运动学分析

机器人的运动学包括正运动学问题和逆运动学问题，由关节角度确定末端位姿是正运动学问题，也称运动学正解。由末端位姿确定各关节的角度是逆运动学问题，也称运动学逆解。正解是逆解的基础，可用来验证逆解的正确性。在工业应用时，常常给定一系列末端位置，通过逆解求得每个位置对应的关节角度，控制电机转动使每个关节到达求得的位置，从而使末端到达给定的位姿。

2.1 正运动学求解

连杆i相对于连杆i-1的变换矩阵为

式(1)由4个参数ai-1、αi-1、di、θi决定，只有变量θi不确定，即变换矩阵随θi变化而变化。文中六自由度机器人连杆坐标系O6-X6Y6Z6相对于基坐标系O0-X0Y0Z0，其变换矩阵为各变换矩阵相乘，为

式中：nx，ny，nz分别表示坐标系O6-X6Y6Z6的坐标轴X6相对于基坐标系O0-X0Y0Z0在X，Y，Z轴的方向余弦；ox，oy，oz分别表示坐标系O6-X6Y6Z6的坐标轴Y6相对于基坐标系O0-X0Y0Z0在X，Y，Z轴的方向余弦；ax，ay，az分别表示坐标系O6-X6Y6Z6的坐标轴Z6相对于基坐标系O0-X0Y0Z0在X，Y，Z轴的方向余弦；px，py，pz表示坐标系O6-X6Y6Z6相对于基坐标系O0-X0Y0Z0的位置坐标。

2.2 逆运动学求解

六自由度机器人的逆运动学求解是给定末端位置和姿态，求出各关节变量，其解可能存在多重解，也可能无解。文中基于矩阵逆乘的方法，即Paul等[4]提出的反变换方法，对机器人关节变量进行求解。

二三四轴相互平行的六自由度机器人，不同于常见的三轴相交于一点的六自由度机器人，采用矩阵逆乘的方法求逆解时每个关节角求解的顺序很重要。求平行关节角度时，需先求平行关节的关节角度和，再用和减去单个关节角度得到其余关节角度，即求逆解的过程中先求θ1,θ5,θ6，后求θ2,θ3,θ4。求θ2,θ3,θ4时，先求θ2,θ3,θ4这3个平行关节的一个角度θ2，然后求θ23，通过(θ23-θ2)求得θ3，再求θ234，用(θ234-θ23)求解θ4。其中θ23=θ2+θ3，θ234=θ2+θ3+θ4。

2.2.1 求解θ1,θ5,θ6

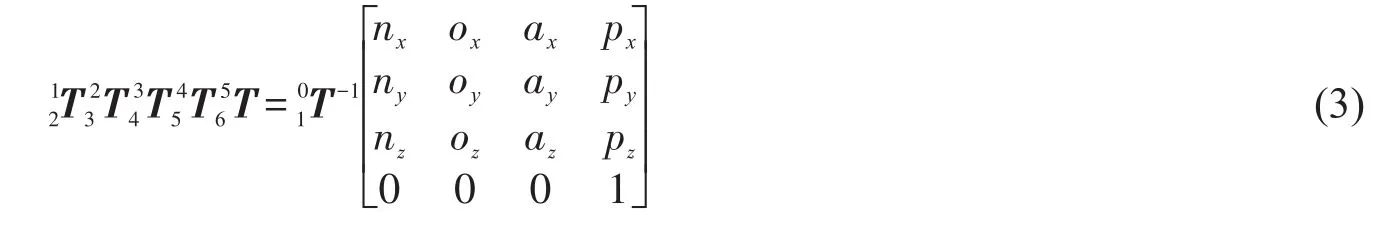
令式(3)两边矩阵第二行第四、三、二、一列元素相等，可得下面4个方程：

其中s1=sinθ1,c1=cosθ1，其余类推。由式(4)得

由式(5)得

进而得到θ5的解，因为θ1有2个解，所以对应θ5有4个解。

由式(6)，(7)得θ6与θ5一一对应，有4个解。

2.2.2 求解θ2,θ3,θ4

已求出θ1，θ5，θ6，将式(2)改写成

由式(11)两边第一、三行第四列的元素相等，得

式中：c23=cosθ23=cos(θ2+θ3)；s23=sinθ23=sin(θ2+θ3)；m1,m2分别为式(11)右边第一行第四列和第三行第四列的元素，m1,m2对应θ1、θ5、θ6各有4个值。

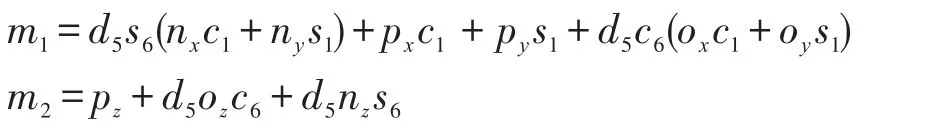
将式(12)含θ23项移到一边，得

式(13)两边取平方后相加，得

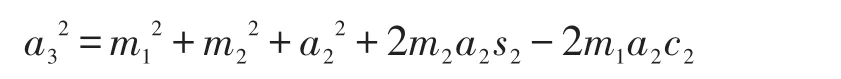
则可解得θ2的两组解，因为m1,m2有4个值，所以θ2有8个解，即

求出θ2，则由式(13)得

求得θ23，减去θ2可得θ3，θ3有8个解，且与θ2一一对应。

由式(11)两边第三行第一列、第三行第二列元素相等，得

则可求得

由式(15)，(18)求得

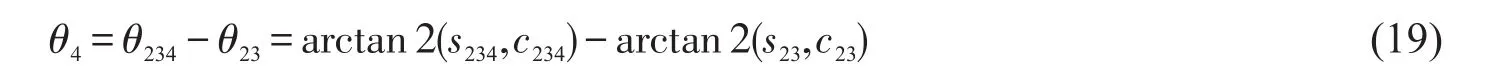
θ234有4个值，且与θ23的8个值对应，故θ4有8个解。

2.3 奇异性分析

机器人在奇异位置时运动学逆解会发生跳变，这对后期的轨迹规划造成潜在危险。如果机器人的逆运动学具有解析形式的解，根据文献[5]，可通过判断该解的代数式分母为零等异常情况，找到机器人的可能奇异点。在这些可能奇异点位置，如果机器人雅可比矩阵行列式的值为零，则机器人处于奇异位置。

针对二三四轴相互平行的六自由度机器人，逆运动学存在解析形式的解，即式(10)。当s5=sinθ5=0时，式(10)出现分母为零的情况，通过计算可得机器人的雅可比矩阵行列式的值为零，所以sinθ5=0时机器人处于奇异位置。此时θ6可取任意值均满足给定的约束，对此需对奇异点附近的θ6作平滑处理，避免θ6发生跳变，同时保证机器人的运动精度。

3 运动学正逆解的仿真验证

比较采用机器人工具箱Robotics Toolbox[13]与正解模型式(2)求得的正解，若两者相差小于10-4，则式(2)得到验证。将求得的8个逆解代入Robotics Toolbox求得位姿矩阵与最初给定的位姿矩阵且进行比较，若两矩阵前三行三列相差小于10-4，第四列相差小于10-2，则逆解得到验证。

3.1 运动学正解的验证

采用机器人工具箱Robotics Toolbox中提供的函数对六自由度机器人建模，并进行正运动学仿真。主要MATLAB代码为：

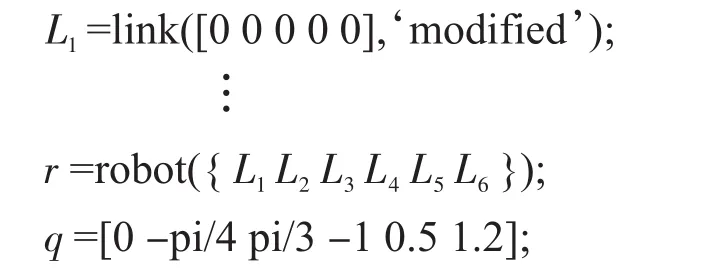
L1，…，L6表示工具箱Robotics Toolbox中link函数，‘link’是Robotics Toolbox中的函数，用来创建杆件坐标系，调用方法为

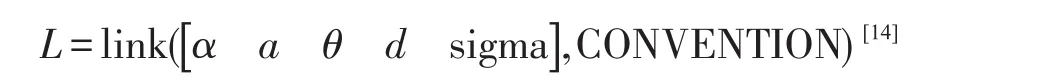
其中：参数α,a,θ,d为表1中的连杆参数。‘sigma’表示关节类型，0表示旋转关节，非0表示平动关节，这里取0；CONVENTION可以取‘standard’或‘modified’，‘standard’表示采用标准D-H法得到的连杆参数[15]，‘modified’表示采用改进的D-H法得到的连杆参数[16]，这里取‘standard’；q表示6个关节的变量θi；函数‘fkine’用来求正解。采用相同的关节变量θi由式(2)求正解。通过机器人工具箱与正解模型式(2)求得的正解均为

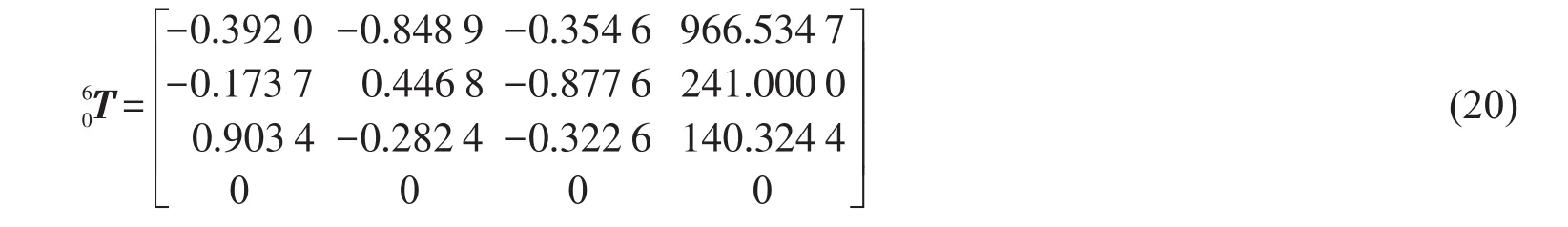
2次求得的结果保留小数点后4位相等，随机取多个不同的q同样满足正解结果相等，证明运动学正解模型正确。

3.2 运动学逆解的验证

设定目标位姿矩阵为式(20)，采用2.2节的求逆解过程编写程序求得8个逆解，表2中序号1～8为所求的逆解。使用Robotics Toolbox工具箱的‘fkine’函数求逆解对应的位姿矩阵，如B1,…,B8。

表2 8个逆解Tab.2 Eight solutions of inverse kinematics

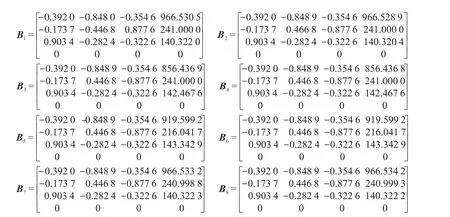
从表2可以看到，逆解3与4相同，逆解5与6相同，实际只有6组逆解。比较B1～B8可以看出，B1、B2、B7、B8与式(20)前三行三列相同，相差小于10-4，第四列（位置坐标）相差小于10-2，偏差在工程应用允许范围内；B3、B4、B5、B6与式(20)相差较大，认为逆解3、4、5、6是错误解，逆解1、2、7、8是正确解。只求出4组正确逆解并不代表逆解模型错误，而是表明此时机器人只有4组逆解。通过计算发现大部分位姿时机器人有8组逆解，而有些位姿时机器人逆解少于8组，所以在计算逆解时需代回正解模型中验证，剔除多余的逆解。

4 结 论

针对自主设计的一种二三四轴相互平行的六自由度机器人，对其进行运动学分析，得出以下结论：

1)运用D-H法求得该机器人运动学正解，基于矩阵逆乘的思路求得运动学逆解，进行逆运动学求解时，关节角的求解顺序很关键，求平行关节角度时，需先求平行关节的角度和，再相减得到其余关节角度；

2)当六自由度机器人处于奇异位置即sinθ5=0时，求逆解时，θ6取任意值均满足给定的约束；

3)运用机器人工具箱Robotics Toolbox对正逆解进行验证，结果表明所求正逆解是正确的，由此进一步表明该正逆解模型可以用于此类机器人后续轨迹规划和控制。

[1]艾斯本·奥斯特加.你的新同事：走出牢笼的机器人[J].办公自动化，2014(15):25-27.

[2]余晓流，刘进福，汪丽芳.基于ADAMS的六自由度焊接机器人运动学分析及仿真[J].安徽工业大学学报(自然科学版)，2012,29(1):49-51.

[3]CRAIG J J.机器人学导论[M].贠超，译.北京：机械工业出版社，2004:83-88.

[4]PAUL R P,SHIMAO B E,MAYER G.Kinematics control equations for simple manipulators[J].IEEE Transactions on Systems, Man and Cybernetics,1981,11(6):449-445.

[5]PIEPER D,ROTH B.The kinematics of manipulators under computer control[C]//Proc of the 2ND International Congress on Theory of Machines and Mechanisms.Zakopane:Springer,1969:159-169.

[6]王英石.冗余机器人的运动学及轨迹规划的研究[D].天津：南开大学，2014:35-40.

[7]姜宏超，刘士荣，张波涛.六自由度模块化机器人的逆运动学分析[J].浙江大学学报(工学版)，2010,44(7):1348-1354.

[8]邱宁佳，隋振，李明哲，等.六自由度机器人空间划线轨迹规划算法[J].吉林大学学报(工学版)，2013,43(5):1307-1313.

[9]曾剑，林义忠，廖小平，等.6R型喷涂机器人运动学分析及仿真[J].机械设计与制造，2010(6):145-147.

[10]耿磊.六自由度工业机器人的建模与仿真研究[D].沈阳：东北大学，2013:20-23.

[11]熊有伦，丁汉，流恩沧.机器人学[M].北京：机械工业出版社，1993:74-75.

[12]DENAVIT J,HARTENBERG R S.A kinematic notation for lower pair mechanisms based on matrices[J].ASME Journal of Applied Mechanics,1955,77(6):215-221.

[13]CORKE P.Arobotics toolbox for MATLAB[J].IEEE Robotics andAutomation Magazine,1996,3(1):24-32.

[14]谢斌，蔡自兴.基于MATLAB Robotics Toolbox的机器人学仿真实验教学[J].计算机教育，2010(19):140-143.

[15]PAUL R P.Robot Manipulators:Mathematics,Programming and Control[M].Cambridge,Massachusetts:MIT Press,1981: 98-100.

[16]CRAIG J J.Introduction to Robotics:Mechanics and Control[M].3rd ed.New York:Prentice Hall,2005:21-30.

责任编辑：何莉

KinematicsAnalysis of 6 Degree-of-freedom Robot

WANG Mentao，ZHANG Liang''an
(School of Mechanical Engineering,Anhui University of Technology,Ma'anshan 243032,China)

For a developed 6 degree-of-freedom robot with 2,3 and 4-axis parallelled to each other,a forward kinematics equation of the robot was acquired by establishing the link coordinate system and transformation matrix with D-H(Denavit-Hartenberg)method.Based on the idea of matrix inversion,the inverse kinematics calculation method of 6 degree-of-freedom robot was proposed,and all analytical solutions of the inverse kinematics were obtained.According to the singularity of the robot,the processing method of the inverse solution of the singular position was proposed,the forward kinematics model and inverse kinematics solution were verified by Robotics Toolbox in MATLAB software.The research results provide a basis for later trajectory planning and control of the robot,and it is a reference for the kinematics of the robot with similar structure.

6 degree-of-freedom robot；kinematics；robotics toolbox；singularity

TP 242.2

：A

10.3969/j.issn.1671-7872.2016.04.011

1671-7872(2016)04-0365-07

2015-07-14

国家自然科学基金项目(51375014)

王梦涛(1992-)，男，安徽灵璧人，硕士生，研究方向为机器人机构学及工业机器人控制技术。

张良安(1981-)，男，浙江杭州人，博士，副教授，主要研究方向为自动化生产线和机器人机构学。