基于实时跟踪的ARIMA大坝安全监控模型

黄梦婧，杨海浪，叶根苗(.河海大学水利水电学院，南京 20098；2.河海大学水文水资源与水利工程科学国家重点实验室，南京 20098；.安徽省引江济淮工程有限责任公司，合肥 2000)

大坝在正常运行时能起到巨大的效益，但是一旦溃坝会给下游造成巨大的损失，因此，确保大坝安全运行非常重要，应加强大坝安全监测的力度。为了更准确地了解大坝的运行状态，一个重要的方法是建立大坝安全监测模型，并通过分析变形规律，对大坝的安全性进行评价。能否有效地进行大坝变形监测，对保证大坝的正常运行，保障下游人民的生命财产安全具有重要的意义[1,2]。由于在大坝运行的过程中，大坝的变形过程较为复杂，会受到水压力、泥沙压力、扬压力、温度荷载等各种因素的影响，因此，如何建立一种最为优化并具有普遍性的分析模型仍有待研究。

由于在实际工程中，大坝变形实测值的时间序列一般是不平稳的，会有一定的趋势变化。基于此，我们提出建立差分自回归移动平均模型(ARIMA)来对此类不平稳的时间序列的变化过程进行分析。为了提高ARIMA模型的精度以及预测长度，使用了实时跟踪算法对原ARIMA模型进行优化，即提出基于实时跟踪的ARIMA模型，并将其应用于大坝安全监控及预报中。

1 ARIMA模型

1.1 ARIMA模型定义

差分自回归移动平均模型，这是一种时间序列建模的方法，基于对时间序列特征的分析，并由3个参数来建立模型，参数分别为自回归阶数p，差分次数d和移动平均阶数q[3]，模型表示为ARIMA(p,d,q)。

对于非平稳的时间序列{ct,t=0,±1,…}差分d次后获得一个平稳的时间序列{xi}，满足式(1)，模型建立为ARIMA(p,d,q)。

xt=∑pm=1φmzt-m-∑qj-1θjat-j+at

(1)

式中：φm(m=1,2,…,p)是自回归模型的系数；θj(j=1,2,…,q)为平均滑动系数；at为白噪声序列。

1.2 ARIMA模型参数的判定

1.2.1差分化

为了确定非平稳时间序列中d的取值，对时间序列进行差分化。当时间序列的自相关系数(ACF)和偏相关系数(PACF)的序列值趋于稳定时，此时序列是平稳的，否则为非平稳，对于非平稳的时间序列需要通过d次差分得到平稳序列，此时，ACF和PACF趋于稳定且无显著地非零，确定模型的差分阶数为d。

1.2.2p、q值的确定

确定适合的p、q值，一般通过使用贝叶斯信息准则(BIC)[4]或赤迟信息量准则(AIC)[5]，两种准则相比，贝叶斯准则的收敛效果更好，而赤迟信息准则的稳健性较强，对于模型中可能出现的过度敏感的情况可以较好的解决，基于此，可以根据建模的具体情况选择合适的准则，确定模型阶数，从而模型确定。

2 基于实时跟踪的ARIMA模型

2.1 实时跟踪算法对ARIMA模型的优化

在ARIMA模型中，模型阶数的选择对模型拟合及预测的精度的影响较大，为了保证拟合的精度，有时会选择较高阶的模型参数，然而阶数较高会对模型预测长度有所限制。因此，为了在保证模型精度的前提下，提高模型的预测长度，提出使用实时跟踪算法对原ARIMA模型进行优化。

实时跟踪算法的主要思想即等维递补的思想[6]，假设时间序列{x1,x2,…,xn}，对该时间序列建立ARIMA模型，预测模型的预测步长为k，即通过模型对n个实测值进行拟合来预测n时刻后的值{xn+1,xn+2,…,xn+k}，由于时间序列{x1,x2,…,xn}是不断更新的，即可以获得之后的k个实测数据，此时将最开始的k个数据去除，即{x1,x2,…,xn}，用之后获得的k个数据补充到时间序列中，此时，更新的时间序列为{xk+1,xk+2,…,xk+n}，对更新的时间序列重新建立ARIMA模型，进行下一步的预测，保持时间序列等维，以此类推，不断加入最新的实测数据，去除旧数据，构成了动态预测的ARIMA模型群，即为等维递补预测模型。

2.2 基于实时跟踪的ARIMA模型建模步骤

大坝变形的监测量一般为非平稳的时间序列，建立基于实时跟踪的ARIMA的大坝变形监控模型建模流程如下：

步骤1。对时间序列进行平稳性检验，得到差分阶数d，首先，初步判断时间序列的平稳性，可以通过时间序列的折线图初步估计，然后通过相关图法以及ADF单位根检验判断序列的平稳性，对不平稳的时间序列，通过差分变换进行平稳化，得到差分次数d。

步骤2。模型的定阶，即确定模型的p、q值。本文采用BIC准则(贝叶斯准则)[8]确定模型中的p、q值。其表达式为：

(2)

式中：N为样本总数；σ2k为方差的估计。

步骤3。模型的阶数确定后，可以通过统计学的相关方法计算得到模型参数[7]，比如最小二乘，矩阵估计等，得到参数后，检验at是否为白噪声序列，不是则必须再次估计，直到at满足要求，完成ARIMA模型的建立。

步骤4。使用建立好的模型对大坝变形数据进行拟合预测。即通过前n个实测值预测未来k个时刻的变形值。

步骤5。对时间序列进行等维递补，即加入最新实测的k个变形值，去除最前的k个变形值，保持时间序列的长度不变，建立新的ARIMA预测模型。以此类推，不断更新数据，得到动态预测的ARIMA模型群，直到预测长度满足预测要求。

基于实时跟踪的ARIMA模型流程图如图1。

图1 组合模型的计算流程Fig.1 Calculation flow chart of combined model

3 工程实例

本文以国内某水电站枢纽为例，该坝为混凝土双曲拱坝，通过布置正垂线对大坝进行监测，选取该大坝坝顶某点2012年7月1日-8月15日46组的原始位移观测值，将这些数据分为两部分：前40组数据用于建模拟合；后6组数据用于预测，检验模型的精度。该大坝位移测点的时间序列，如图2。

图2 大坝变形实测值时间序列Fig.2 Time serious of dam deformation

对该时间序列进行平稳性分析，分析ACF和PACF值的变化趋势，未差分前的值如图3所示。

图3 大坝变形实测值的ACF和PACF系数Fig.3 ACF and PACF coefficients of dam deformation

由图3可见，该序列的ACF值和PACF值的大多数都超出了置信区间，为不平稳的时间序列，因此，对原序列进行一次差分计算，差分后的时间序列见图4，差分后的ACF系数和PACF系数见图5。

图4 大坝变形实测值一次差分序列Fig.4 First difference serious of dam deformation

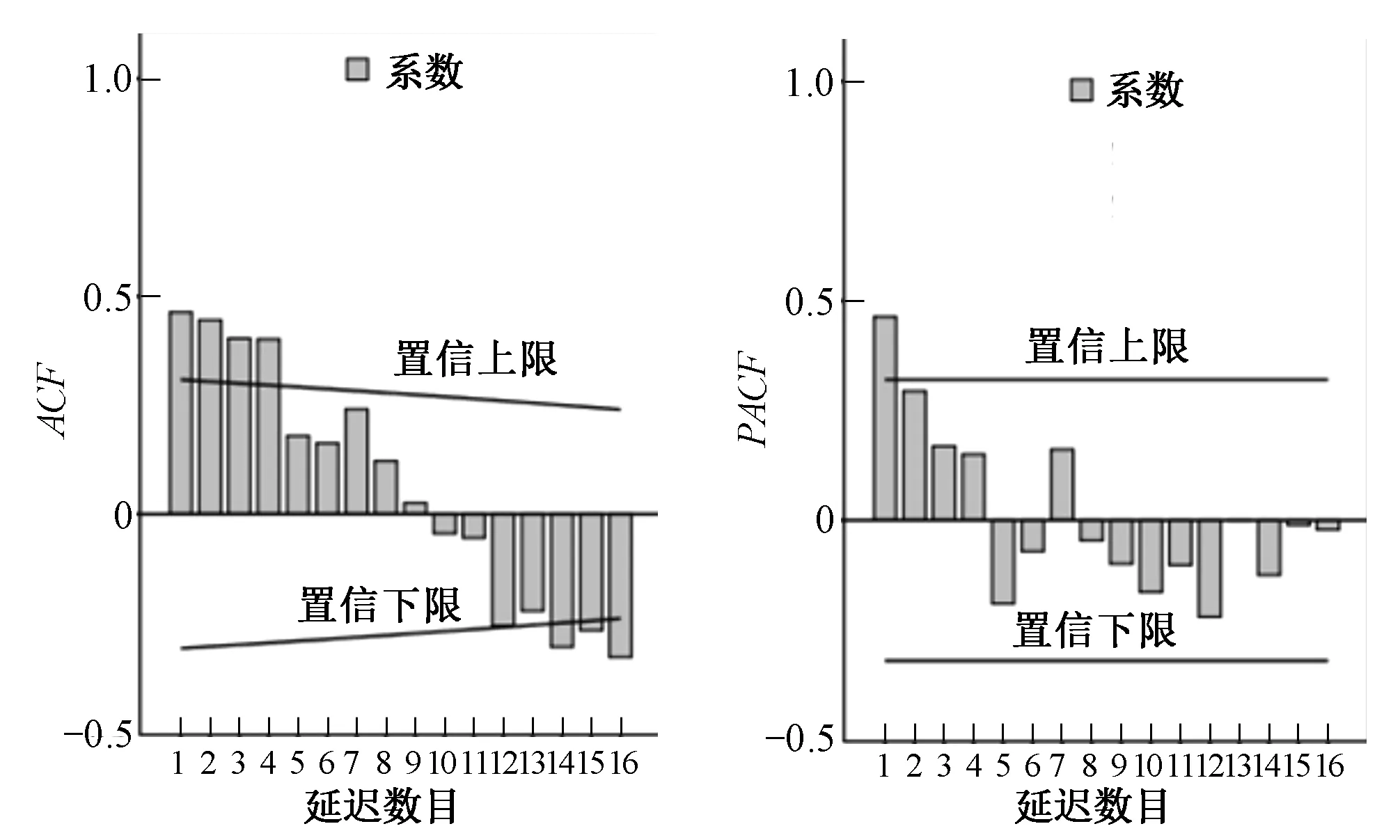
图5 大坝变形实测值一次差分序列的ACF和PACF系数Fig.5 ACF and PACF coefficients of first difference series of dam deformation

经过一次差分，可见大坝变形的一次差分序列围绕某值上下波动且趋于稳定，ACF系数和PACF系数的波动也在置信区间范围内，因此，认为原序列一次差分后为平稳序列，基于此，d定为1。

确定差分次数d后，使用BIC准则确定模型阶数，从低阶到高阶依次计算BIC值，具体计算结果见表1。

表1 模型的BIC准则值Tab.1 BIC guideline values of model

由表1可知，p=4,q=4时BIC值最小，故该ARIMA模型的p值取4，q值取4，即建立ARIMA(4，1，4)模型，对实测数据进行拟合及预测，拟合曲线见图6，计算拟合及实测值的残差序列，如图7。

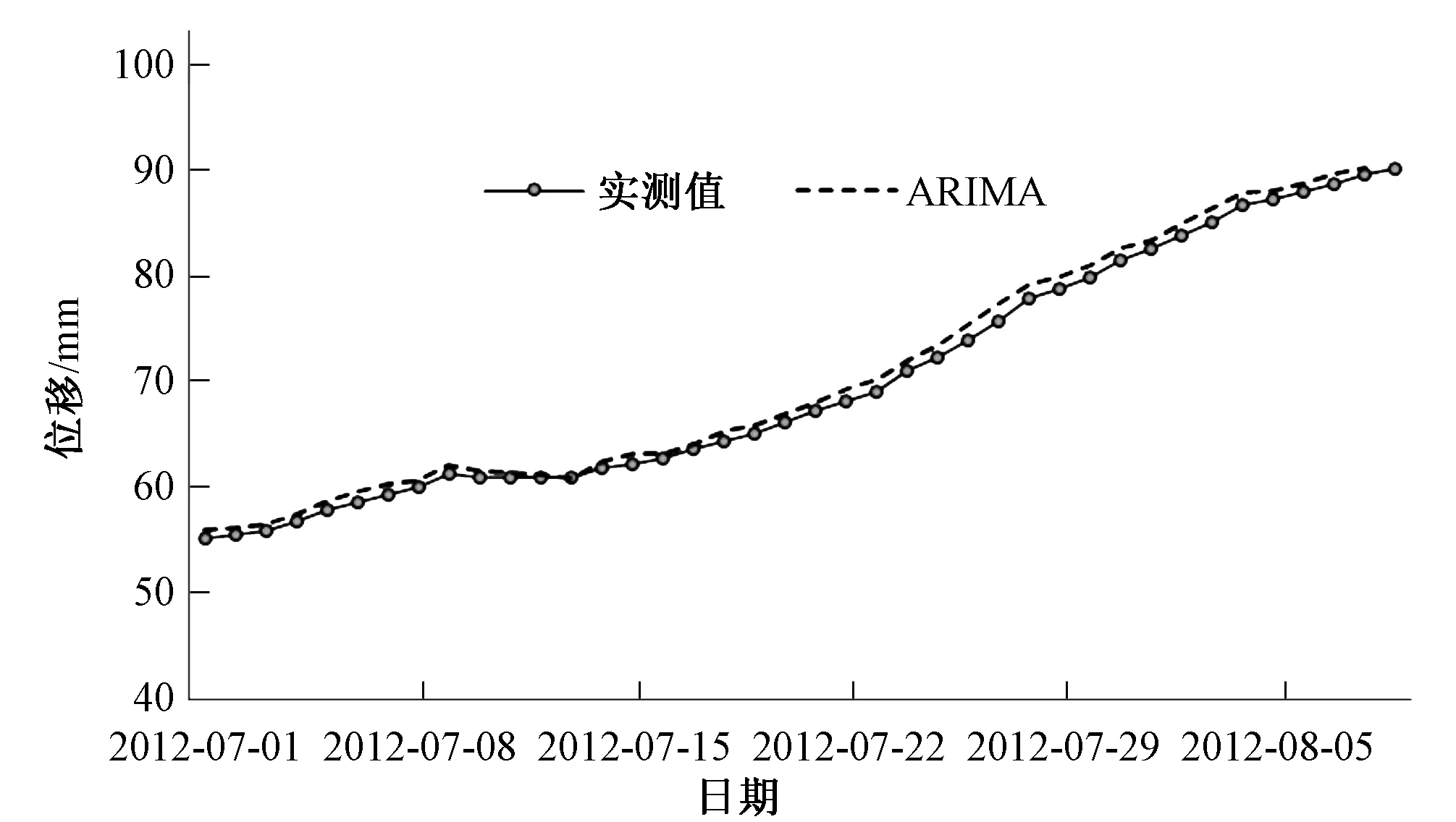
图6 拟合模型比较图Fig.6 Comparison chart of prediction models

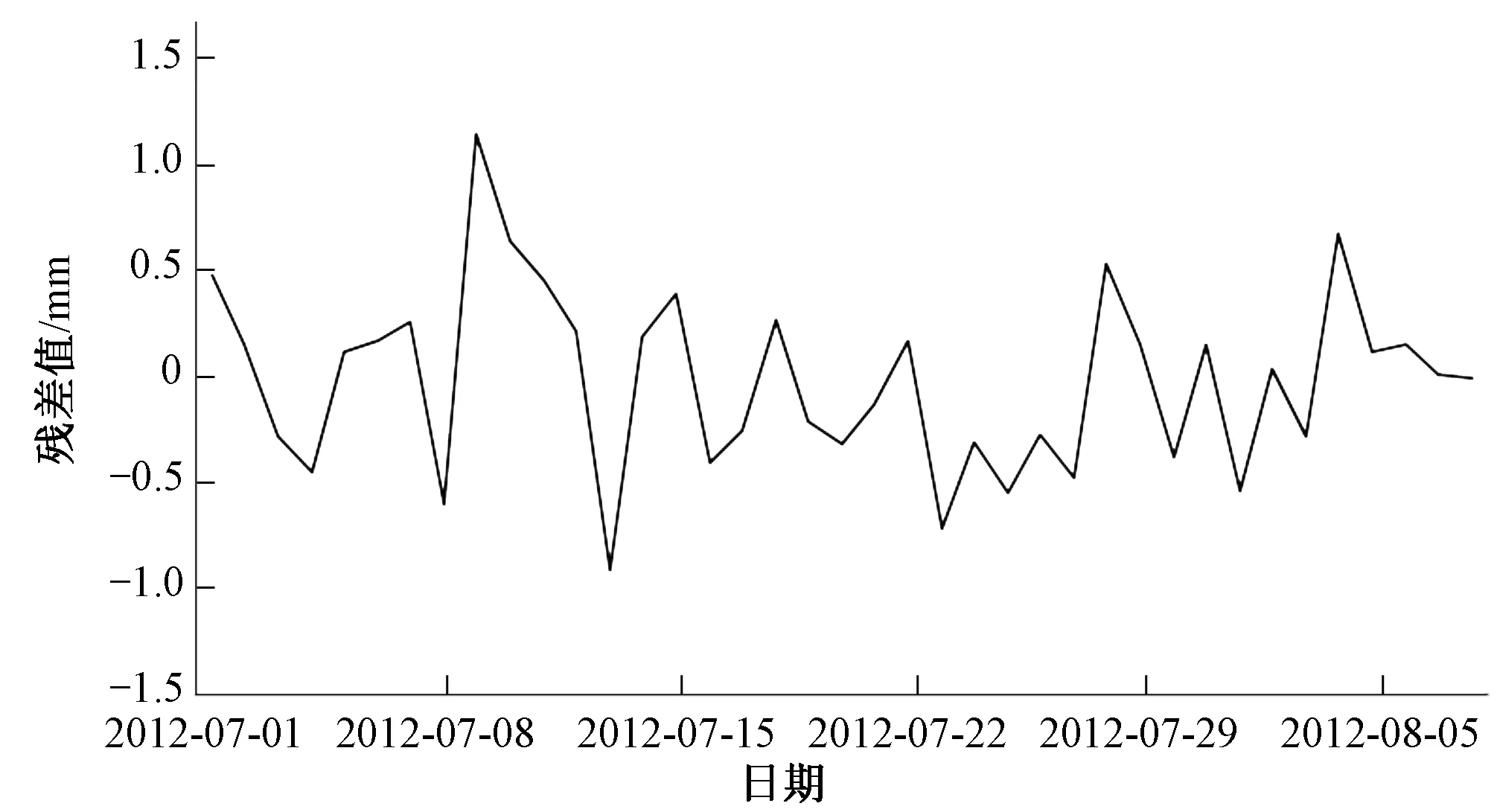
图7 ARIMA模型与原监测数据的拟合残差值Fig.7 Fitting errors of ARIMA model

为了保证拟合的精度，在选择模型阶数时选值较大，由图7可以看出，拟合的残差值都在1.5 mm内，精度较高，但是该模型却对预测的长度有所限制，为了在保证模型精度的同时增加预测的长度，采用实时跟踪算法对ARIMA模型进行优化，设定模型的预测步长为1，对未来6天的变形值进行预测，将时间序列进行等维递补，保持时间序列的长度不变，建立动态预测的ARIMA模型群。将优化模型与原模型的预测结果进行比较，见表2。

由表2可以看出，基于实时跟踪的ARIMA模型相对ARIMA模型在预测精度上有所提高，更能反

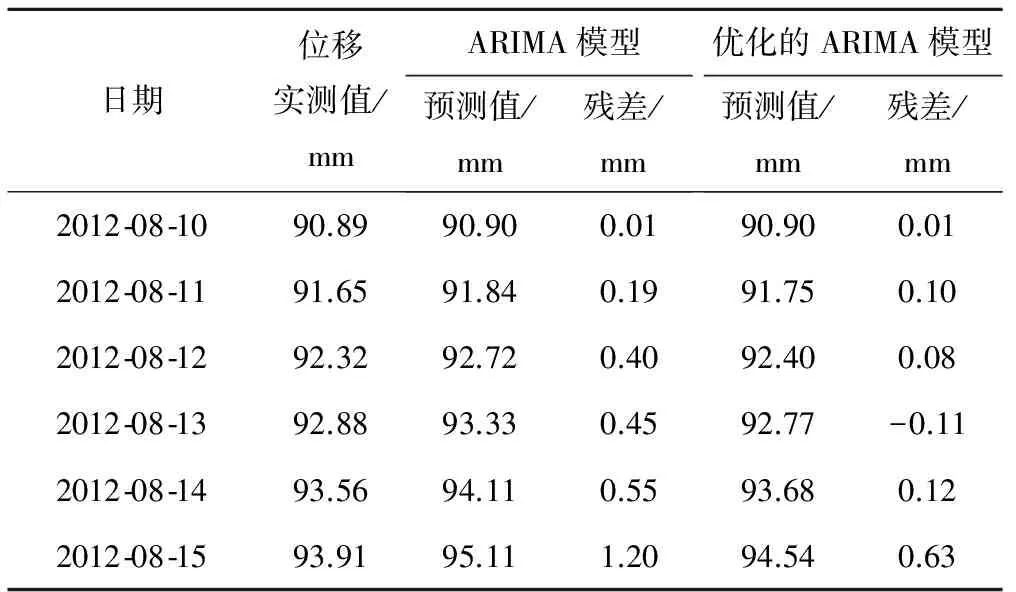
表2 两种模型的预测结果对比Tab.2 Two predicted values and the relative errors of the model

映出大坝变形的实际情况，同时优化后的模型对于预测长度的局限性较小，可以进行步长较长的变形预测。

4 结 语

本文在ARIMA模型的基础上，使用实时跟踪算法对模型进行优化，建立基于实时跟踪的ARIMA模型，并应用到大坝安全监测中。以某水利工程的变形监测数据作为研究对象进行建模，与原ARIMA模型相比精度有所提高，预测结果较好，更能反映大坝安全性态，同时具有较长的预测步长，其等维递补的思想充分利用了数据的动态信息，值得用于较为复杂的大坝变形安全监控及预报中。

□

[1] 顾冲时,吴中如.大坝与坝基安全监控理论和方法及其应用[M]．南京：河海大学出版社,2006．

[2] Su Huaizhi，Wen Zhiping，Wu Zhongru.Study on an Intelligent Inference Engine in Early-warning System of Dam Health[J]．Water Resources Management,2011,25(6):1 545-1 563.

[3] 李经纬,包腾飞.基于ARIMA-GRNN模型在大坝安全监测中的应用[J].水电能源科学,2013,31(7)：48-50.

[4] 王 锋,苏怀智,荆 凯.基于ARIMA-ANN的大坝监控模型[J].武汉大学学报,2010,43(5)：585-588.

[5] 魏武雄.时间序列分析-单变量和多变量方法[M].2版.北京：中国人民大学出版社，2009.

[6] 钱龙霞,刘明国,黄占峰,等.基于自相关性分析的等维灰数递补动态预测模型及其应用[J].北京师范大学学报(自然科学版),2008,44(6)：640-644.

[7] 苏怀智，温志萍，吴中如.基于SVM理论的大坝安全预警模型研究[J]. 应用基础与工程科学学报，2009,17(1):40-48.