一种新的地下滴灌毛管水力计算模型
——基于土壤初始含水率和土壤黏粒含量空间变异性研究
侯 雯,寇飞周,周颖明(陕西华地勘察设计咨询有限公司,西安 710018)
地下滴灌是把灌水毛管及其灌水器埋入土壤中,将水或水肥的混合液缓慢渗入到作物根区土壤,再借助毛细管作用或重力作用将水分扩散到根系层供作物吸收利用的一种灌水方法[1,2]。
王晓愚[3]等以灌水器工作压力、土壤初始含水率和土壤容重为影响因素,在试验的基础上,建立了地下滴灌灌水器流量计算经验公式,但公式经验参数是针对某一种土壤试验获得的。其实对不同质地的土壤,地下滴灌灌水器的流量大小也不尽相同[4]。Lazarovitch et al.[5]基于正压地下滴灌灌水器稳定流量计算公式[6]和毛管的沿程水头损失计算公式相结合,同时考虑了土壤的空间变异性,提出了地下滴灌毛管水力计算方法,这一方法首次考虑了土壤空间变异性对地下滴灌毛管水力要素的影响,但其中反映土壤空间变异性的有关参数是随机生成的,因此这一方法缺乏试验验证。Gil et al.[7]在试验的基础上,综合考虑了滴头制造偏差等因素,提出了地下滴灌毛管水力计算方法,这一方法具有一定的试验基础,但试验装置与工程实际相差太大。
滴头埋于土中,地下滴灌毛管水力要素的空间分布必然受到土壤物理要素的影响,因此土壤的空间变异性会影响地下滴灌毛管水力要素的空间分布规律。本文以此为研究目的,结合试验建立空间变异性影响下的地下滴灌毛管水力要素计算模型。为揭示土壤空间变异性和地下滴灌毛管水力特性的内在联系,地下滴灌系统的规划、设计、管理和产品开发提供理论依据。
1 地下滴灌条件下土壤物理参数的空间变异性
1.1 试验方案
试验区位于北京市平谷区东高村镇的东高村,试验布置如图1所示。

图1 试验布置示意图Fig.1 Experimental arrangement diagram
试验区地下水埋深为83 m,采用机井作为灌溉水源。试验地块为200 m×35 m大小。支管和毛管的埋深均为0.4 m。支管选用φ60PE管,毛管(滴灌管)选用φ16PE管,支管两侧各布置8条毛管,毛管长度为100 m,毛管上滴头间距为0.3 m,毛管之间的间距为5 m。压力表用来测量毛管进口处压力值,水表用来测量毛管进口处水量,根据灌水时间,可计算得出毛管入口处流量值。土壤初始含水率和土壤黏粒含量测定沿着毛管铺设方向从右往左进行。沿着毛管方向每隔5 m设置一个取样点,在取样点土壤表层下深度为60 cm处取土样,采用烘干法[8]测定土壤初始含水率;沿着毛管方向每隔5 m设置一个取样点,在每个取样点土壤表层下深度30、60、90 cm取土样,采用激光粒度仪[9]测定土壤颗粒级配。对该试验地块的土壤初始含水率和土壤颗粒级配的取样值进行统计特征分析和空间分布特征分析,探求整片试验地块上土壤初始含水率和土壤黏粒含量的空间分布格局,为研究土壤物理参数(土壤初始含水率和土壤黏粒含量)空间变异性对地下滴灌毛管水力特性的影响奠定基础。
1.2 土壤物理参数的统计特征分析
采用SPSS19.0软件包K-S检验[10]或z的标准正态Q-Q图[11]来分析土壤初始含水率和土壤黏粒含量在土壤中分布的正态性。根据SPSS软件对样本均值及标准差的分析来确定各因素的变异性质。
1.2.1土壤初始含水率的统计特征分析
按经典统计方法对土壤初始含水率的统计特征值进行分析:剔除异常点后的样本数为308个,土壤初始含水率的变化范围为12.43%~23.74%,其平均值为17.34%。土壤初始含水率的变异系数为11.31%,属于中等变异[12]的范围。土壤初始含水率用K-S正态分布检验概率(PK-S)[13]进行检验,取显著水平α=0.05,土壤初始含水率PK-S=0.200>0.05,符合标准正态分布,满足地质统计学方法分析的前提。
1.2.2土壤黏粒含量的统计特征分析
选用0.01 mm以下粒径的颗粒作为研究对象[14]。对不同取样点处各深度土样的黏粒含量测定结果取平均值进行分析。土壤黏粒含量的样本数为327个,变化范围为19.33%~60.71%,平均值为39.25%。土壤黏粒含量的变异系数为21.27%,属于中等变异的范围。
根据K-S检验,土壤黏粒含量不符合标准正态分布。对其进行对数转换,经对数转换后,消除了可能存在的比例效应。经对数转换后的数据进行K-S值检验,土壤黏粒含量对数转换后的PK-S=0,仍不满足标准正态分布。采用标准正态Q-Q图来检验数据的正态性,若样本数据近似于正态分布,在标准Q-Q图上这些点近似成一条直线,由图2所示可知,土壤黏粒含量取对数后满足近似正态分布。
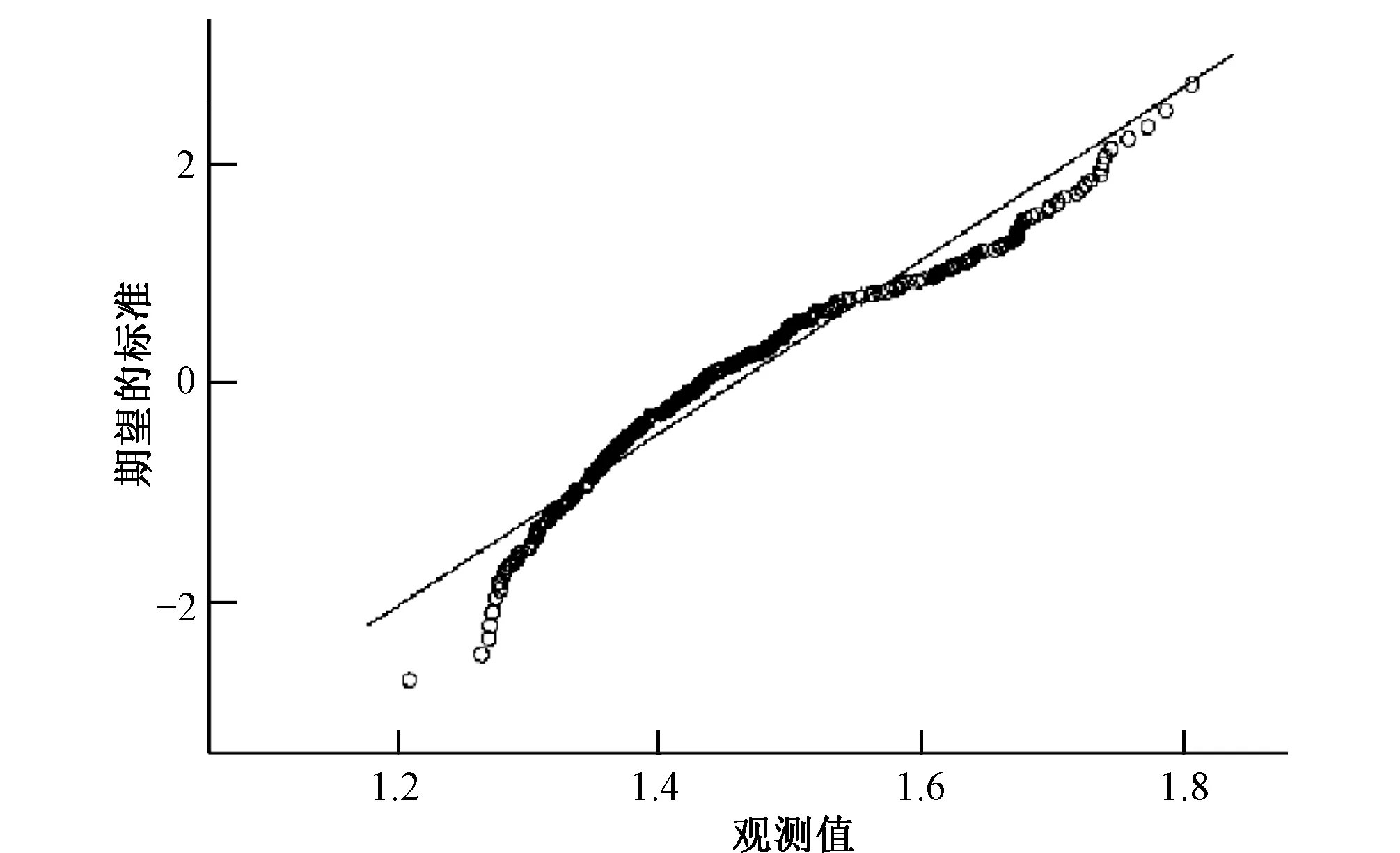
图2 土壤黏粒含量对数转换后标准Q-Q图Fig.2 Standard Q-Q plot of soil clay content after natural logarithmic transformation
1.3 土壤物理参数的空间分布特征分析
在GS+ 9.0平台上,土壤初始含水率、土壤黏粒含量分别用线性、球状、高斯和指数等理论模型进行拟合,根据拟合误差大小选出最适模型,得出土壤物理参数的半方差函数。用普通克里格法(Ordinary Kriging)内插获得空间变异分布图。通过Kriging插值图进行土壤物理参数空间变异特征的分析。
1.3.1土壤初始含水率的空间分布特征分析
经检验,土壤初始含水率服从标准正态分布,可直接进行半方差函数模型的拟合。其变异函数理论模型和拟合参数如表1所示。
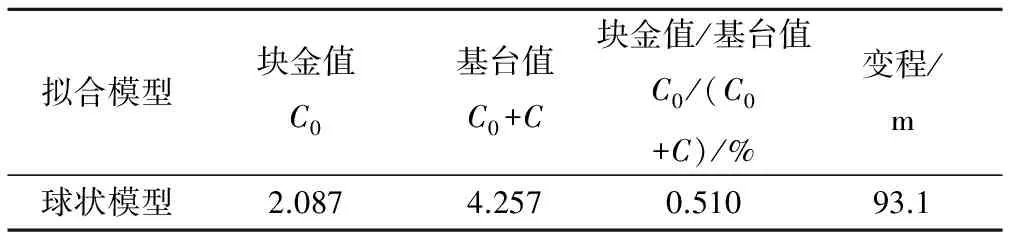
表1 土壤初始含水率变异函数理论模型拟合参数Tab.1 Semivariogram theoretical models and contents and fitting parameters of the soil initial moisture content
土壤初始含水率的块金系数为0.510,说明其具有中等的空间相关性[15]。
1.3.2土壤黏粒含量的空间分布特征分析
经检验,土壤黏粒含量经过对数转换后满足近似正态分布,因此可进行半方差函数模型的拟合,其变异函数理论模型拟合参数见表2。
土壤黏粒含量经过对数转换后的半方差函数理论模型的块金系数为0.640,具有中等的空间相关性。

表2 土壤黏粒含量变异函数理论模型拟合参数Tab.2 Semivariogram theoretical models and contents and fitting parameters of the soil clay content
图3、图4分别为土壤初始含水率和对数转换后的土壤黏粒含量的空间分布插值图。
2 地下滴灌毛管水力要素研究
2.1 地下滴灌毛管上单滴头公式的建立
考虑土壤初始含水率和土壤黏粒含量的空间变异性,建立单滴头公式如下:
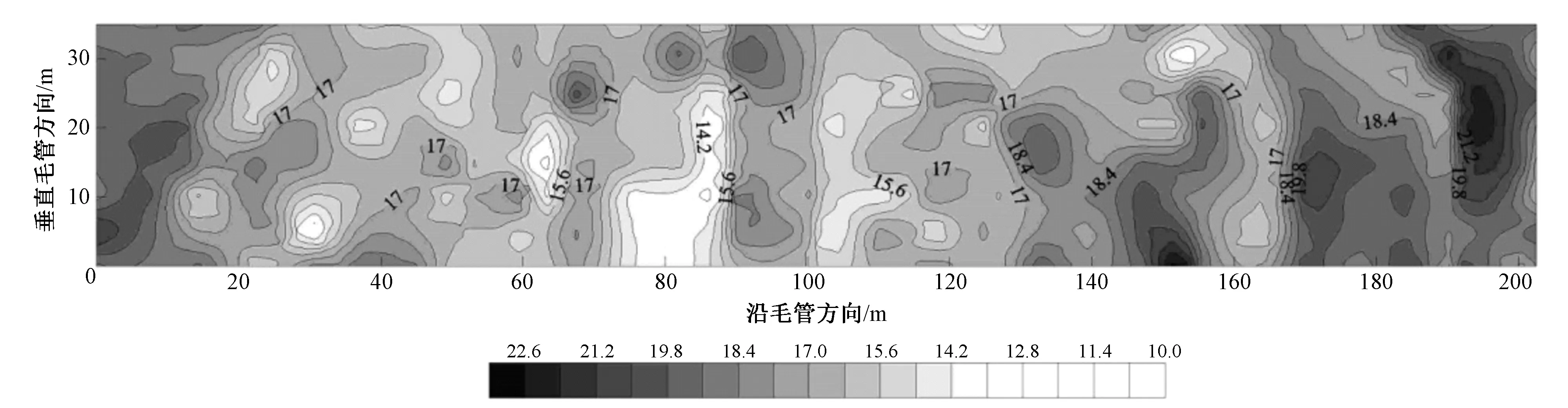
图3 土壤初始含水率(%)的Kriging插值图Fig.3 Kriging interpolation map of the soil initial moisture content(%)

图4 对数转换后的土壤黏粒含量(%)的Kriging插值图Fig.4 Kriging interpolation map of the soil clay content after natural logarithmic transformation(%)
qi=kHxiθaiMbi
(1)
式中:qi为地下滴灌毛管上第i个滴头流量,L/h;Hi为地下滴灌毛管上第i个滴头压力,m;θi为地下滴灌毛管上第i个滴头处土壤初始含水率(重量),%;Mi为地下滴灌毛管上第i个滴头处土壤黏粒含量,%;k为经验系数;a、b和x为经验指数。
2.2 地下滴灌毛管水力要素计算模型的建立
地下滴灌毛管沿程压力水头分布如图5所示。毛管上有n个滴头,0点为毛管入口,在毛管入口处安装水表和压力表,可测得毛管入口流量Q0和入口端压力H0。
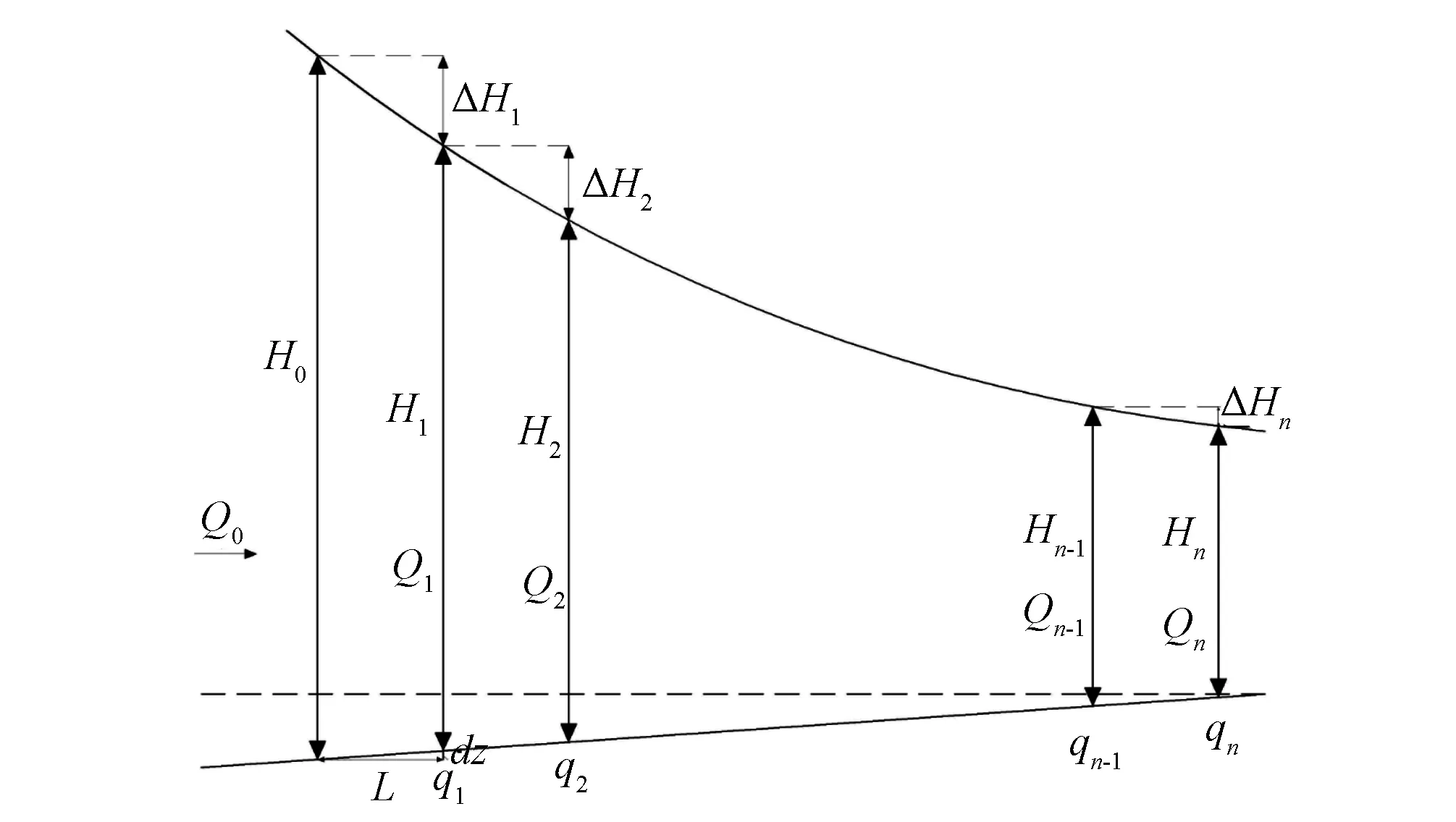
图5 毛管上沿程压力水头分布示意图Fig.5 Pressure head distribution of along multiple-outlet pipeline
将毛管从入口0处开始按滴头位置分为n个管段,由能量方程可知对于第i段管段有:
平台功能:1)检索,提供标题、关键词、长词等检索,通过语义分析给予最符合的检索结果,并在详情页推荐相似文献;II)订阅服务,读者可根据作者、主题、关键字或出版标准来选择出版物提醒服务。
Hi-1+dZ-ΔHi-Hi=0
(2)
由图5和式(2)可列出毛管上各管段能量方程组成的非线性方程组:
(3)
dz=IL
(4)
式中:Hi为毛管上第i个滴头处的压力水头,m;dZ为相邻滴头的高差,m;ΔHi为第i段管段的水头损失,m;I为地面坡度,I<0为上坡,I=0为平坡,I>0为下坡;L为相邻滴头的间距,m。
管道水头损失由沿程水头损失和局部水头损失组成。沿程水头损失可按下式进行确定:
(5)
式中:hf为管道沿程水头损失,m;f为摩阻系数,毛管为聚乙烯管,管径16 mm,查规范[16],f=0.505;Q为管道流量,L/h;D为管道内径,mm;L为管段长度(本处即指滴头间距),m;m为流量系数,毛管为聚乙烯管,管径16 mm,查规范[16],m=1.75;B为管径指数,毛管为聚乙烯管,管径16 mm,查规范[16],B=4.75。
管道的局部水头损失可按沿程水头损失的一定比例估算。因此,管段水头损失的计算可按下式确定:
ΔH=αhf
(6)
式中:α为毛管局部水头损失加大系数。
将式(5)代入式(6),即可得各管道水头损失计算公式:
(7)
(8)
式中:Qi为毛管第i段管段流量,L/h;qi为毛管上第i个滴头的流量,L/h。
由式(1)可得:
(9)
将式(7)~(9)和(4)代入式(3)中,即可建立在考虑土壤空间变异性的条件下毛管水力要素计算的数学模型。
(10)
毛管坡度I、毛管管径D、滴头个数n、滴头间距L已知,毛管上各滴头处土壤初始含水率和土壤黏粒含量的数据可通过Kriging插值得出,毛管进口处压力H0由试验测得。式(10)是一个由333个方程组成的非线性方程组,可求解333个滴头流量qi,通过式(9)也可以求解毛管上的沿程压力值。
2.3 地下滴灌毛管水力要素计算模型参数求解
毛管水力要素计算数学模型中,除滴头流量qi外,a、b、x、k、α也为未知量。为求解模型中的相关未知参数,可将其转化为目标函数的优化问题。以Matlab遗传算法工具箱[17]为主要工具,解决有约束的最优化问题。
根据试验方案,毛管的进口流量值已知,因此可建立目标函数为:毛管进口流量的均方差最小。即:
(12)
式中:j为用来求解模型中参数的毛管条数;Q0计算为模型计算得出的毛管进口流量值,即模型计算后所得毛管上所有滴头流量之和;Q0为试验测得的毛管进口流量值;n为每条毛管上的滴头总个数;qi为滴头流量值,由毛管水力要素计算数学模型求解得出。
目标函数的求解与参数a、b、x、k、α的取值有关。假设已知a、b、x、k、α的取值范围,则目标函数是寻找一组最优的(a,b,x,k,α)的组合,使得毛管进口流量的均方差达到最小。
根据相关文献[18],可用a、b、x、k和α这5个参量的上下限来约束目标函数的值,令目标函数达到最小。a、b、x、k和α这5个参量的上下限取值如表3所示。

表3 优化变量上下限取值Tab.3 The upper and lower bounds of optimizing variables
对14组毛管试验数据通过遗传算法进行迭代,可求出a、b、x、k、α这5个参量的最优解如表4所示。

表4 优化参量最优解Tab.4 optimal solution of optimizing variables
为验证模型的可靠性和正确性,将优化目标函数的方法求得的参量a、b、k、x、α代入模型计算得出毛管入口流量Q0计算,通过比较试验测量值Q0和模型计算值Q0计算的大小,利用另外2组毛管的试验数据进行校核和验证。对比结果如表5所示。

表5 地下滴灌毛管水力要素试验结果与水力计算模拟结果Tab.5 Experiment and simulation results of hydraulic calculation of the lateral under SDI
通过比较可知,入口流量试验值Q0与入口流量计算值Q0计算之间的误差较小,说明根据试验建立的地下滴灌毛管水力要素计算模型式(10)是正确的。因此可确定考虑土壤物理参数(土壤初始含水率和土壤黏粒含量)空间变异性条件下的地下滴灌滴头流量计算公式:
qi=0.520 1H0.583 7θ-0.040 4M-0.077 8
(13)
3 结 语
(1)经统计特征分析,土壤初始含水率和土壤黏粒含量均属于中等变异的范围;由半方差函数分析可知,土壤初始含水率和土壤黏粒含量均符合球状模型,且均具有中等相关性的空间分布特征。通过Kriging插值可以直观地反映土壤初始含水率和土壤黏粒含量的空间分布情况。
(2)考虑土壤物理参数(土壤初始含水率和土壤黏粒含量)的空间变异性,建立单滴头公式。通过分析地下滴灌毛管沿程压力水头和流量分布情况,根据地下滴灌毛管管段能量方程建立考虑土壤物理参数空间变异性的地下滴灌毛管水力要素计算模型。
(3)采用MATLAB遗传算法工具箱迭代求解地下滴灌毛管水力要素计算模型中的未知参数a、b、x、k、α的最优解,进而运用MATLAB非线性方程组数值解法编程求解毛管上的滴头流量,从而得出毛管入口流量。比较毛管入口流量的实测值和计算值,由于相对误差较小,实测值和计算值较吻合,说明建立的地下滴灌毛管水力要素计算模型较为合理。
□
[1] 寇 丹,苏德荣,吴 迪,等.地下调亏滴灌对紫花苜蓿耗水、产量和品质的影响[J].农业工程学报,2014,30(2):116-123.
[2] Patel N, Rajput T B S. Dynamics and modeling of soil water under subsurface drip irrigated onion[J]. Agric. Water Manage., 2008,95(12):1 335-1 349.
[3] 王晓愚,白 丹,李占斌,等.土壤物理特性对地下滴灌灌水器流量影响分析[J].干旱区资源与环境,2009,23(3):126-129.
[4] Gil M, Rodríguez-Sinobas L, Sánchez R, et al. Procedures for determining maximum emitter discharge in subsurface drip irrigation[J]. J. Irrig. Drain Eng., 2011,137:287-294.
[5] Lazarovitch N, Shani U, Thompson T L, et al. Soil hydraulic properties affecting discharge uniformity of gravity-fed subsurface drip irrigation systems [J]. ASCE, Journal of Irrigation and Drainage Engineering, 2006,132(6):531-536.
[6] Warrick A W., Shani U. Soil-limiting flow from subsurface emitters. II: effect on uniformity[J].J. Irrig. Drain. Eng. ASCE,1996,122(5):296-299.
[7] Gil M, Rodriguez-Sinobas L, Juana L, et al. Emitter discharge variability of subsurface drip irrigation in uniform soils: Effect on water-application uniformity [J]. Irrigation Science,2008,26(6):451-458.
[8] 陈立新. 土壤实验实习教程[M].哈尔滨:东北林业大学出版社,2005.
[9] 程 鹏,高 抒,李徐生.激光粒度仪测试结果及其与沉降法、筛析法的比较[J].沉积学报,19(3):449-455.
[10] Burgess T M, Webster R. Optimal interpolation and isarithmic mapping of soil properties. I. The semivariogram and punctual Kriging[J]. Soil Sci., 1980,(31):315-331.
[11] 陈翠英,江永真,袁朝春.土壤特性空间变异性研究[J].农业机械学报,2005,36(10):121-124.
[12] 洪 楠.Statistic for Windows 统计与图表分析教程[M].北京:清华大学出版社,2002:152-159.
[13] 王政权.地质统计学及在生态学中的应用[M]. 北京:科学出版社,1999.
[14] 龚振平.土壤学与农作学[M]. 北京:中国水利水电出版社,2008.
[15] 古丽娜尔·托尔提,海米提·依米提,米日姑·买买提,等.伊犁河谷土壤含盐量空间变异和格局分析[J].干旱地区农业研究,2011,29(2):152-158.
[16] GB/T 50485-2009,微灌工程技术规范[S].
[17] 吴祈宗.运筹学与最优MATLAB编程[M]. 北京:机械工业出版社,2009:195-205.
[18] 李 刚,王晓愚,白丹.地下滴灌中毛管水力计算的数学模型与试验[J].排灌机械工程学报,2011,29(1):87-92.

