《3-4》光学热点问题归类讲解

新疆 张 帆

《3-4》光学热点问题归类讲解

新疆 张 帆

从变化的情景中找出共性的东西并解决更多的新问题是二轮复习的终极目标。

高考对教材《3-4》的计算题命题，常常围绕光的折射定律和全反射规律的综合应用进行，鉴于三个选修试题的平衡，难度适中，所以复习时要重点问题重点解决。从近两年得分情况看，有一定的提升，在2016年的高考复习中，更应该保持这种势头。那么，哪些要点必须要掌握呢？且看下文。

一、利用三棱镜对光的作用考查学生对几何光学规律的综合应用

【例1】（2015·黑龙江大庆三检）如图1所示，某透明介质的截面为直角三角形ABC，其中∠A＝30°，AC边长为L，一束单色光从AC面上距A为的D点垂直于AC面射入，恰好在AB面发生全反射。已知光速为c。求：

图1

（1）该介质的折射率n；

（2）该光束从射入该介质到第一次穿出经历的时间t。

【解析】（1）由于光线垂直于AC面射入，故光线在AB面上的入射角为30°

由题意知，光线恰好在AB面上发生全反射

全反射的临界角C＝θ＝30°

【总结】近年高考中，涉及几何光学问题大多以全反射有关，解决全反射问题的一般方法：

（1）确定光是从光密介质进入光疏介质。

（3）根据题设条件，判定光在传播时是否发生全反射。

（4）如发生全反射，画出入射角等于临界角时的临界光路图。

（5）运用几何关系或三角函数关系以及反射定律等进行分析、判断、运算，解决问题。

二、利用球型玻璃砖对光的作用考查学生对几何光学规律的综合应用

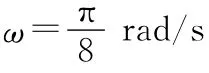
（1）当玻璃砖由图示位置转动多长时间屏上光斑刚好彻底消失；

（2）玻璃砖由图示位置转到光斑刚好彻底消失的过程中，光斑在屏上移动的距离s。

图3

【解析】（1）由题意可知，假设玻璃砖转过θ角时，折射光线刚好完全消失。此时的入射角也为θ，由折射定律可得

解得r＝0°

由图4可知在玻璃砖逆时针转过θ角过程中折射光线顺时针转过α角

图4

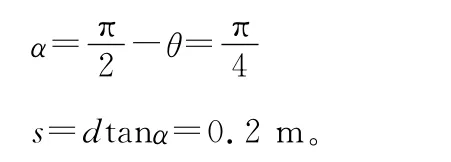
【答案】（1）2s （2）0.2m

【点悟】球形玻璃砖问题主要涉及两个方面，一个是利用球面的几何关系考查学生数理结合能力，另一个是利用球面解决一些实际问题，如虹、霓等，此类问题一般都会涉及全反射现象的发生，所以审题时一定要仔细要认真分析。忽视全反射是此类问题的最大错误，由于全反射现象的出现，有些试题会对应临界问题。另外利用球形玻璃砖测定折射率实验也要理解原理。

三、利用平行玻璃砖对光的作用考查学生对几何光学规律的综合应用

【例3】如图5所示，含有两种单色光的一细光束，以入射角θ射入厚度为d的平行玻璃砖中，该玻璃砖对两种单色光的折射率分别为n1和n2，且n1＞n2。求两束单色光从下表面射出时出射点之间的距离。

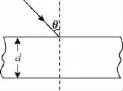
图5

【解析】光路图如图6所示，

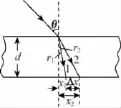
图6

【引申】若光从平行玻璃砖上表面射入，从下表面射出，出射光线与入射光线平行，整个过程不会发生全反射，所以利用平行玻璃砖测定光的折射率成为首选。另外就计算而言出射光与入射光有一定的偏移，那么，偏移距离为多少？不同的射光以相同的入射角射入平行玻璃砖的上表面，比较各种色光在玻璃砖中传播的时间或根据光路分析各种色光的其他特性，如干涉条纹、临界角等问题要融会贯通。

即时演练

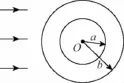
1.用折射率为n的透明介质做成内、外半径分别为a和b的空心球，如图所示，当一束平行光射向此球壳，经球壳外、内表面两次折射后，能进入空心球壳的入射平行光线的横截面积是多大？

参考答案及解题提示

1.πa2

【解析】设入射光线EF为所求光束的临界光线，入射角为i，经球壳外表面折射后折射角为r有

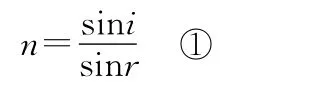
因为EF为临界入射光线，所以该光线射向内表面的入射

角正好等于临界角c，有

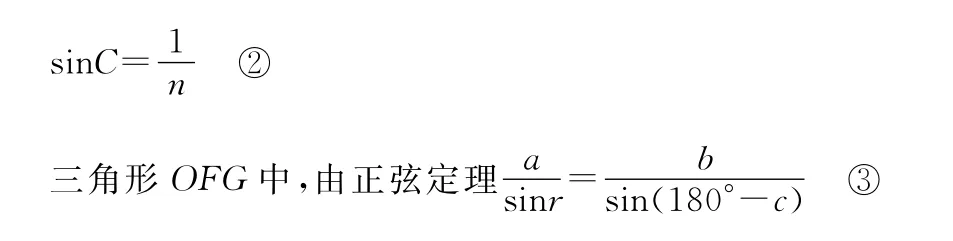
根据对称性可知，所求光束的截面S应是一个圆，设圆半径R，因为入射光为平行光

所以R＝b·sini⑤

由④⑤得R＝aS＝πR2＝πa2。

所以光在玻璃砖内发生5次全反射，光路如图所示

（作者单位：新疆乌鲁木齐市高级中学）