分瓣式内卡瓦有限元分析及结构参数优化设计

李英松，李克鹏，边 杰，周先军，李 标

（1.中海油田服务股份有限公司完井中心，天津300450；2.中国石油大学（华东）机电工程学院，山东青岛266580）



分瓣式内卡瓦有限元分析及结构参数优化设计

李英松1，李克鹏2，边 杰1，周先军2，李 标2

（1.中海油田服务股份有限公司完井中心，天津300450；2.中国石油大学（华东）机电工程学院，山东青岛266580）

摘要：以分瓣式内卡瓦力学性能为研究目标，以卡瓦锥角γ、牙倾角α、螺距d及螺纹啮合深度h为参数，采用ANSY S有限元分析法及正交试验法对内卡瓦结构进行参数优化设计。通过极差法和方差法对试验结果进行分析，得出卡瓦锥角和螺距为影响其力学性能的显著性因素。当γ、α、d和h分别取6°、20°、2.5mm和0.5mm时，卡瓦力学性能最优。

关键词：分瓣内卡瓦；有限元分析；正交优化；结构参数

内卡瓦作为支撑封隔器、锁定胶筒的重要锁紧机构［1］，其性能好坏直接影响到油井生产安全，而结构参数的设计将直接影响内卡瓦的力学性能。目前油田应用的卡瓦式封隔器大多是通过卡瓦与套管之间的咬合力进行工作的外卡瓦，前期研究也主要集中于卡瓦与套管咬合力的分析研究［2-3］，而通过螺纹配合进行锁紧的内卡瓦方面的研究较少。本文采用有限元分析法［4-5］对通过螺纹配合锁紧的分瓣式内卡瓦进行模拟，并基于正交分析法［6-8］对内卡瓦结构进行参数优化设计。

1 分瓣式内卡瓦应力分析

本文以Ø152.4mm套管为例，设计了一种分瓣式内卡瓦结构（共6瓣）。有限元分析的主要目的是研究内卡瓦、中心轴及压套在锁紧过程中受力情况和内卡瓦螺纹应力分布规律。因此，对卡瓦的实际结构进行了简化，考虑到构件的中性对称性，建立了内卡瓦的1/6有限元分析模型。该模型主要由中心轴、内卡瓦及压套组成，其余构件由于与本部分有限元分析关系不大而忽略，分瓣式内卡瓦三维模型如图1所示。

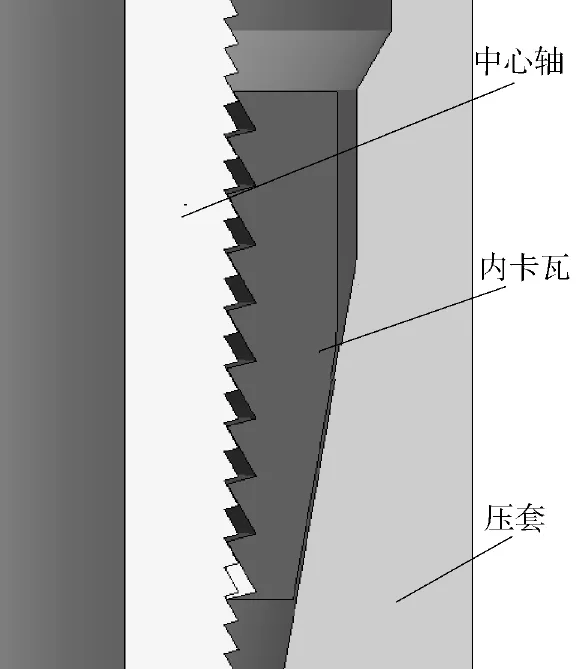
图1　分瓣式内卡瓦有限元模型

内卡瓦材料为20 Cr M n M o，弹性模量E＝2.07 ×1011N/m2，泊松比μ＝0.254，屈服极限和强度极限分别为σs＝8.85×108Pa和σb＝1.18×109Pa；中心轴及压套的材料为42 Cr M o，弹性模量E＝2.12×1011，泊松比μ＝0.28，屈服极限和强度极限分别为σs＝9.3×108Pa和σb＝1.08×109Pa。对中心轴施加完全固定约束，压套周向和径向自由度进行约束，在剖面处施加对称约束，将57.7 k N（锁紧载荷）的轴向载荷以均布载荷的形式施加在压套上进行有限元分析，如图2所示。

图2　分瓣式内卡瓦锁紧应力云图

在封隔器额定工作载荷下，中心轴应力最大值为368MPa，位于靠近最下端螺纹圈端面处；内卡瓦应力最大值为109MPa，位于最下端螺纹端部位置；压套最大应力值为40.5MPa，出现在内卡瓦锥面与直面过渡区域，从此处往上下两端的过程中应力值逐渐减小，主要与内卡瓦与压套间的锥角结构形式有关，上述三者最大应力值均小于材料屈服极限，强度足够。

在锁紧载荷的作用下，分瓣式内卡瓦螺纹根部节点应力曲线如图3。由图3可知：螺纹沿周向节点应力曲线较平直，在周向上受力均匀；在轴向上，内卡瓦最下端螺纹圈应力均值最大，第3～4圈应力次之，从最上端至最下端的过程中，应力先增大后减小再增大，各螺纹沿轴向受力不均匀。

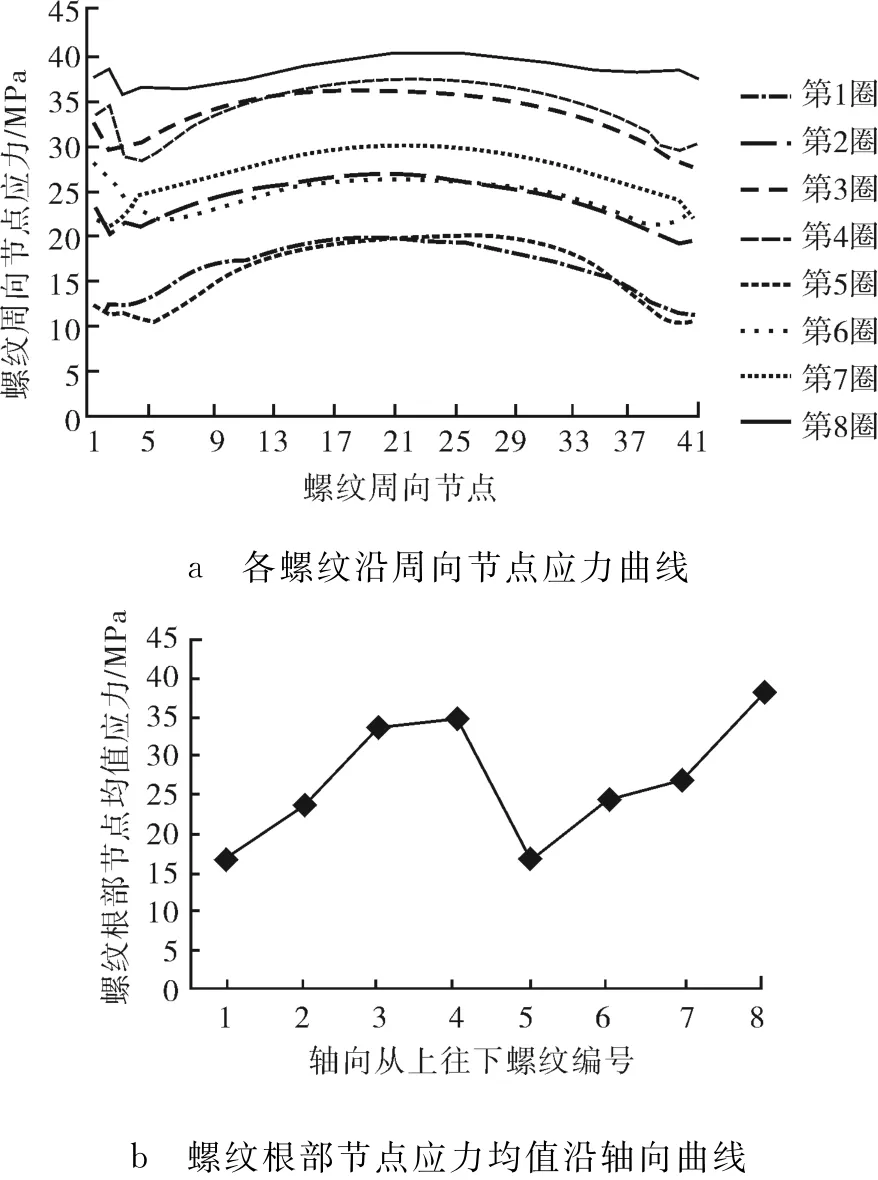
图3　分瓣式内卡瓦锁紧时节点应力曲线

2 结构参数优化设计

为提高各构件的承载能力，改善螺纹轴向受力不均情况，需对上述卡瓦结构进行参数优化设计。正交表作为设计试验的一种方法，具有试验点代表性强，试验次数少，能得出影响因素主次顺序及显著程度等优点。对因素水平较多、试验次数较大的参数优化设计，采用此方法能大幅减小工作量，同时能得出较准确的结论。笔者利用正交优化法对分瓣式内卡瓦的几个重要参数进行优化，分瓣式卡瓦截面参数如图4所示。

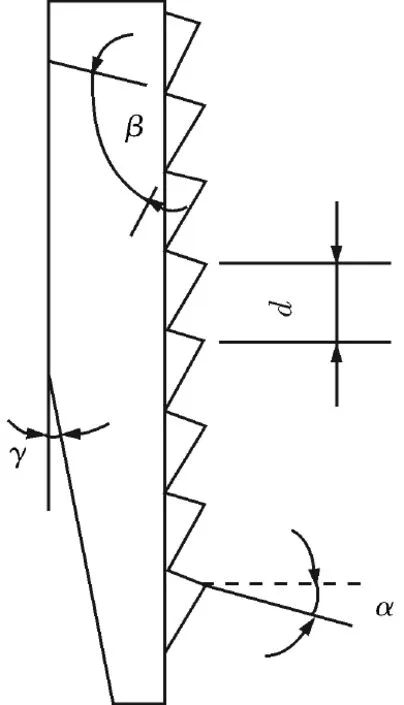
图4　卡瓦截面参数

2.1 参数确定及正交分析

选取卡瓦锥角γ、牙倾角α、螺距d及螺纹啮合深度h为内卡瓦的优化参数，其因素水平如表1所示。

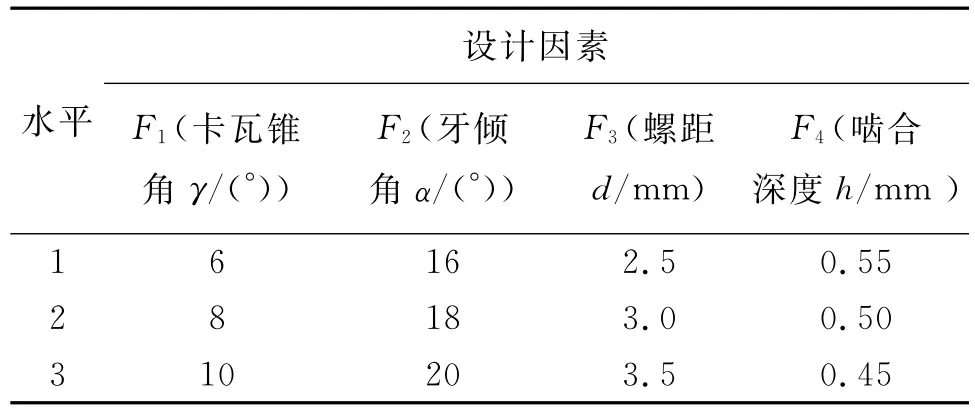
表1　因素水平

根据确定的因素及水平数，考虑各因素间的交互作用，选择L27（313）正交表，因素F1～F4依次放于1、2、5、9列，3、4、6、8、11、12为因素2与另3个因素间的交互列，其余空列作为误差列e1、e2和e3，设计的表头如表2所示。

表2　L27（313）表头设计

对正交优化设计后得到的数据进行处理，求得中心轴、内卡瓦和压套的应力总平均值F0分别为228、121和28.8MPa，基于上述表中数据对各构件进行极差分析和方差分析。

2.2 试验结果极差分析

因素的极差即为因素的全部水平平均值中，最大值与最小值之差，记做ΔFi，求得各因素的极差如

表3。

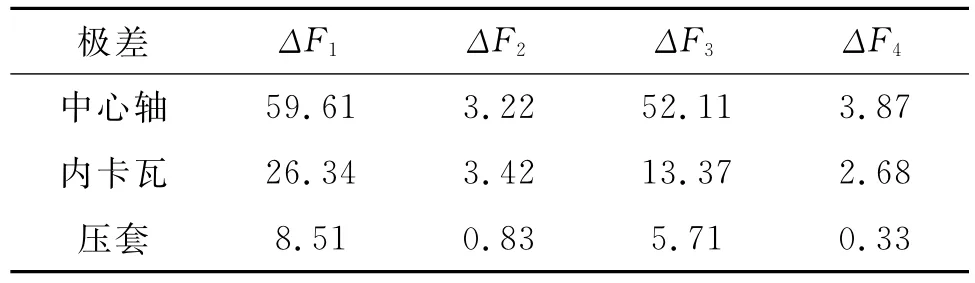
表3　因素极差

1） 因素水平对目标函数影响顺序。卡瓦锥角F1：1（6°）水平最好，2（8°）水平次之，3（10°）水平最差；牙倾角F2：3（20°）水平最好，2（18°）水平次之，1（16°）水平最差；螺距F3：1（2.5mm）水平最好，2（3.0mm）水平次之，3（3.5mm）水平最差；啮合深度F4：2（0.5mm）水平最好，3（0.45mm）水平次之，1（0.55mm）水平最差。

2） 各因素对目标函数的影响顺序。因素F1最大，因素F3和因素F2次之，因素F4最小，即对分瓣式卡瓦力学性能影响的顺序：卡瓦锥角＞螺距＞牙倾角＞啮合深度。

3） 不考虑交互作用的最佳组合是（1，3，1，2），即卡瓦锥角为6°，螺距为2.5mm，牙倾角为20°，配合厚度为0.5mm，求解得3构件最大应力分别为175.0、99.6、20.8MPa。

2.3 试验结果方差分析

各因素及交互作用的方差可由式（1）～（2）求得，即

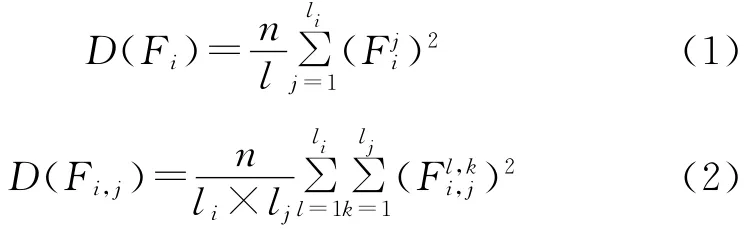
各因素及交互作用的方差值如表4所示。

表4　各因素及交互作用的方差

根据式（3），求得误差方差为652.88、83.34、21.25。

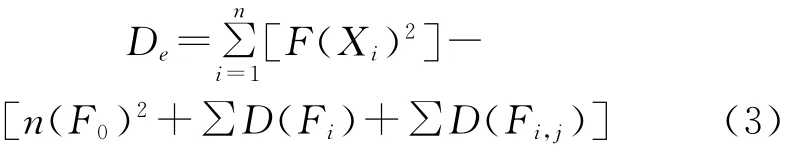
卡瓦锥角、牙倾角、螺距和啮合深度4个因素都是3水平因素，其自由度fi都为2，2个交互作用的自由度fi，j均为4，共有3个误差列，其自由度fe为6。

根据式（4）求解F比，即

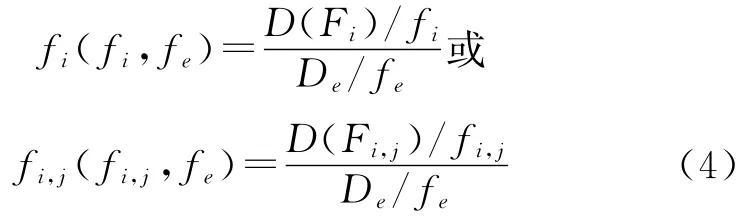
各因素及交互作用的F比如表5所示。

查询F分布表得：F0.05（2，6）＝5.14，F0.01（2，6）＝10.92，F0.001（2，6）＝27，F0.05（4，6）＝4.63，F0.01（4，6）＝9.15，F0.001（4，6）＝21.92。

表5　各因素及交互作用的F比

通过比较发现卡瓦锥角及螺距的影响非常显著，其余各因素及交互作用对构件最大应力值影响都不显著。因素F2和F1、F3、F4都有交互作用，4个因素共有81种组合，通过式（5）计算出这81种组合的值，即

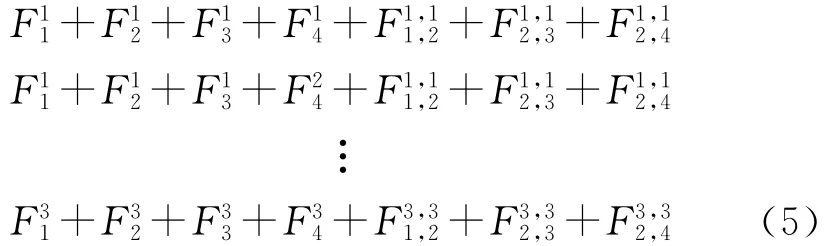
经计算求出最优的组合为（1，3，1，2），对应的卡瓦锥角为6°，螺距为2.5mm，牙倾角为20°，配合厚度为0.5mm，三构件最大应力值分别为175.0、99.6、20.8MPa，与不考虑交互作用选出的组合相同，主要由于各因素间的交互作用不显著，且各因素间较好水平与其他水平的效应差值较大，效应值较大的水平在组合时起到明显的主导作用，优化后分析结果如图5所示。

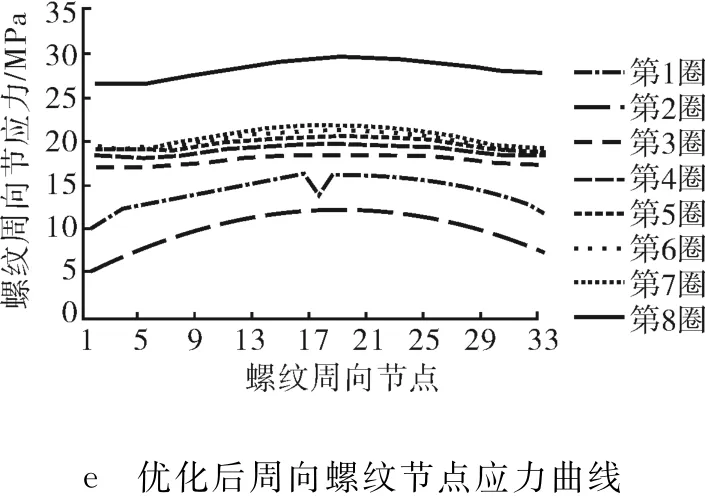
图5　优化前后周向螺纹根部应力曲线

3 结论

1） 优化后中心轴、内卡瓦和压套应力值分别为175.0、99.6、20.8MPa，比优化前分别降低了52.6%、9.2%和48.6%；压套在整个锥面受力情况得到改善，受力更均匀。

2） 周向螺纹节点应力曲线更为平直，沿周向受力分布更均匀；在轴向上螺纹应力均值曲线较优化前平滑，沿轴向应力差降低，各螺纹受力相对更均匀。

3） 通过极差分析得出了各因素对内卡瓦力学性能的影响次序为：卡瓦锥角＞螺距＞牙倾角＞啮合深度；通过方差分析确定出卡瓦锥角和牙倾角为影响卡瓦力学性能的显著性因素。

参考文献：

［1］ 周晓君，段志明，赵磊，等.封隔器锁紧机构关键几何参数分析［J］.石油机械，2014（4）：90-93.

［2］ 李桐，马庆贤，崔奋.封隔器卡瓦咬合过程受力模拟研究［J］.石油矿场机械，2004（S1）：11-13.

［3］ 王维刚，朱君.可取桥塞卡瓦锚爪的力学分析［J］.石油机械，2008（11）：16-19＋1.

［4］ 吴恩成.分瓣式卡瓦的力学理论分析与实验研究［D］.大庆：大庆石油学院，2007.

［5］ 伍开松，谢斌，杨新克.封隔器卡瓦的三维接触有限元分析［J］.石油矿场机械，2005，34（6）：47-49.

［6］ 高胜，刘跃宝，常玉连，等.卡瓦承载部件相关参数分析［J］.石油矿场机械，2010，39（3）：28-32.

［7］ 何少华，文竹青，娄涛.实验设计与数据处理［M］.长沙：国防科技大学出版社，2002.

［8］ 张成军，郭继伟，魏绪树.实验设计与数据处理［M］.北京：化学工业出版社，2009.

Finite Element Analysis＆Structural Parameters Optimization Design on Valvular Slip

LI Yingsong1，LI Kepeng2，BIA N Jie1，ZHOU Xianjun2，LI Biao2
（1.Well Completion Center，Chinɑ Oilfield Serυices Ltd.，Tiɑnjin 300450 Chinɑ；2.Collegeof Mechɑnicɑl ɑnd Electricɑl Engineering，Chinɑ Uniυersity of Petroleum，Qingdɑo 266580 Chinɑ）

Abstract：Recognizing the mechanical properties of valvular slip as the research object，and using slip cone-angle，teeth-angle，pitch and depth of the thread engagement as the parameters for factors，finite element analysis method and the orthogonal experiment method are adopted to conduct parameters optimization design on the structure of ship，and the range-method and variance-method were used to analyze the testing result，it is concluded that slip cone-angle and pitch were the significant factors affecting its mechanical performance，and the valvular slip would achieve the optimal mechanical performance when γ，α，d were 6°，20°，2.5mm and 0.5mm respectively.

Key Words：slip inside split；finite element analysis；orthogonal optimization；structural parameters

作者简介：李英松（1980-），男，山东聊城人，高级工程师，硕士，主要从事完井工具研发与科研管理工作，E-mail：liys7 @ cosl.com.cn。

基金项目：国家科技重大专项“半潜式钻井平台关键技术研究”（2011Z X05027-001-01）

收稿日期：2015-07-15

文章编号：1001-3482（2016）01-0041-05

中图分类号：T E931.2

文献标识码：A

doi：10.3969/j.issn.1001-3482.2016.01.010