桁架结构的倒变量响应面法研究

纪祥飞， 郭　明

(1.山东理工大学 交通与车辆工程学院， 山东 淄博 255049;

2.山东玲珑轮胎股份有限公司， 山东 烟台 264000)



桁架结构的倒变量响应面法研究

纪祥飞1， 郭明2

(1.山东理工大学 交通与车辆工程学院， 山东 淄博 255049;

2.山东玲珑轮胎股份有限公司， 山东 烟台 264000)

摘要：介绍了响应面的基本思想，指出了多项式基响应面在拟合精度方面存在的问题.通过分析多项式形式的响应面方程在设计变量的形式上与结构的位移解析解之间的区别，研究了基于倒变量的响应面方法，并结合算例分析验证了该方法建立的静定桁架结构的位移表达式具有很高的精度.分析结果表明，提出的响应面方法能够精确、快速地解决平面和空间桁架位移的显式化问题.

关键词：倒变量； 桁架结构； 响应面

在结构优化设计数学模型中，需要用优化方法进行优化调整的设计参数称为设计变量，性能变量是结构的各种性态变量，如应力、位移等等，约束条件为设计必须满足的限制条件.其中，约束条件是性能变量的函数，也是设计变量的隐函数[1].这一性质是结构优化设计问题区别于一般的数学规划问题的一个重要特点，也由于这一特点，大大增加了结构优化设计问题的求解难度.要解决这一问题，就必须对约束条件进行显式化，最常用的显式化方法为响应面方法(Response Surface Methodology，RSM),它可以避免函数的求导以及积分，大大降低计算的工作量，也能够保证足够的精度.

响应面方法最初由Box和Wilson于1951年提出，其基本思想是通过一系列确定性实验，用多项式函数来近似隐式极限状态函数，最初主要用于化工领域[2]；1995年，Myers和Montgomery 对响应面及其应用进行了全面的阐述，并把响应面方法定义为“一种用于开发、改进、优化的统计和数学方法”[3]；如今，响应面方法广泛用于优化设计中，即通过合理的试验设计方法构建目标函数、约束函数和设计变量之间的近似函数[4].

传统的多项式基响应面是采用最小二乘法建立的逼近函数，拟合的精度偏低.本文结合桁架结构优化设计问题，提出基于倒变量的响应面法，以期有效提高在展开点附近响应面的拟合精度，这对于结构优化设计非常有利.

1传统多项式基响应面法

1.1多项式基响应面算法简介

根据相关理论研究以及工程实践经验可知，常用的多项式基响应面法的形式为[5]：

线性型

(1)

可分离二次型

(2)

完整二次型(含交叉项)

(3)

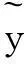
为了推导方便，对式(3)进行统一符号，可得

(4)

(5)

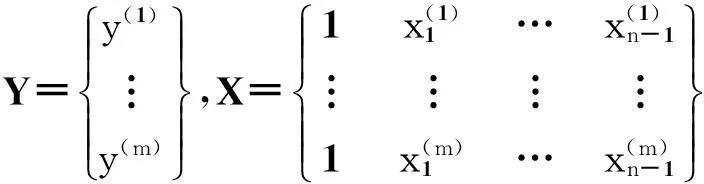
每次试验的表达式可统一写成如下矩阵形式

Y=Xβ+ε

(6)

其中：

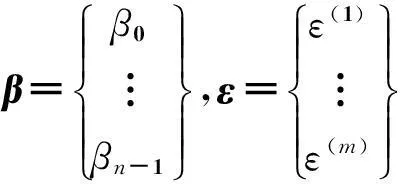
系数向量的无偏估计β可由最小二乘法获得，即令每次试验的误差平方和δ为最小

δ=εTε=(Y-Xβ)T(Y-Xβ)→min

(7)

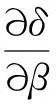
β=(XTX)-1XTY

(8)

1.2多项式基响应面算法的精度分析

在利用多项式基响应面方法进行显式化时，响应面的拟合精度是必须要考虑的，我们用几个简单的算例对多项式基响应面方法的拟合精度进行探讨.本文主要讨论的是桁架结构，选取桁架结构的截面积为设计变量，选取两种截面积变化范围，分别为0.01～0.05m2和0.03～0.04m2，两个范围内试验点个数、分布应相同，且截面均为圆截面，弹性模量E=2.1×1011Pa，泊松比为0.3，以节点的位移为结构的响应.

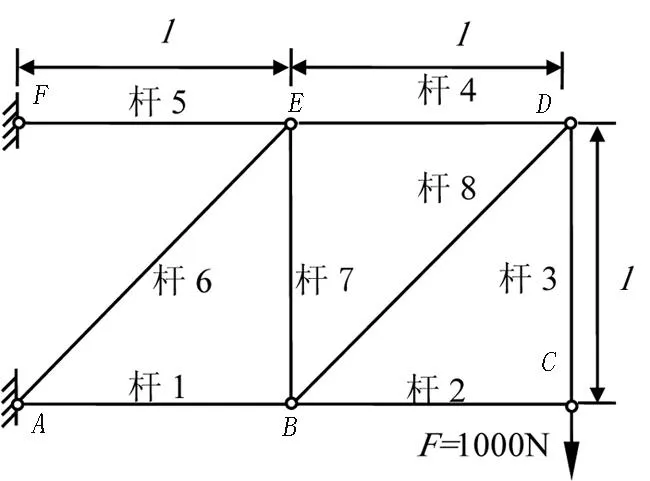
图1　八杆静定桁架结构

利用结构力学中的解析法求得节点C沿力F方向的位移的解析解如下：

(9)

利用多项式基响应面方法求得的八杆桁架的精度以及响应面形式的选择情况见表1.

由表1可以看出：利用多项式基响应面方法对八杆桁架的位移进行显式化求解时，线性型的响应面在检验点处相对误差很高，不能满足求解精度的要求，增加了交叉项对求解的结果影响很小；同时利用传统多项式基响应面方法求得的显式化方程在几何形式上与通过解析法求得的解析解有很大的区别.对比不同检验点取值范围的拟合精度可以发现，3种形式的拟合函数在较小的邻域内的精度要稍好.

表1八杆桁架的拟合精度及响应面形式的选择

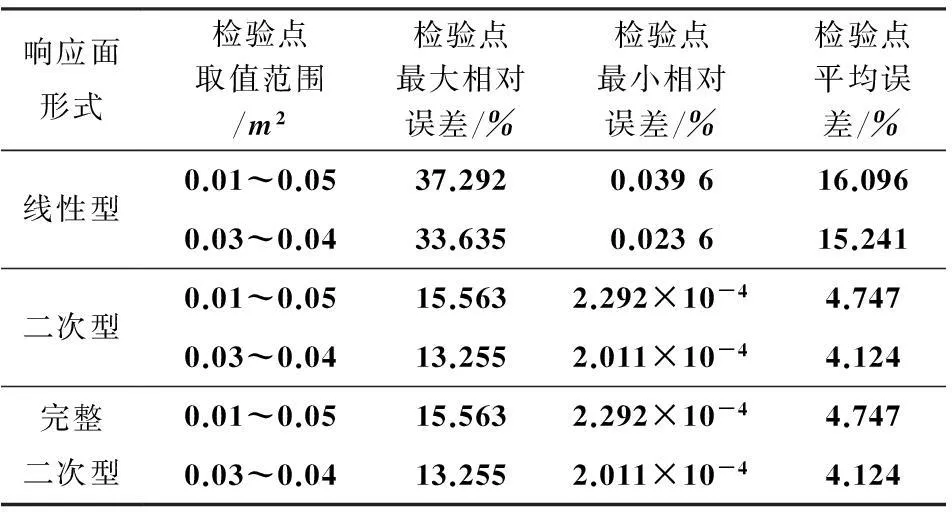
响应面形式检验点取值范围/m2检验点最大相对误差/%检验点最小相对误差/%检验点平均误差/%线性型0.01～0.0537.2920.039616.0960.03～0.0433.6350.023615.241二次型0.01～0.0515.5632.292×10-44.7470.03～0.0413.2552.011×10-44.124完整二次型0.01～0.0515.5632.292×10-44.7470.03～0.0413.2552.011×10-44.124

算例2以一个简单的三杆超静定桁架为例进行分析.三杆桁架的结构以及工况如图2所示.其中工况1：F1=1 000N，F2=0；工况2：F1=0，F2=1 000N，l=1m.由于桁架的结构以及工况均对称，可令A1=A3，同时只考虑第1种工况.

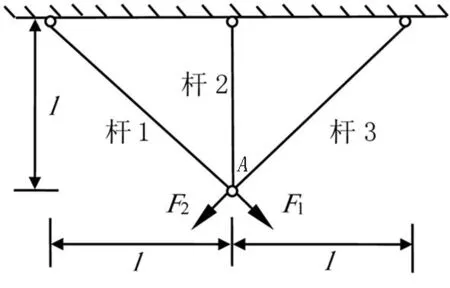
图2　三杆超静定桁架结构

利用结构力学中的知识得到三杆超静定结构的应力为

(10)

(11)

(12)

同时利用卡氏定理求得节点A在力的作用下沿水平方向的位移的解析解为

(13)

利用传统多项式基响应面求解的三杆桁架的精度以及响应面形式的选择情况见表2.

表2三杆桁架的拟合精度及响应面形式的选择

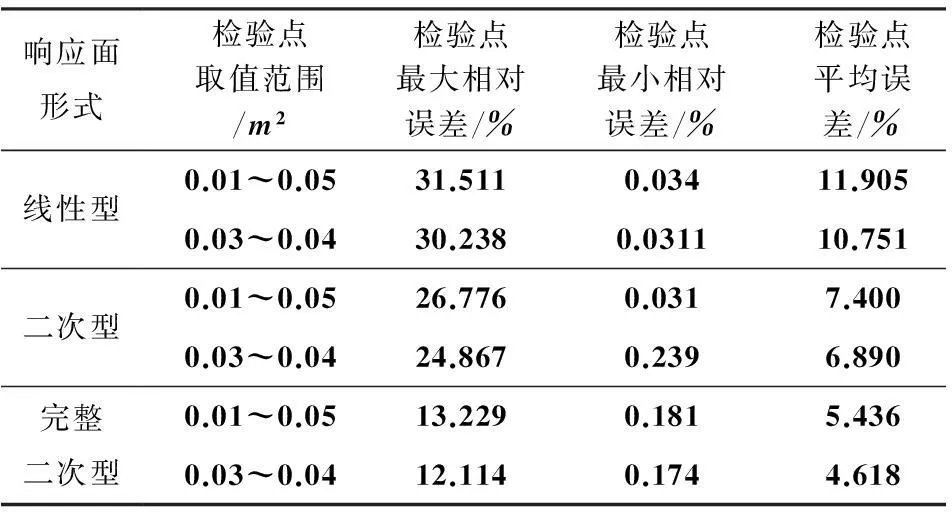
响应面形式检验点取值范围/m2检验点最大相对误差/%检验点最小相对误差/%检验点平均误差/%线性型0.01～0.0531.5110.03411.9050.03～0.0430.2380.031110.751二次型0.01～0.0526.7760.0317.4000.03～0.0424.8670.2396.890完整二次型0.01～0.0513.2290.1815.4360.03～0.0412.1140.1744.618

依据求得的响应面方程及表2中的数据可以看出：利用多项式基响应面方法对三杆桁架的位移进行求解时，和静定结构类似，解析式中设计变量以截面积的倒数形式存在，响应面方程是依据横截面积的直接形式构建的；响应面方程中增加了交叉项能够提高求解的精度，但是提高的效果不明显，同时性能比评价也一般，在检验点处相对误差很高，不能满足拟合精度的要求.另外，同算例1一样，在较小的邻域内，传统多项式基构造的函数拟合精度稍高一些.

2基于倒变量的响应面方法

由材料力学可知，利用莫尔定理求得的桁架结构中某一节点在外力作用下沿某一方向的位移表达式如下：

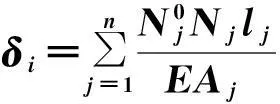
(14)

在静定结构中，若外力已知，则各杆的内力不随设计变量(截面积)的变化而变化，因此节点的位移与倒变量之间是线性关系；在超静定结构中，各杆的内力随着设计变量的变化是相对变化的，但当设计变量增量不大时，可采用静定化假设，即在一轮分析研究中，各杆内力不随设计变量的变化而变化，节点位移与倒变量之间呈线性关系.

基于上述分析，对多项式基响应面做出如下的改进：在利用响应面方法进行桁架结构节点位移的显式化求解时，以倒变量(设计变量的倒数)为基函数进行响应面方程的构建；对于静定结构，只需构建线性型的响应面方程即可获得较高的精度，对于超静定结构，需要构建二次型及完整二次型来保证求解的精度[6].

因此，基于倒变量的多项式基响应面方程的一般形式如下：

(15)

式中：k为设计变量的个数；β0、βi、βii及βij分别为待求解的常数、线性响应的系数、二次响应的系数以及交叉的二次响应的系数.待定系数的求解步骤如下：

(1)通过合理的试验设计方案，选取m(m≥(k+1)(k+2)/2)个试验点，通过试验设计求得各试验点对应的响应值.

(2)可通过式(8)确定由二次多项式表示的响应面函数，此时，式(8)中变量为

待定系数的确定有两种情况：(1)若试验次数为响应面方程求解所需最少的次数，即试验次数为(k+1)(k+2)/2时，可采用直接解线性方程组得到相应的系数；(2)当试验次数大于最少次数即m>(k+1)(k+2)/2时，可以采用式(8)求解待定系数，一般情况下试验次数m都应大于(k+1)(k+2)/2，因为在试验设计合理的情况下，试验点数越多越能体现一般性，这样求解的精度也会更高[7].

由最佳一致逼近原理可知，对已知的数据利用响应面方法进行近似求解时，构建的近似函数在形式上与结构响应的真实解的形式越接近，求解的精度就越高.因此，利用式(15)的形式构建的基于多元有理函数的桁架结构响应面方程，会比利用传统多项式基响应面方程拟合的精度更高，求解的结果更接近于结构的真实响应.

3算例验证

传统多项式基响应面方法，总是直接以设计变量的多项式形式来构建响应面方程，而根据工程经验以及前面的几个算例分析可知，结构优化设计的性能函数中设计变量往往处于分母位置，因此以设计变量的倒数形式作为基函数来构建响应面函数，在形式上能与解析解的形式相统一，求得的显式化方程也更能体现出设计变量与性能函数之间真实的关系.下面利用基于倒变量的响应面方法验证前两个算例的求解精度.

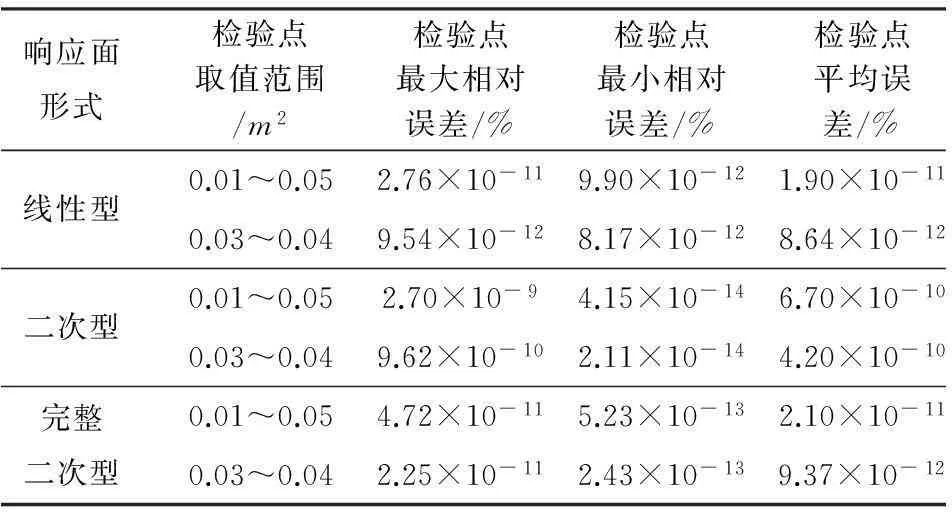
算例3八杆静定桁架结构，利用改进后的响应面方法求得的节点C沿力F方向的位移与真实响应值之间的精度以及响应面形式的选择情况见表3.

表3八杆桁架的拟合精度及响应面形式的选择

响应面形式检验点取值范围/m2检验点最大相对误差/%检验点最小相对误差/%检验点平均误差/%线性型0.01～0.052.76×10-119.90×10-121.90×10-110.03～0.049.54×10-128.17×10-128.64×10-12二次型0.01～0.052.70×10-94.15×10-146.70×10-100.03～0.049.62×10-102.11×10-144.20×10-10完整二次型0.01～0.054.72×10-115.23×10-132.10×10-110.03～0.042.25×10-112.43×10-139.37×10-12

由表3可以看出，利用改进后的基于倒变量的响应面方法进行静定结构的显式化求解时，在不同检验点的取值范围内，求解的精度都很高，相对误差可以控制在1.0×10-8%之内，可认为求解结果是非常准确的，求解的精度比利用传统多项式基响应面方法求解的精度有了明显的提高，证明了改进后的基于倒变量的响应面算法在静定结构显式化求解中的适用性.

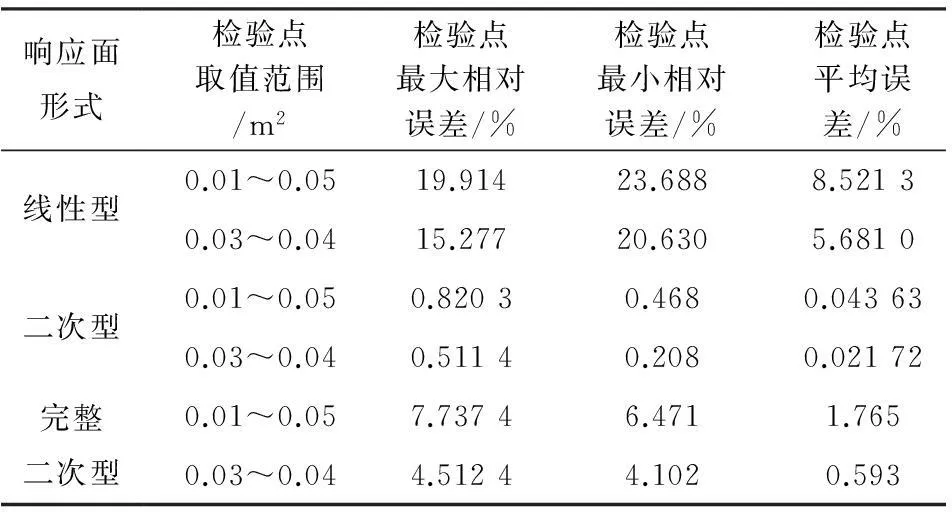
算例4三杆超静定桁架结构，利用改进后的响应面方法得的节点A沿力F方向的位移与真实响应值之间的精度以及响应面形式的选择情况见表4.

表4三杆桁架的拟合精度及响应面形式的选择

响应面形式检验点取值范围/m2检验点最大相对误差/%检验点最小相对误差/%检验点平均误差/%线性型0.01～0.0519.91423.6888.52130.03～0.0415.27720.6305.6810二次型0.01～0.050.82030.4680.043630.03～0.040.51140.2080.02172完整二次型0.01～0.057.73746.4711.7650.03～0.044.51244.1020.593

由表4可以看出：利用改进后的响应面方法求解超静定结构的位移时，检验点处的求解精度与利用传统多项式基响应面求解的结果相比都有了明显的改善，尤其是含交叉项的完整二次型，精度提高的最明显，通过缩小检验点的取值范围，同样精度也得到了明显的提高，且求解的精度基本能够满足工程实际的需要.

4结论

(1)利用基于倒变量的多项式基响应面方法求解静定结构的显式化时，求解的精度极高，检验点处的相对误差可以严格控制在万分之一以内，这主要是因为本文构建的响应面方程与结构的解析解在形式上保持了高度的一致，因此可以认为构建的响应面方程可以全面地反映性能函数和设计变量之间的显式关系.

(2)超静定结构的求解精度比静定结构的差了一些，这主要是由于在构建响应面方程时，为了与静定结构的形式相统一，采用了静定化假设，在实际求解过程中，各杆内力的变化是伴随着设计变量的变化而变化的，但是通过缩小检验点的取值范围，求解精度得到了明显的提高，且完整二次型的精度完全能够满足工程实际的需要，证明了基于倒变量的多项式基响应面方法可以有效地解决结构优化设计中隐函数的显式化问题，且在较大的求解区域内，精度都能够得到保障.

参考文献:

[1] 孙焕纯,柴山,王跃方,等. 离散变量结构优化设计[M]. 大连:大连理工大学出版社,2001.

[2] 赵维涛, 邱志平. 基于合理子域的改进响应面方法[J]. 力学学报, 2014,46 (3):409-416.

[3]吕辉,于德介,谢展，等. 基于响应面法的汽车盘式制动器稳定性优化设计[J]. 机械工程学报,2013,49(9):55-60.

[4]吕大刚, 贾明明, 李刚. 结构可靠度分析的均匀设计响应面法[J]. 工程力学,2011,28(7):109-116.

[5]隋允康,宇慧平. 响应面方法的改进及其对工程优化的应用[M]. 北京:科学出版社,2011.

[6]赵维涛, 邱志平. 基于切平面布点的一种改进响应面方法[J]. 工程力学, 2014,31 (10):21-26.

[7]路怀华,于德介,吕辉. 基于响应面法的汽车转向系统可靠性优化[J]. 汽车工程, 2015,37(1):102-106.

(编辑：郝秀清)

The research of reciprocal variable of truss structure′s response surface method

JI Xiang-fei1, GUO Ming2

(1.School of Transportation and Vehicle Engineering, Shandong University of Technology, Zibo 255049, China;2.Shandong Linglong Tire Company Limited, Yantai 264000, China)

Abstract:The basic idea of response surface is introduced, and the problems of the polynomial-based response surface in fitting accuracy are also pointed out. Through the literature query and the analysis of the difference between design variables form of the polynomial response surface and the analytical solution of structure displacement, the response surface method based on reciprocal variable is proposed and studied, the high precision of static structure displacement expression was verified by example. The results showed that the proposed response surface method can accurately and quickly solve the plane and space truss displacement explicit issues.

Key words:reciprocal variable; truss structure; response surface

中图分类号：U467.1

文献标志码：A

文章编号：1672-6197(2016)02-0027-04

作者简介：纪祥飞，男，15275995247@139.com; 通信作者： 郭明，男，guoming04073215@126.com.

收稿日期：2015-03-16