道路组合线形对交通安全的仿真分析

秦国茂，宇仁德，于晓龙

(山东理工大学 交通与车辆工程学院，山东 淄博 255049)



道路组合线形对交通安全的仿真分析

秦国茂，宇仁德，于晓龙

(山东理工大学 交通与车辆工程学院，山东 淄博 255049)

摘要：为了让车辆能够以安全速度通过弯坡组合线形路段，在仿真软件ADAMS/Car中建立车辆模型、道路模型以及车路耦合模型，分别对选取的半径、超高和坡度与安全速度阈值之间的关系进行研究，并通过正交分析的方法，结合选取的不同水平因素组合的仿真结果，建立道路线形参数与安全速度的统计模型.仿真的结果表明：弯道半径、超高与安全速度阈值之间呈正幂函数关系，坡度与安全速度阈值之间呈负幂函数关系，安全速度阈值与半径、超高以及坡度的统计模型为三元非线性.

关键词：组合线形；安全速度阈值；ADAMS/Car仿真；统计模型

组合线形是道路受地形、地貌以及环境保护所限，由下坡路段和圆曲线弯道组成的复杂路段.车辆在该路段行驶时不仅受到重力影响，同时还受到离心力的影响.而在离心力的作用下，车辆可能会出现侧滑和侧翻的事故，近几年弯坡组合线形路段的亿车公里事故为89.06，远远大于其他路段，严重威胁着人们的生命和财产安全.

国内外的学者对组合线形的几何参数与行车安全的关系做了很多研究[1-5]，但主要从事故率和车辆的制动性能的角度来评价线形参数的合理性与协调性[6-11].本文基于虚拟道路行驶仿真技术，得到了不同几何参数弯坡道路模型下的车辆轮胎受力曲线，确定车辆安全通过的速度阈值，并分析线形参数与安全速度阈值的关系，建立安全速度阈值的统计模型.本文的研究方法可以在已知组合线形参数的情况下推断出标准车型能够安全通过的速度，为组合线形行车安全的研究提供了一个新的途径.

1问题的提出及仿真思路

组合线形由于其特殊性，往往成为交通事故的高发地段，因此研究车辆在该路段安全速度阈值与线形指标间的关系是当前亟待解决的问题之一.

解决该问题首先要明确在道路几何线形中影响安全速度阈值的主要因素，在平面圆曲线中半径和设计速度有如下关系：

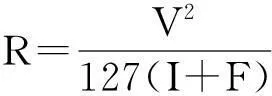
(1)

式中：R为圆曲线半径；V为设计速度；I为超高；F为横向摩擦系数.

在公式(1)中由于横向摩擦系数F通常取固定值，所以影响安全速度的几何因素为平曲面的半径R和超高I、纵断面中的坡度P.针对半径、超高和坡度与安全速度阈值的关系通过多体动力学仿真软件ADAMS/Car分别建立车辆模型、道路模型和车路耦合模型进行仿真研究.

本次仿真试验的思路是首先分别单独研究半径、超高、坡度和安全速度阈值之间的回归模型，然后通过正交试验的方法建立三因素五水平正交表，根据正交表水平组合进行仿真试验，得出在不同水平组合下的安全速度阈值，最后将正交表中数据通过数据分析软件spss求得回归模型的参数，得到组合线形下的安全速度阈值预测模型.本次仿真试验中的各影响因素水平见表1.

表1影响因素水平

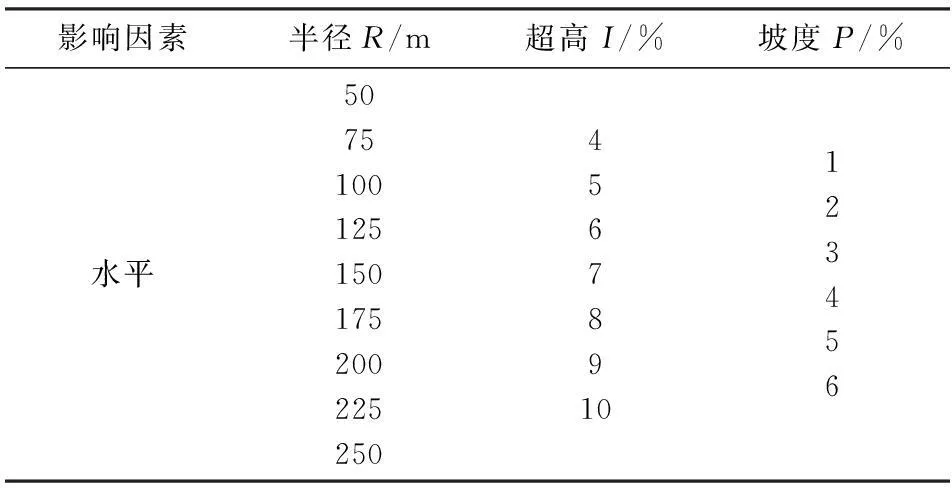
影响因素半径R/m超高I/%坡度P/%水平507510012515017520022525045678910123456

2车辆和道路模型的建立

2.1车辆模型的建立

选用ADAMS/Car中的MDI_Demo_vehicle.asy装配为车辆模型，在该模型中悬架为双横臂独立悬架，转向系统为齿条齿轮转向系统，轮胎采用对实验数据有更高精度的魔术公式Magic-Formula模型，车辆参数见表2.

2.2道路模型的建立

本文建立的是包含平曲面和纵曲面在内的组合线形，3D道路模型，路面的左右侧摩擦系数均为0.7，建立该模型需要ADAMS/Car的路面建模器Road Builder来实现，完成的道路模型如图1所示.

表2车辆参数

质量/kg轴距/m前轮轮距/m后轮轮距/m1527.72.561.521.6

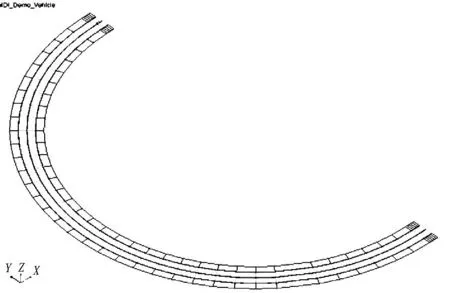
图1　弯道模型

3仿真结果分析

3.1平面弯道半径对安全速度阈值影响的仿真

通过道路建模器分别建立半径为50m、75m、100m、125m、150m、175m、200m、225m、250m的无超高平曲面.通过逐渐增大车辆的行驶速度，并观察车辆后轮所受侧向力变化来判断车辆是否发生侧滑，进而得到车辆的安全速度阈值，仿真结果如图2～图10所示.

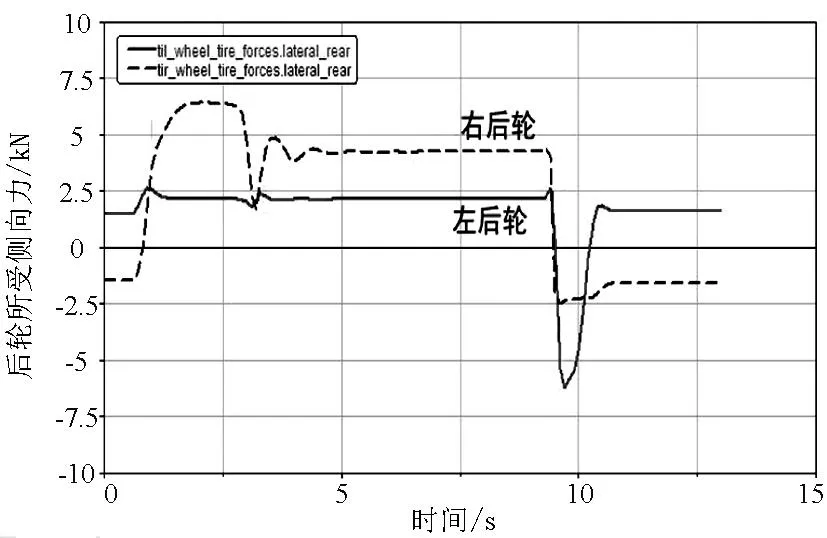
图2　R=50m、V=83km/h时后轮所受侧向力

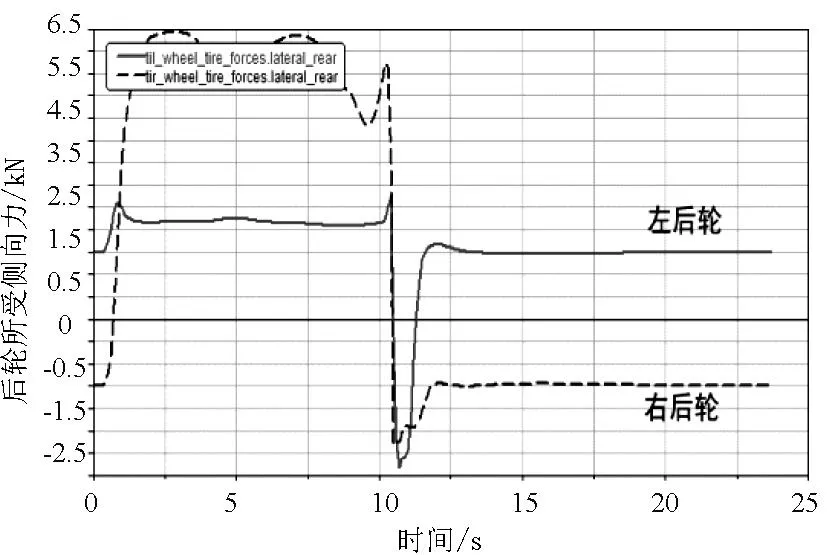
图3　R=75m、V=98km/h时后轮所受侧向力

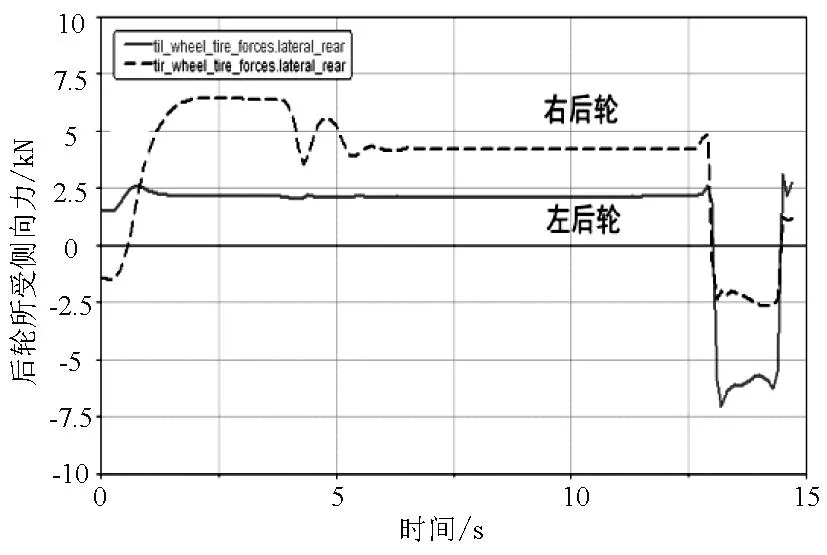
图4　R=100m、V=113km/h时后轮所受侧向力

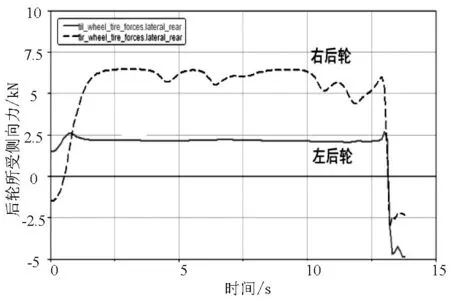
图5　R=125m、V=126km/h时后轮所受侧向力

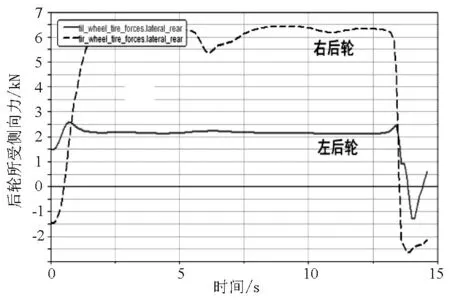
图6　R=150m、V=137km/h时后轮所受侧向力

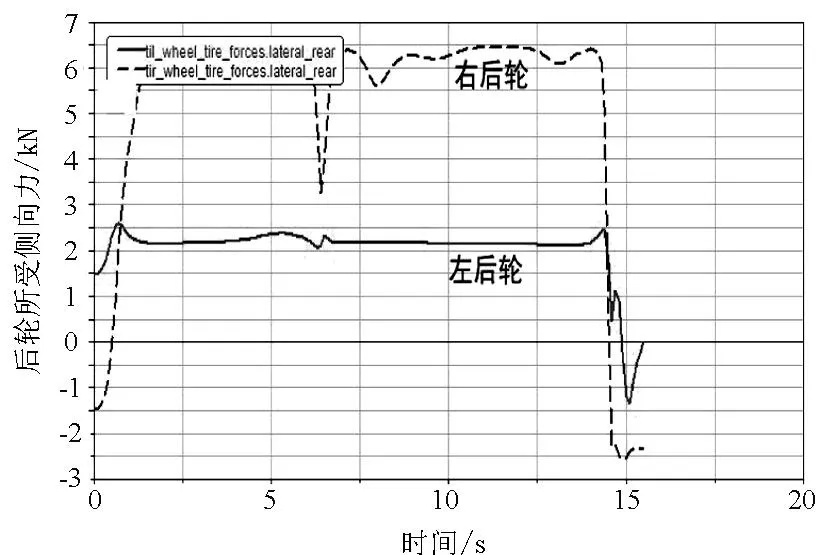
图7　R=175m、V=148km/h时后轮所受侧向力

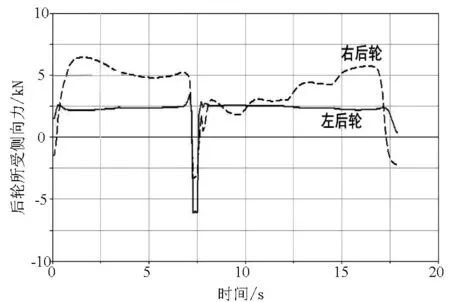
图8　R=200m、V=156km/h时后轮所受侧向力

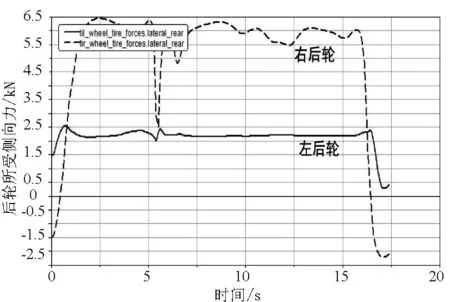
图9　R=225m、V=164km/h时后轮所受侧向力

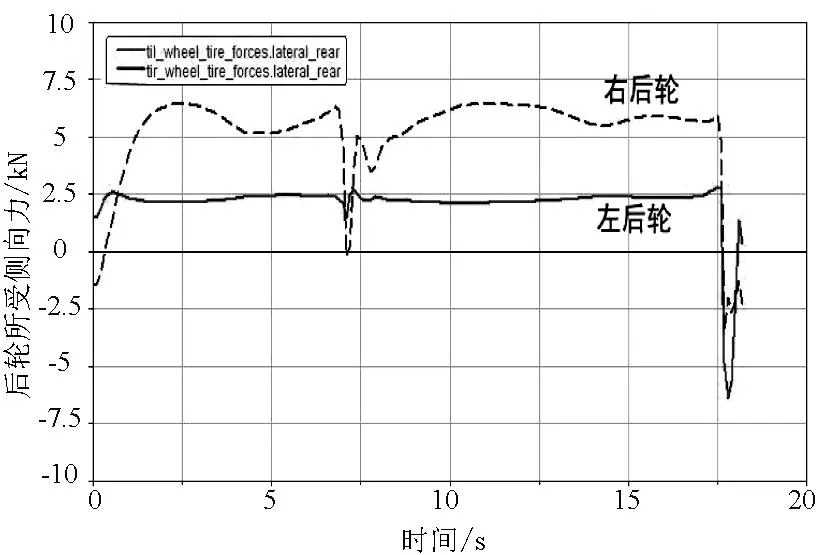
图10　R=250m、V=173km/h时后轮所受侧向力

3.2平面弯道超高对安全速度影响的仿真

仿真试验使用半径为100m、超高值范围为4%～10%的平曲面弯道对超高与安全速度的阈值的关系进行仿真，当速度达到安全阈值时后轮侧向力如图11～图17.

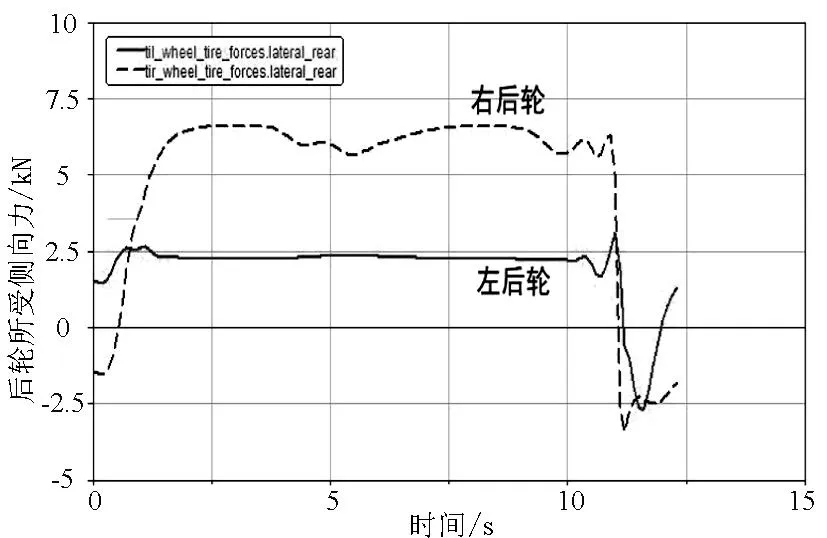
图11 　I=4%、V=116km/h时后轮所受侧向力

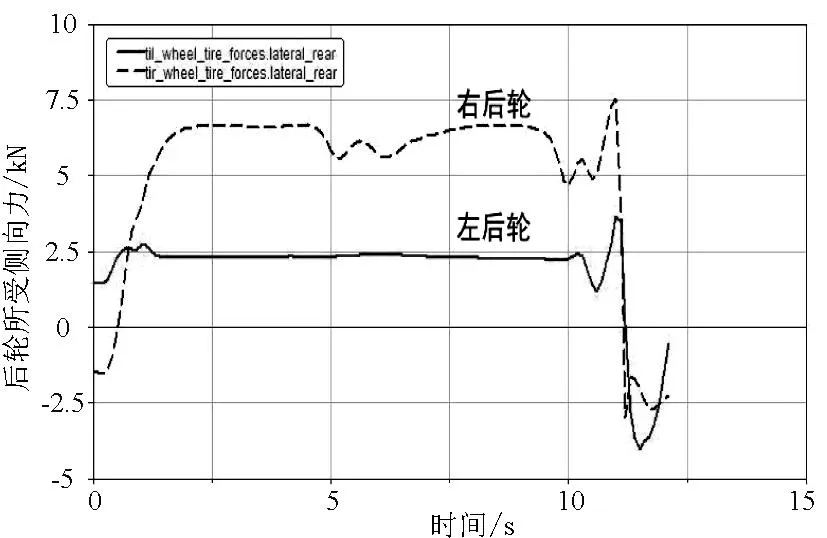
图12　I=5%、V=117km/h时后轮所受侧向力

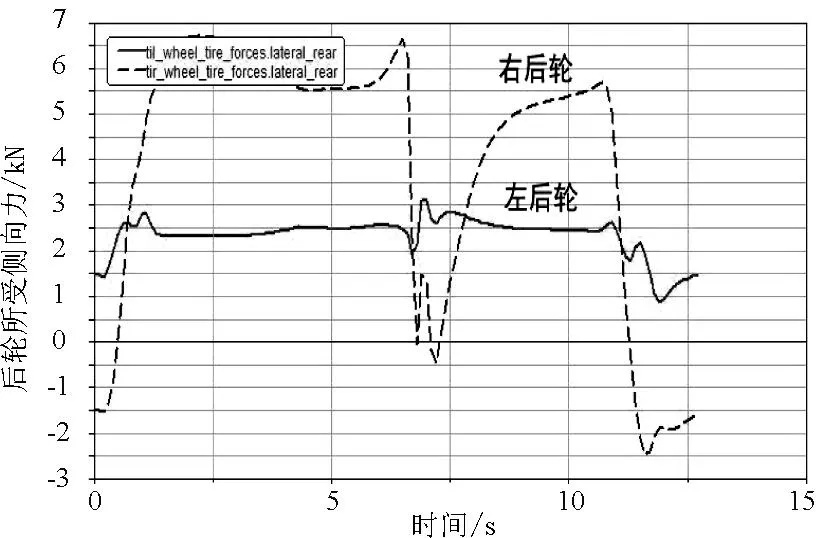
图13　I=6%、V=119km/h时后轮所受侧向力

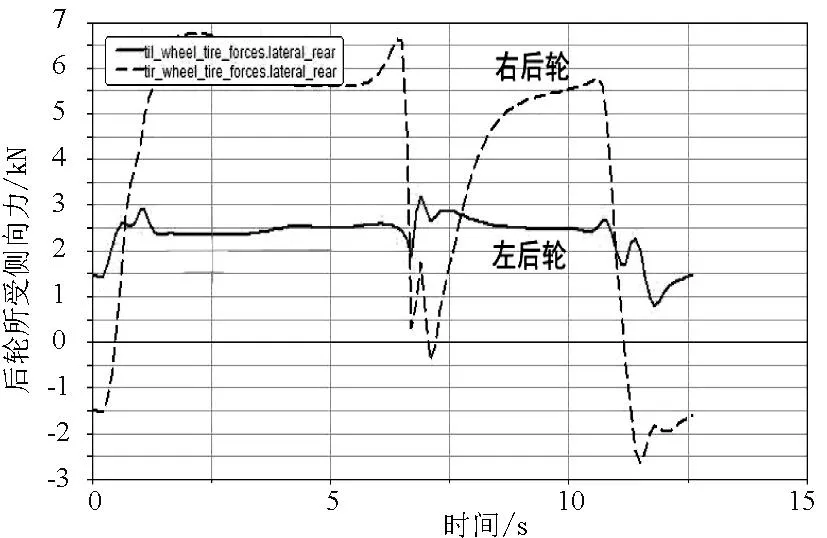
图14　I=7%、V=122km/h时后轮所受侧向力

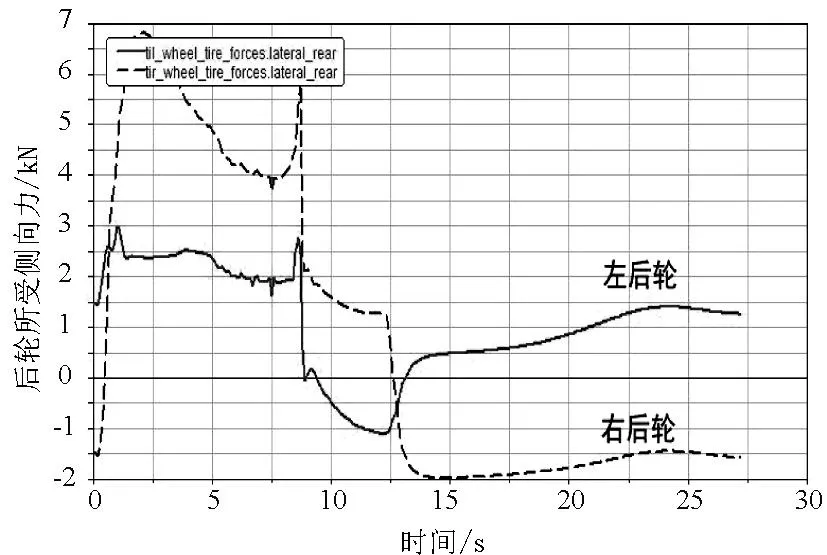
图15　I=8%、V=125km/h时后轮所受侧向力

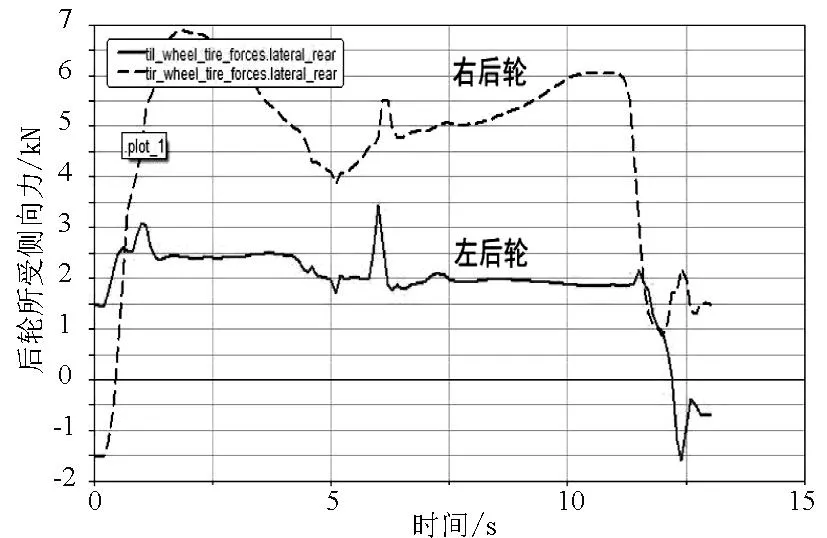
图16　I=9%、V=127km/h时后轮所受侧向力

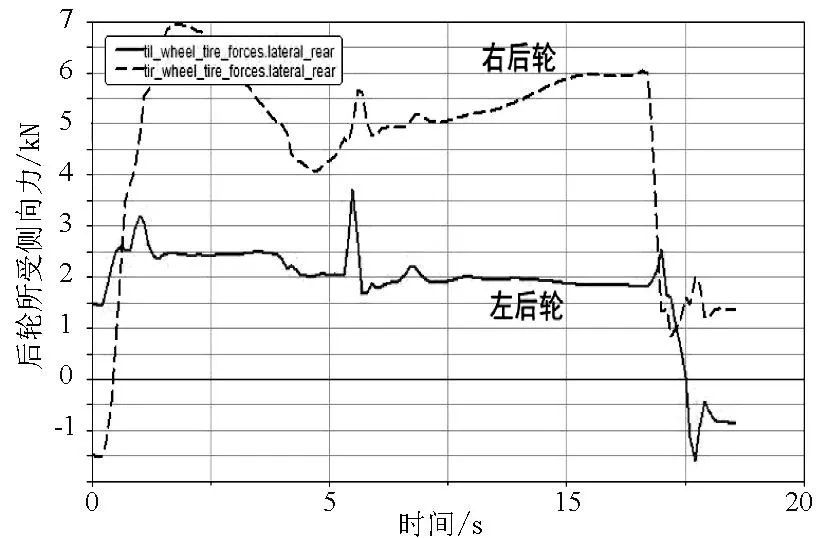
图17　I=10%、V=129km/h时后轮所受侧向力

3.3纵断面坡度对安全速度影响的仿真

仿真试验使用半径为200m、坡度值范围0.01～0.06的组合线形弯道对坡度与安全速度的阈值的关系进行仿真，当速度达到安全阈值时后轮侧向力见图18～图23 。

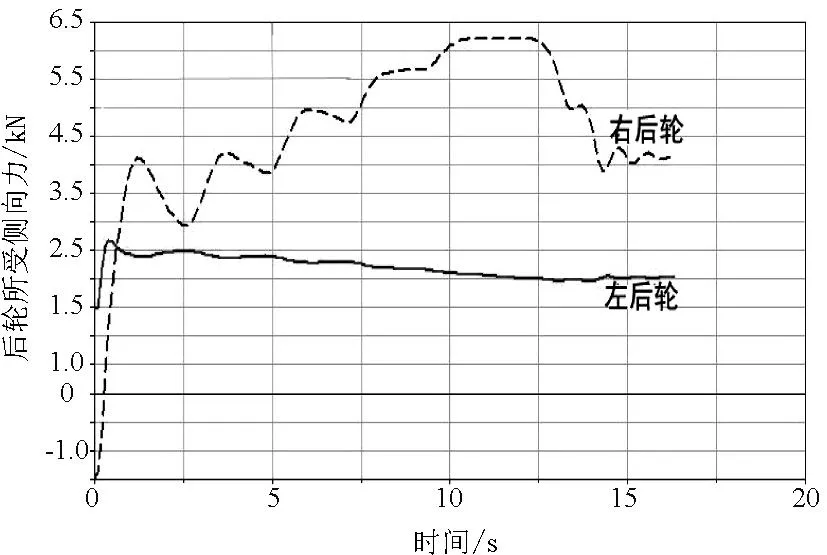
图18　P=0.01、V=125km/h时后轮所受侧向力

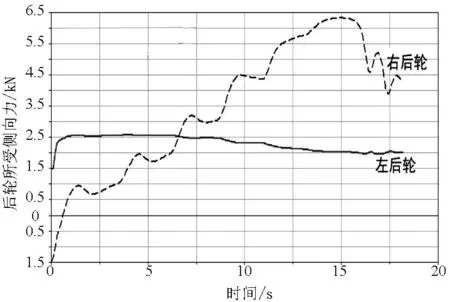
图19　P=0.02、V=105km/h时后轮所受侧向力

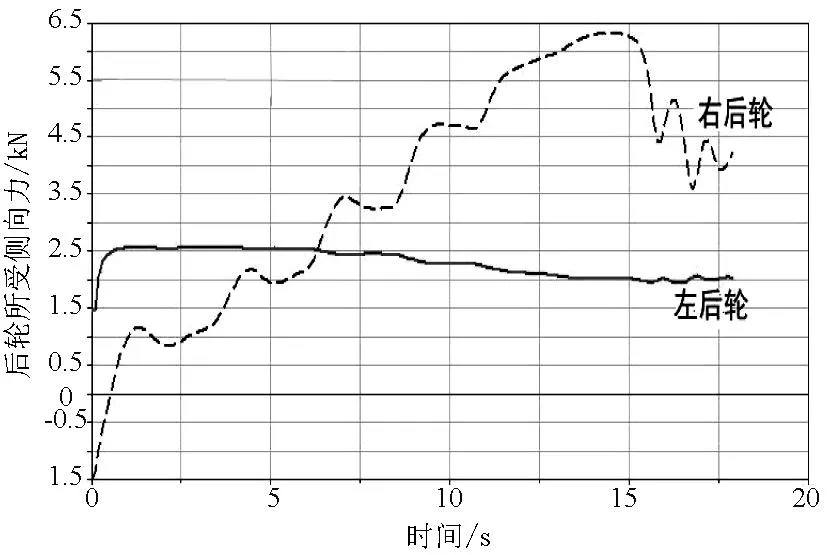
图20　P=0.03、V=95km/h时后轮所受侧向力

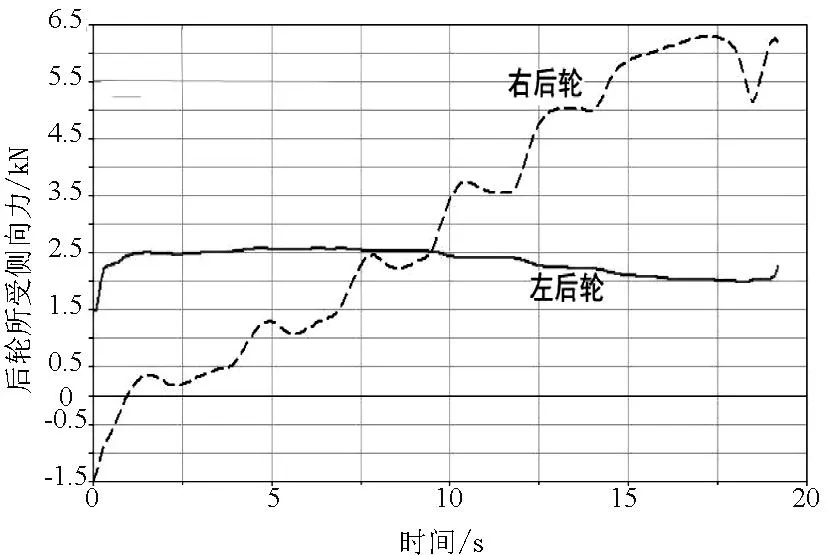
图21　P=0.04、V=86km/h时后轮所受侧向力

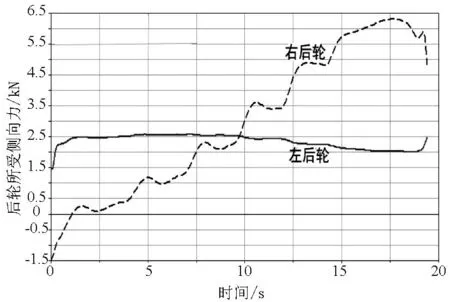
图22　P=0.05、V=78km/h时后轮所受侧向力

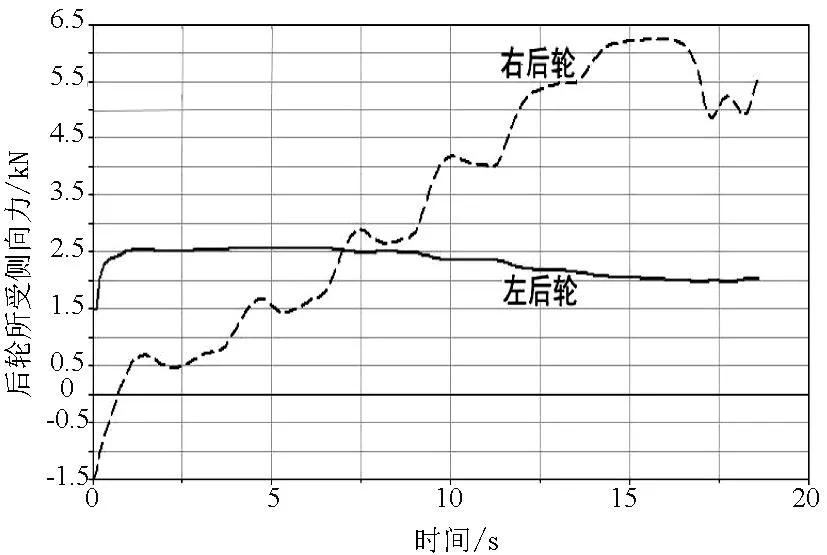
图23　P=0.06、V=73km/h时后轮所受侧向力

3.4仿真结果分析

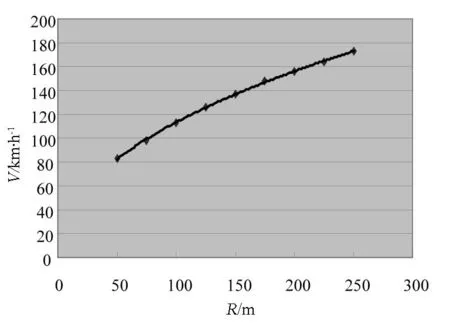
图24　半径与安全速度阈值关系

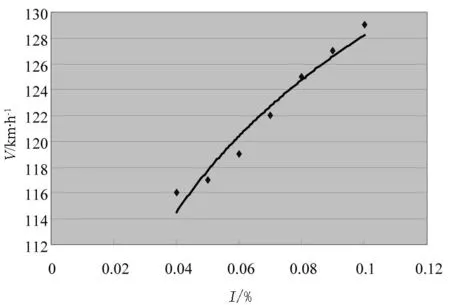
图25　超高与安全速度阈值关系

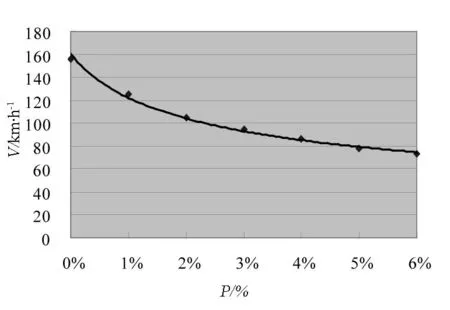
图26　坡度与安全速度阈值关系

仿真实验发现，弯道半径、超高逐渐增加的同时，车辆的安全速度阈值也在逐渐增加；纵断面坡度逐渐增加的同时，安全速度的阈值逐渐降低.当车速达到安全阈值时，车辆发生侧滑导致后轮所受侧向力急剧变化并且无法恢复到初始状态，它们之间的对应关系如图24～图26所示.可以看出R-V、i-V的关系近似正幂函数变化，而p-V的关系近似负幂函数变化。综合分析可知四者之间的关系为三元非线性.为了易于转化为线形回归分析并尽量符合客观实际，假设关系模型为

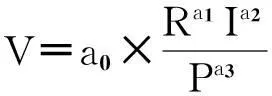
(2)

式中：V为车辆安全通过的速度阈值；R为圆曲线弯道半径；I为超高；a0、a1、a2、a3为待定参数。

将模型(2)等号两边取对数，得

lnV=lna0+a1lnR+a2lnI-a3lnP

(3)

令lnV=V′，A0=lna0，R′=lnR，I′=lnI，P′=lnP代入式(3)中得

V′=A0+a1R′+a2I′-a3P′

(4)

式(4)是一个三元线形方程，本文利用正交分析的方法来求得参数A0、a1、a2、a3.

4正交分析试验

本次正交分析试验为三因素五水平，根据正交分析的原则，采用L25(53)正交表，正交设计方案及安全速度阈值见表3，待定参数的计算结果见表4.

由表4可知，四个回归参数的值分别为A0=3.489, a1=0.21,a2=0.059,a3=0.029.把它们代入式(2)中可得

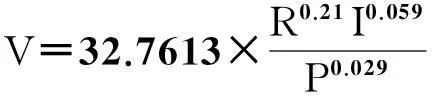
(5)

式中:V为安全速度阈值； R为弯道半径； I为弯道超高； P为纵坡坡度.

为了检验模型的有效性，对式(5)进行F检验.即将安全速度阈值的变差SST分为两个部分：

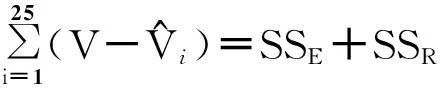
(6)

表3正交设计方案及安全速度阈值

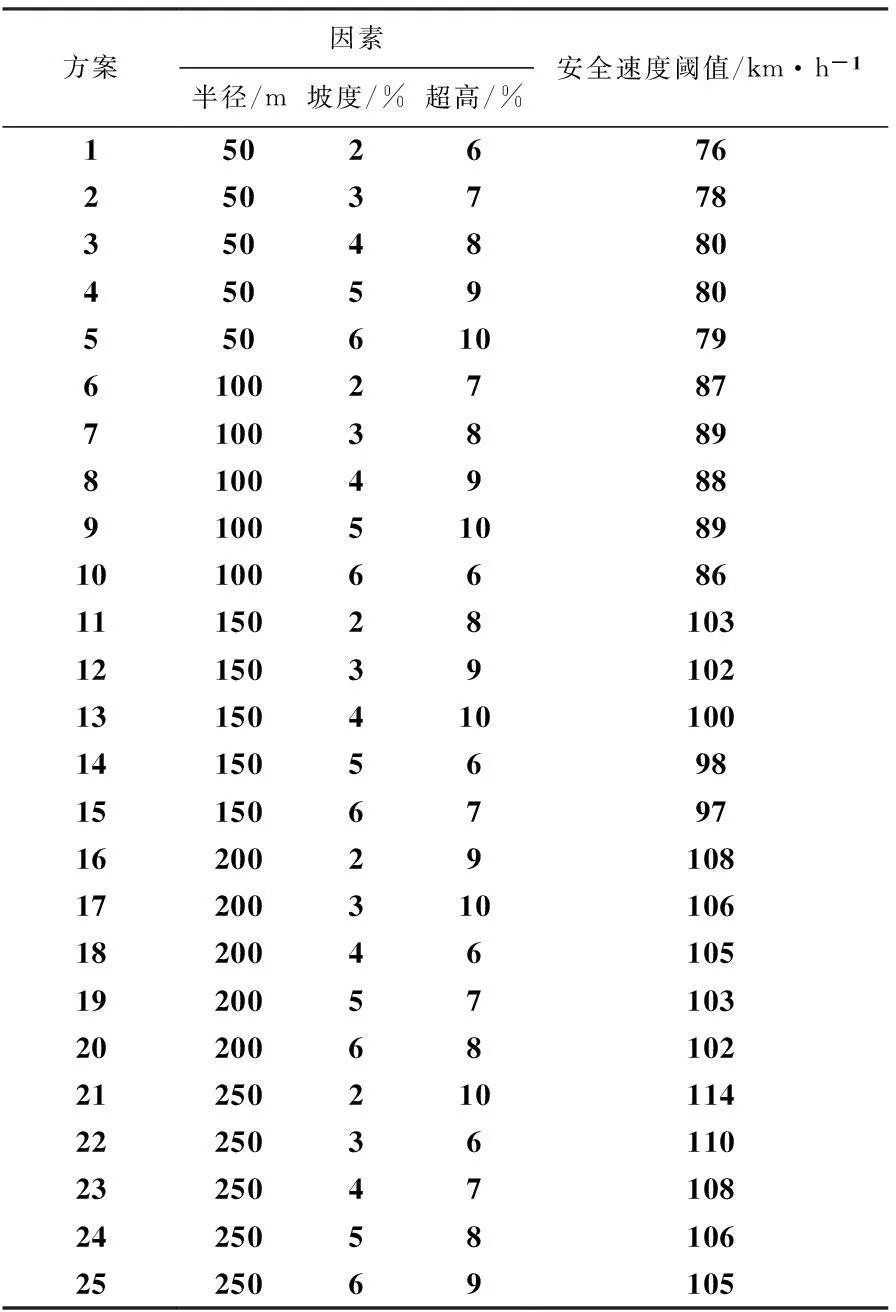
方案因素半径/m坡度/%超高/%安全速度阈值/km·h-11502676250377835048804505980550610796100278771003889810049889100510891010066861115028103121503910213150410100141505698151506797162002910817200310106182004610519200571032020068102212502101142225036110232504710824250581062525069105

表4回归系数分析

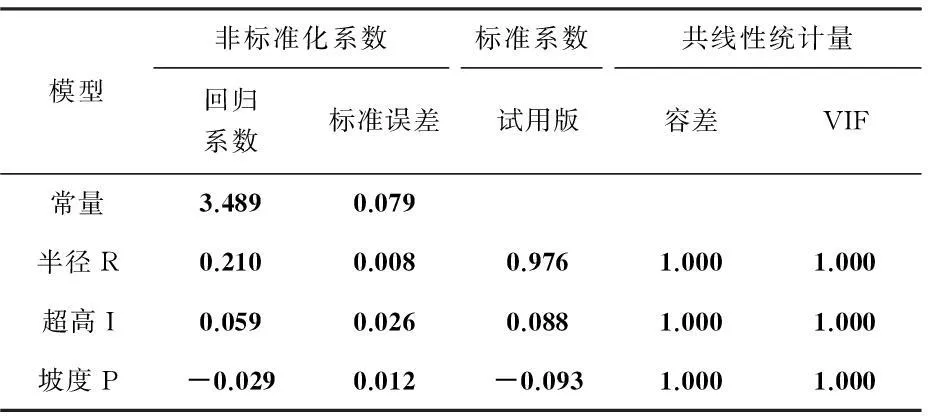
模型非标准化系数标准系数共线性统计量回归系数标准误差试用版容差VIF常量3.4890.079半径R0.2100.0080.9761.0001.000超高I0.0590.0260.0881.0001.000坡度P-0.0290.012-0.0931.0001.000

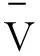
这三个平方和自由度分别为n-1、s、n-s-1，其中n为样本容量，s为待定参数个数.

三个平方和的均方分别为

MST=SST÷(n-1)=129.2363

MSR=SSR÷s=763.4725

MSE=SSE÷(n-s-1)=14.389

所以F=MSR÷MSE=50.06.

在显著性水平为α=0.05、自由度为4、20的条件下可查F分布表F0.05=2.87.可见F=50.06>F0.05=2.87，即95%的把握回归方程(5)是有效的.

5结束语

论文针对国内道路组合线形事故多发的问题，通过ADAMS仿真的方法，对组合线形的主要参数分别取值，并在不同半径、不同超高以及坡度情况下得到最大安全速度，建立了安全速度阈值的预测模型.结果表明：安全速度阈值与线形参数的三元非线性的函数模型是有效的，能够得到组合线形的最大安全速度.

参考文献:

[1] JTG B01-2003，公路工程技术标准[S].

[2] Cheng G Z, Pei Y L. Relationship between speed and traffic-accident and speed limit on free way[J]. Jo-urnal of Harbin Institute of Technology (New Series), 2008,15(2):49-56.

[3] 符锌砂.基于平纵组合线形的理论运行速度预测模型[J].长安大学学报：自然科学版,2010,30(3):24-27.

[4] 郭应时,付锐.山区公路事故率和平面线形的关系[J].交通运输工程学报,2012,12(1):63-70.

[5] 张晓明,孟祥海.山区及平原区高速公路几何线形指标与事故率间关系对比研究[J].公路工程,2014,39(1):212-220.

[6] Leish J E. New concepts in design speed application in transportation research record[J].TRB,1997,16(2):71-78.

[7] 杨少伟.可能速度与交通事故的关系[J].长安大学学报：自然科学版,2009,29(4):34-38.

[8] 景天然.公路线形使用质量评价系统[J].中国公路学报,1991,4(4):29-36.

[9] 裴玉龙,马骥.道路交通事故道路条件成因分析及预防对策研究[J].中国公路学报,2003,16(4):77-82.

[10] 吴峰.山区高速公路圆曲线最小半径确定方法的研究[D].西安：长安大学,2005.

[11] Stijn D,Jan V,An E. Additional road markings as an indication of speed limits: results of a field experiment and a D-riving simulator study[J]．Accident Analysis and Prevention,2010,42(3):953-960.

[12] Kanellaidis G,Golias J,Efs tathi adis S. Drivers speed behaviour on rural road curves[J].Traffic Engineering and Control,1990,31(7):414-415.

(编辑：刘宝江)

Analysis of the simulation of road combination alignment of driving safety

QIN Guo-mao, YU Ren-de, YU Xiao-long

(School of Transportation and Vehicle Engineering, Shandong University of Technology, Zibo 255049,China)

Abstract:We establish vehicle model, road model and vehicle-road coupling model by ADAMS/Car, and then study the relationship among the selected radius, superelevation and gradient with the threshold for the vehicle pass through the combination alignment by safety speed. To build the statistical model amongthe safety velocity's threshold with road linear parameters, on the basis of simulation result of different combination of factors and levels by orthogonal analysis. The simulation results show that they are positive power function relationship between radius and velocity threshold, superelevation and velocity threshold; it is negative power relationship between gradient and velocity threshold; the statistical model amongradius, superelevation, gradient and velocity threshold is three variables nonlinear.

Key words:combination alignment；safety velocity's threshold；ADAMS/Car simulation；statistical model

中图分类号：X913.4

文献标志码：A

文章编号：1672-6197(2016)02-0039-06

作者简介:秦国茂，男, 835356568@qq.com; 通信作者： 宇仁德 ，男，yed65@sina.com

收稿日期：2015-01-05