含时滞反馈控制的1/4车辆模型减振研究

朱　坤，任传波，王　飞，瞿育文

(山东理工大学 交通与车辆工程学院，山东 淄博 255049)



含时滞反馈控制的1/4车辆模型减振研究

朱坤，任传波，王飞，瞿育文

(山东理工大学 交通与车辆工程学院，山东 淄博 255049)

摘要：建立含时滞状态反馈控制的1/4车辆悬架模型，采用稳定性切换方法对车辆悬架系统的稳定性进行分析.在频域内分析系统振动特性，以车身加速度的幅频特性作为目标函数，借助MATLAB优化工具箱，优化出最佳反馈增益系数和时滞.MATLAB/Simulink仿真结果表明，时滞反馈控制能有效提高车辆悬架的减振性能，改善车辆平顺性.

关键词：时滞状态反馈；稳定性切换；幅频特性；MATLAB/Simulink；车辆平顺性

时滞一方面对系统的性能有很大的影响，甚至可能导致系统失稳，另一方面时滞能够改变振动相位，可以利用时滞来控制系统的动力学行为[1].美国学者Olgac[2]最早提出了时滞减振技术，通过引进一个带有时滞状态反馈的动力吸振器来减小主系统振动.赵艳影等[3-4]的研究结果表明，时滞非线性动力吸振器具有较宽的稳定控制范围和良好的减振效果.但对于参数的优化选择，上述文献仅采用试探法进行验证选择.文献[5-6]通过对全部状态变量进行反馈，设计二次最优控制律对时滞悬挂系统进行控制，可有效抑制外界扰动，提高车辆性能，然而在二次型指标泛函中，加权系数矩阵的选择也是依靠经验和试探得到的,具有一定的局限性.本文采用部分状态进行反馈控制，利用傅里叶变换在频域内建立确定的减振目标优化函数，在稳定区域内通过最优化方法选择最优的反馈增益系数和时滞量，使得目标函数值最小，从而提高悬架的减振性能，改善车辆的平顺性.

1力学模型

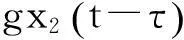
由牛顿第二定律可知，系统的运动微分方程为

(1)

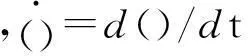
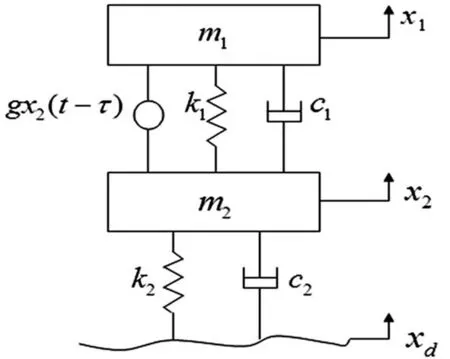
图1　含时滞反馈控制的1/4车辆悬架系统模型

表11/4车辆悬架参数

车身质量车轮质量悬架刚度系数轮胎刚度系数悬架阻尼系数轮胎阻尼系数m1/kgm2/kgk1/N·m-1k2/N·m-1c1/N·s·m-1c2/N·s·m-134540.516000190000150020

2时滞系统的稳定性分析

(2)

式中，()′=d()/dt*

对运动微分方程组(2)作拉普拉斯变换，得到系统的特征方程

(3)

特征方程(3)可写成多项式形式，即

(4)

当时滞τ=0时，系统特征方程为

(5)

利用劳斯-胡尔维茨稳定性判据，得到系统稳定的充分必要条件为

(6)

式中，σ1=αβc+αc+c，σ2=-αgk+αγ+1+α+c2αβ，σ3=cαγ+αβc，σ4=αγ.

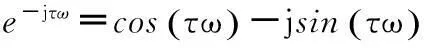
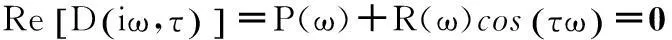
(7)

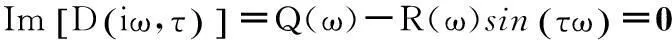
(8)

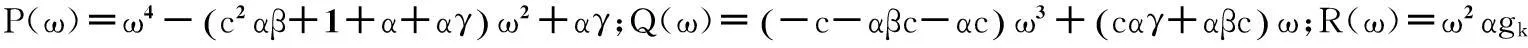
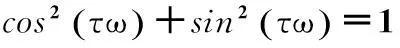
(9)

式中：

a1=-2α+α2β2c2+2α2c2β-2αγ+α2c2+2c2α+c2-2

a3=-2αγ-2α2γ-2α2γ2+α2β2c2+α2γ2c2

a4=α2γ2

根据多项式判别理论,对式(9)的根进行判别分类，利用稳定性切换的思想分析系统稳定性[7].如果方程(9)没有实根，说明随着时滞的增加，系统的特征根未穿越虚轴，系统稳定性不发生变化；如果式(9)有n个实根,令ω1>ω2>…>ωn>0，系统有临界稳定的特征根s=jωi，由式(7)、式(8)两式求得ωi对应的临界时滞τi,k

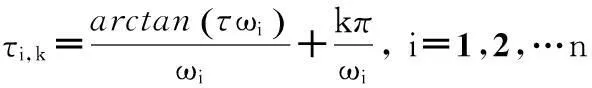
k=0,1,2…

(10)

式中φ∈(0,π),且满足

(11)

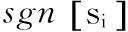
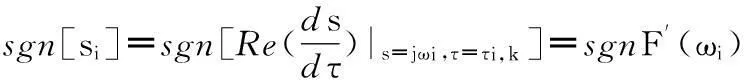
(12)

若sgn[si]=+1，说明时滞τ从左至右经过临界时滞τi,k时，特征根将穿越虚轴进入右半平面，系统不稳定特征根数目增加；反之，若sgn[si]=-1，特征根将穿越虚轴进入左半平面，系统不稳定特征根数目减少.根据系统特征根在临界时滞处的变化趋势，可得到系统的时滞稳定区域.

根据表1的系统参数，当时滞为零时，根据劳斯-胡尔维茨稳定条件(6),得到增益值gk<8.444 3时系统稳定，增益值gk≥8.444 3时系统不稳定；当时滞大于零时，利用多项式判别系统得到式(9)的实根与增益值gk的关系，见表2.

表 2 实根与增益值gk的关系

增益gk的范围(-?,-3.8682](-3.8682,3.8682)[3.8682,?)实根个数404

3控制参数的优化

车辆行驶过程中，路面不平是车辆振动的基本输入，其频率范围约为0.5～25Hz.车身共振频率大约在1～2Hz范围内，车身共振降低了车辆的平顺性.为优化悬架系统的减振性能，本文把车身加速度对路面速度激励的幅频特性函数作为目标优化函数，通过控制反馈增益值gk和时滞τ,降低车身在共振区域内的振动加速度.

对无量纲方程组(2)做傅里叶变换，可得到

(13)

式中

A11=-ω2+1+jω；

A12=-1-jω+gke-jτω；

A21=-α-jαcω；

目标优化函数为车身加速度对路面速度激励的幅频特性，即

(14)

为优化反馈增益值gk和时滞τ，减小车身共振范围内的车身加速度，可将无量纲化后的车身质量部分的固有圆频率代入式(14),获得仅含有gk,τ两个控制变量的目标函数，用MATLAB优化工具箱对目标函数进行优化分析，得到最优控制参数.

经优化后得到(gk,τ)=(-1.214 7,2.349 9)是目标函数的最小值点.由系统稳定性分析可知，gk=-1.214 7满足系统稳定性充要条件(6)，同时gk=-1.214 7落入区间(-3.868 2,3.868 2)，系统是全时滞稳定的.所以优化得到的控制参数是可取的.

4系统动态响应分析

4.1频域特性

将优化的控制参数转换到原时间尺度下，得到原悬架系统的最优反馈增益g=-19 435(N/m),时滞τ=0.345 1s.把方程组(1)作傅里叶变换，可以得到车辆3个振动响应对路面速度激励的幅频特性.图2～图4给出3个振动响应的幅频特性曲线，并与无反馈控制的被动悬架作对比.

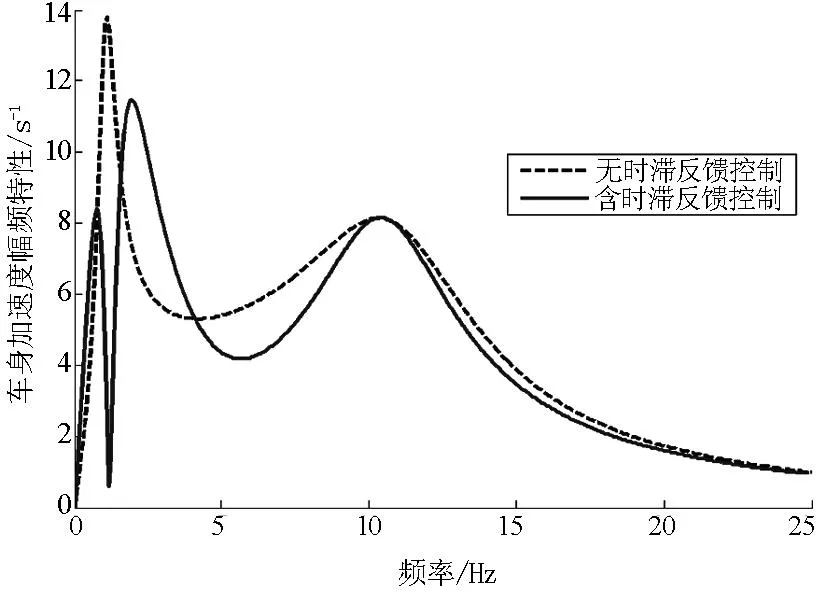
图2　车身加速度幅频特性曲线

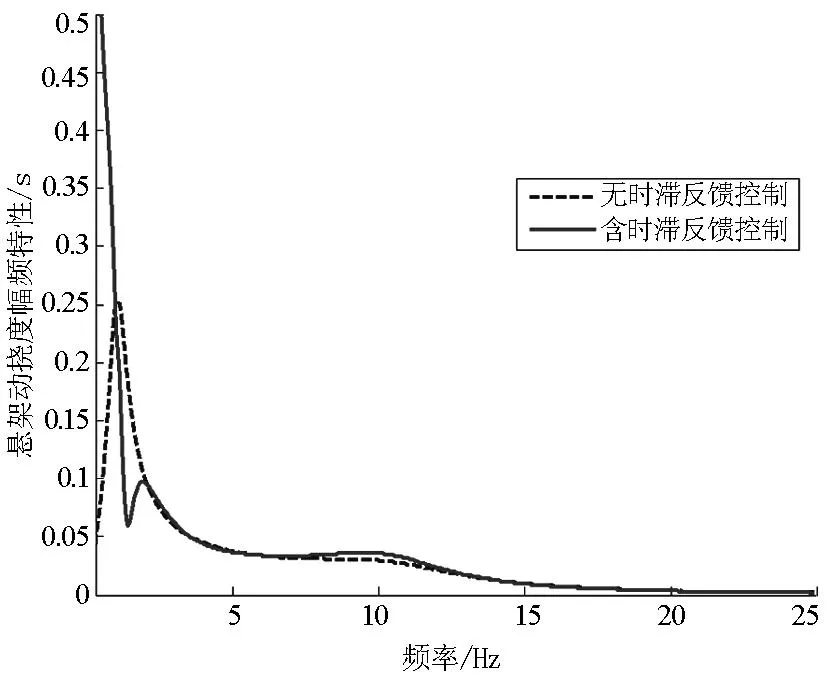
图3　悬架动挠度幅频特性曲线

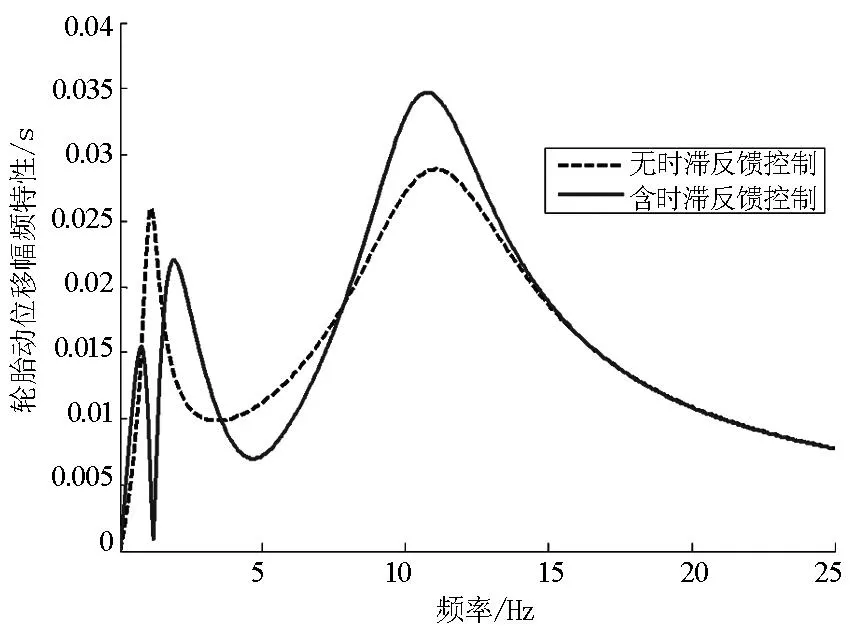
图4　轮胎动位移幅频特性曲线

从图2～图4看出，时滞对车身振动有较大的影响.与被动悬架相比，在接近车身共振的(1～2Hz)频率范围内，含时滞反馈控制的车辆车身加速度、悬架动挠度和车轮动位移都显著减小；在人体敏感的频率(4～12.5Hz)范围内,车身加速度降低，悬架动挠度基本没变化，车轮动位移先减小后增大；在12.5～25Hz范围内，两种悬架的减振效果差别不大.

4.2时域响应仿真

在MATLAB/Simulink模块中对系统振动响应作时域仿真.以简谐激励xd=0.05sin(2.12πt) 模拟路面输入，xd为路面不平度(m)，激励频率接近车身固有频率,振动响应量的时域仿真如图5～图7所示.

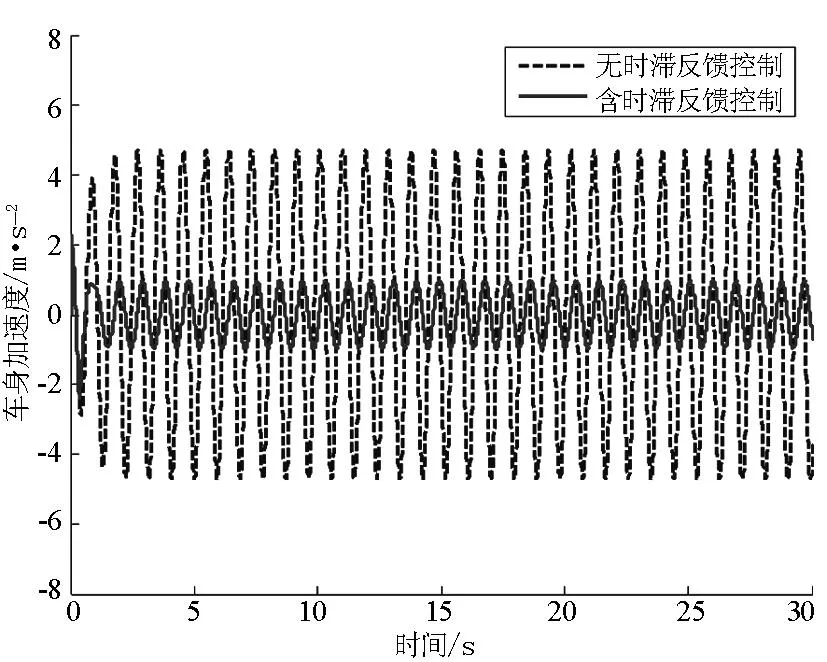
图5　车身加速度响应

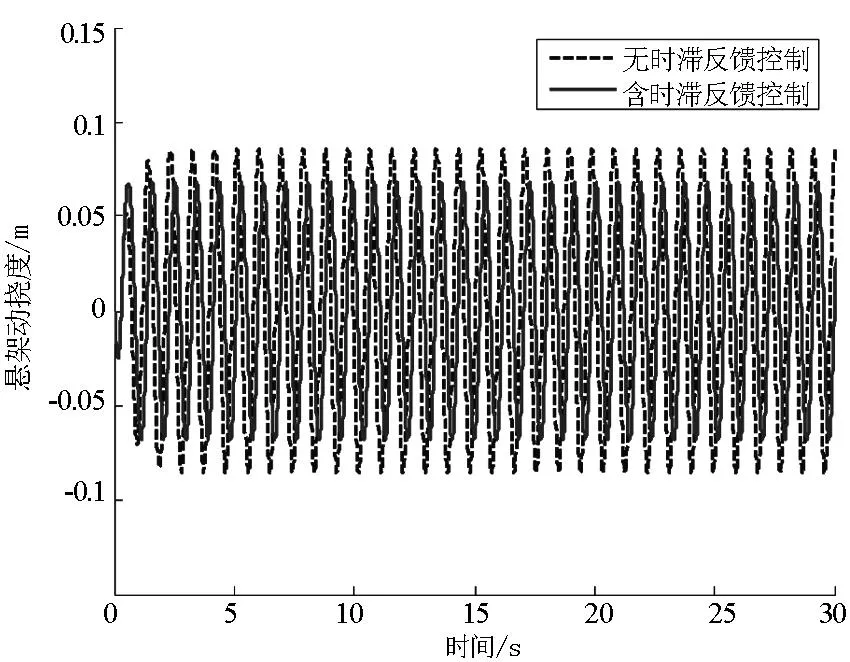
图6　悬架动挠度响应

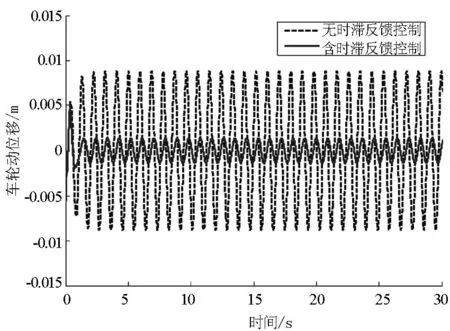
图7　车轮动位移响应

从图5～图7看出，相比被动悬架，路面激励频率接近车身固有频率时，车身加速度和车轮动位移明显减小，悬架动挠度也有所减小，说明时滞反馈控制能有效地提高悬架系统的减振性能和轮胎的接地性，提高了车辆的平顺性.

5结束语

本文研究了含时滞反馈控制的车辆悬架系统，利用稳定性切换的思想分析系统稳定性，在频域内建立车身加速度的目标优化函数，对控制参数进行优化.仿真结果表明，时滞反馈控制能有效降低车身加速度，提高车辆悬架的减振性能,从而改善车辆的平顺性.

参考文献：

[1]胡海岩,王在华.非线性时滞动力系统的研究进展[J].力学进展,1999,29(4): 501-512.

[2]OlgacN,Holm-hansenBT.Anovelactivevibrationabsorptiontech-nique:delayedResonator[J].JournalofSoundandVibration,1996, 176(1):93-104.

[3]赵艳影,徐鉴.时滞非线性动力吸振器的减振机理[J].力学学报，2008,40(1):98-105.

[4]赵艳影,徐鉴.时滞反馈控制在自参数动力吸振器中的作用[J].固体力学学报，2007,28(4):109-116.

[5]LeiJ,TangGY.Optimalvibrationcontrolforactivesuspensionsystemswithactuatorandsensordelays[C]//ProceedingsofIEEEInternationalConferenceonSystems,Man,andCybernetics.2008:2 828-2 833.

[6]TangGY.Feedforwardandfeedbackoptimalcontrolforlinearsystemswithsinusoidaldisturbance[J] .HighTechnologyLetters[J].2001,7(4):16-19.

[7]WangZH,HuHY.Stabilityswitchesoftime-delayeddynamicssystemswithunknownparameters[J].JournalofSoundandVibration，2000,233(2),215-233.

(编辑：郝秀清)

Research on vibration reduction of 1/4 car model with time delay feedback control

ZHU Kun, REN Chuan-bo, WANG Fei， QU Yu-wen

(School of Transportation and Vehicle Engineering, Shandong University of Technology, Zibo 255049,China)

Abstract:A 1/4 car suspension model with time-delay state feedback control is built, the stability analysis of the suspension system is discussed by using the stability switching method. The system vibration performance in frequency domain is studied and the car body acceleration amplitude frequency characteristics is used as objective function, with the aid of MATLAB optimization toolbox, the optimal feedback gain coefficients and time delay are obtained. The simulation results in MATLAB/Simulink module show that the time delay feedback control can effectively suppress vibration and improve vehicle ride comfort.

Key words:delayed feedback ; stability switch; amplitude frequency characteristics; MATLAB/Simulink；vehicle ride comfort

中图分类号：O328;TB123

文献标志码：A

文章编号：1672-6197(2016)02-0031-05

作者简介:朱坤，男，zhukun0213@126.com; 通信作者： 任传波，男，chuanbor@sdut.edu.cn

基金项目：国家自然科学基金项目(51275280)

收稿日期：2015-01-08