基本解法在三维涂层结构温度场中的应用

公颜鹏， 周爱华， 张耀明

(山东理工大学 理学院， 山东 淄博 255049)



基本解法在三维涂层结构温度场中的应用

公颜鹏， 周爱华， 张耀明

(山东理工大学 理学院， 山东 淄博 255049)

摘要：研究三维涂层结构温度场问题的基本解法,给出求解此类问题的新途径,同时也拓展了基本解法的应用范围.对结构厚度小到1×10-10的涂层结构温度场问题进行了研究,所取得的数值结果与精确解相当地吻合,表明基本解法是求解涂层结构温度场问题的强有力工具,且方法简单、易于程序设计.

关键词：基本解法; 涂层结构; 温度场

随着现代材料科学技术的发展以及实际工程的需要,具有耐高温、耐氧化、耐磨损、抗腐蚀等优良特性的涂层结构愈来愈引起人们的重视,其应用范围已涉及汽车、航空、建筑、陶瓷、刀具制造等诸多领域[1-3].然而,一般涂层材料的厚度较薄,约在微米级甚至纳米级,受其厚度尺寸的限制,涂层材料中物理量的数值分析一直是工程中的难点.有限元法是常用数值分析方法,采用有限元法计算时,为了避免畸形单元，必须按照结构的厚度划分网格,这将导致百万甚至几百万个离散单元，计算工作量剧增[4].边界元法可有效地处理涂层问题[5-6],但需要处理复杂的几乎奇异积分.

基本解法(MFS)是由Kupradze和Aleksidze[7]在1964年提出的，它具有精度高、收敛速度快、程序设计简单、无需对区域和边界划分网格、无需计算奇异及几乎奇异积分、适合处理复杂区域和高维问题等诸多优点，已广泛应用于固体力学、流体力学及热传导等问题的求解，取得了很好的效果. 然而，基本解法在三维涂层结构问题中的应用至今仍鲜有报道. 本文研究三维涂层结构温度场问题的基本解法，为该类问题的研究开辟新的途径，拓展其应用领域.

1三维位势问题的基本解法

本文假定Ω是R3中的一个有界区域,Γ=∂Ω是其边界. n=(n1,n2,n3)是区域Ω的边界Γ在x点处的单位外法向量.在边界外部选取N个源点yj,j=1,2,…,N，则计算点x处的位势为

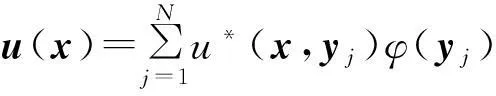
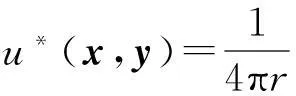
若在边界Γ上选取M个配置点xi,i=1,2,…,M,则边界配置点处的位势和法向梯度可表示为

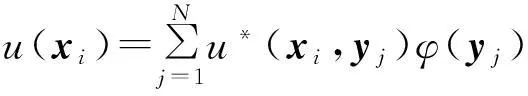
(1)

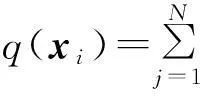
(2)

2三维涂层问题的基本解法

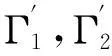
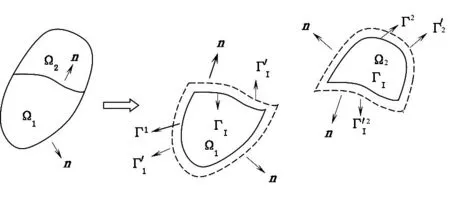
图1　分域法结构图

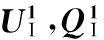
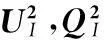
由方程(1)、(2), 在Ω1上可建立如下矩阵方程:

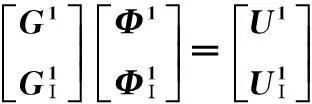
(3)

同理, 在Ω2上可建立如下矩阵方程:

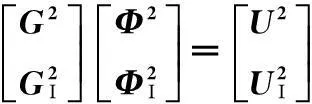
(4)

对于适定的边值问题,或者边界上的温度已知或者法向梯度已知. 边界离散化后, 每个节点上都会产生一个代数方程, 方程的个数与虚边界节点处待求密度函数的个数相同, 因而可以数值求解. 分域法将区域Ω1与Ω2看成两个独立的问题来处理, 在各自区域上利用虚边界元法进行计算, 但在Ω1与Ω2的共同边界ΓΙ上, 温度与温度梯度都是未知的, 因此未知参量的个数大于代数方程的个数. 要使得边值问题可解,必须引入如协调条件：

(a)边界ΓΙ上的温度协调条件

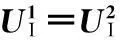
(5)

(b)边界ΓΙ上的热流协调条件

(6)

若边界Γ1,Γ2上节点的位势已知, 根据条件(5)和(6), 式(3)和式(4)可合并成

(7)

若边界Γ1,Γ2上节点的位势梯度已知, 根据条件(5)和(6), 式(3)和(4)可合并成

(8)

类似地, 可写出混合边界条件相应的方程组.

式(7)或式(8)即为涂层结构温度场虚边界元法的基本列式. 通过式(7)或式(8), 可求出Ω1与Ω2虚边界上的节点密度函数,进而可以利用内点积分方程求出内点的物理参量.

显然,以上过程可以直接推广到多涂层结构问题,只是联立方程的个数有所增加,这里就不再过多阐述.

3数值算例

考虑2个涂层结构的数值算例来验证本文方法的有效性. 为了表明方法数值解的准确性, 定义平均相对误差

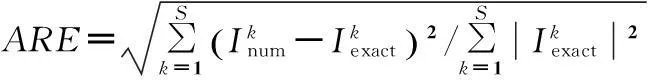
(9)

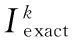
算例1研究球壳涂层结构的热流问题. 图中2(a)、2(b)是本文考察的空心球壳结构及网格模型. 图3(b)是球壳涂层结构被x2x3平面切割的截面图, 图3给出了涂层结构及虚边界计算模型被x2x3平面切割的截面图. 基体是一内半径为r1=1, 外半径为r2=2的球壳, 涂层外径为r3. 涂层厚度记为δ=r3-r2. 边界条件如图3(a)所示, 基体内表面温度为10°C, 涂层外表面温度为20°C. 基体导热率为k1=1,涂层导热率为k2=2.

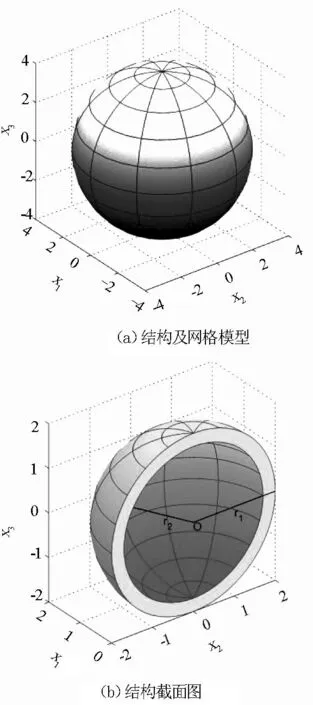
图2　空心球壳结构

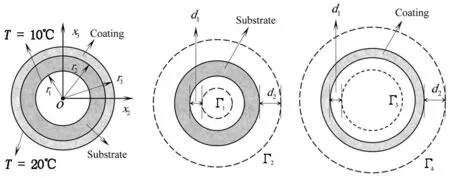
图3　球壳涂层结构的热流问题截面图

定义涂层区域特征值最小尺寸与最大尺寸之比δ=(r3-r2)/r1为狭长比. 计算此模型时, 我们将每个虚边界均划分为64个单元, 总共256个单元. 为了更全面地反映方法的计算精度, 在基体与涂层接触面上选取均匀分布的64个计算点, 并且虚实边界距离设定为d1=0.4,d2=10. 图4给出了不同狭长比下,即δ从10-1到10-10变化时, 涂层与基体接触面上温度与热流量的平均相对误差的变化曲线. 由图4可以看出, 利用该方法计算的结果精度很高, 即使狭长比到10-10也能得到很理想的结果. 此外, 图5(a)、5(b)给出了狭长比δ=1.0×10-7时, 接触面上所取计算点的温度解与热流数值解的相对误差曲面，可看出数值结果的相对误差相当地小. 表明该方法非常有效.

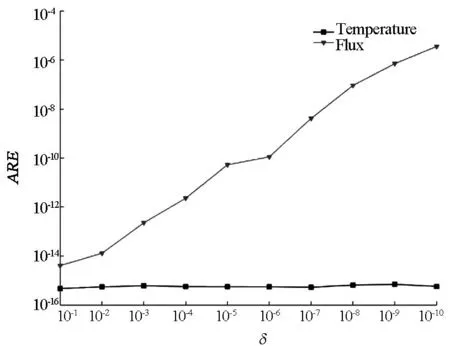
图4　接触面温度与热流量数值解的平均相对误差

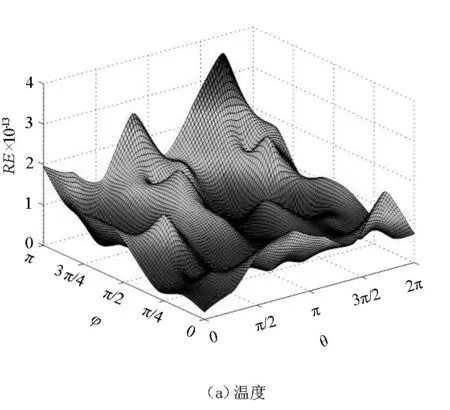
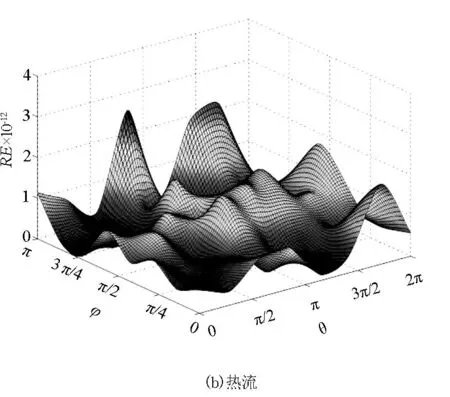
图5　涂层与基体接触面温度与热流解的相对误差曲面

图6给出了在狭长比与虚实边界距离不变的情况下, 随着单元数的增加, 基体与涂层接触面上所取计算点处的温度解、热流解的平均相对误差变化曲线即收敛曲线. 可以看出, 随着单元数的增加,相对误差迅速减小, 说明该方法具有良好的收敛性.

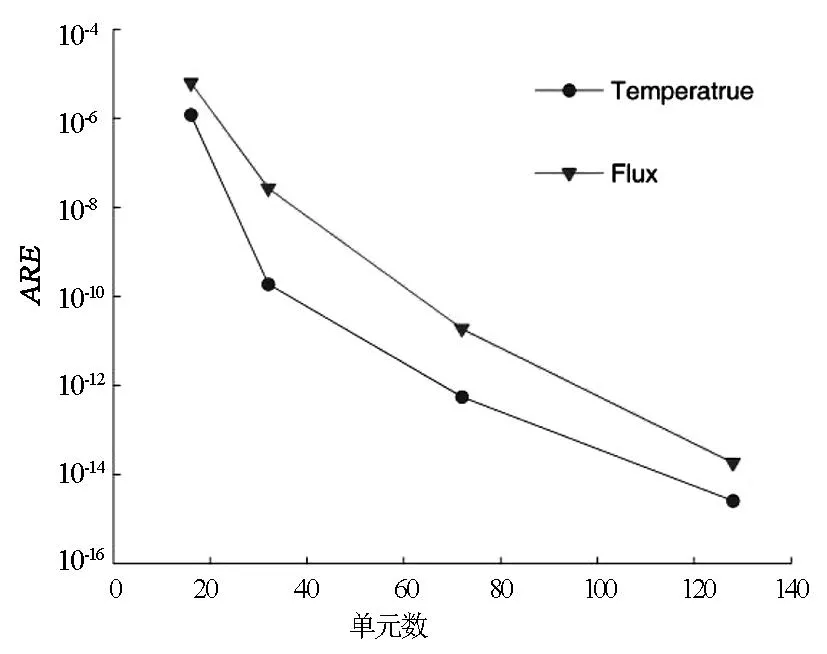
图6　接触面温度解与热流解的收敛曲线

算例2薄板涂层结构的热传导问题. 如图7(a)所示, 基体长L=2, 高H=0.1, 涂层厚度为h. 已知基体下表面温度为10°C, 涂层上表面温度为20°C, 其余各侧面热流q=0. 基体导热率为k1=1,涂层导热率为k2=2.

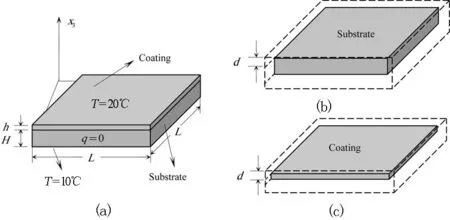
图7　薄板涂层结构图

取虚边界与结构外表面的几何形状相似. 图7(b)给出基体结构及虚边界计算模型, 图7(c)给出涂层薄体结构及虚边界计算模型. 基体虚实边界间的距离与涂层虚实边界间的距离已在图7(b)与图7(c)中标示. 基体上、下虚边界以及涂层上、下虚边界均划分为64个单元,其余各侧面虚边界均划分为8个单元, 共320个单元, 即本模型共有320个配点. 为了更全面地反映方法的计算精度, 在基体与涂层界面上及涂层上表面各选取均匀分布的400个计算点. 当涂层的厚度h从1×10-1变化到1×10-9时, 虚实边界间的距离分别取d=2、 20、 40,图8与图9分别给出了界面上计算点处的温度解和热流解的平均相对误差变化曲线. 可看出,d=20和d=40时,数值解的精度非常高,d=2时,解的精度较差,但精度仍可接受. 表明虚实边界间的距离选取范围非常地宽泛.

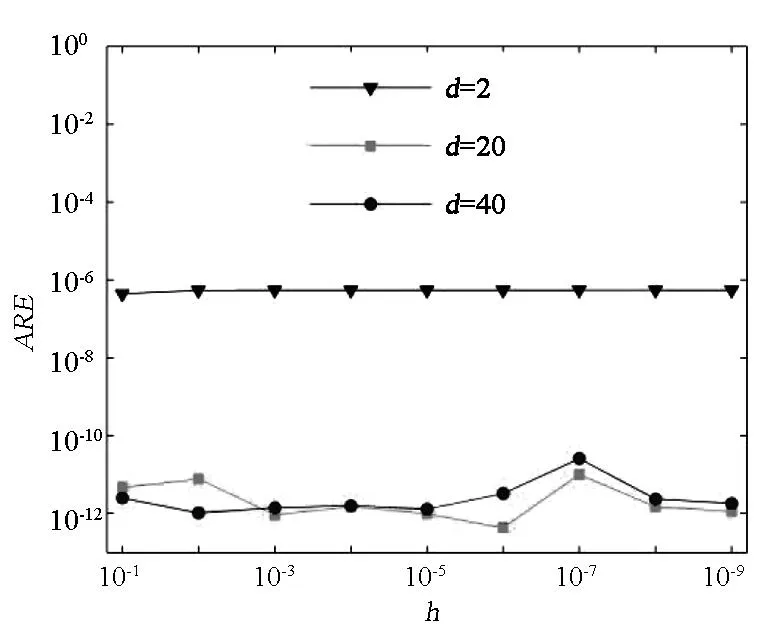
图8　界面上温度解的平均相对误差

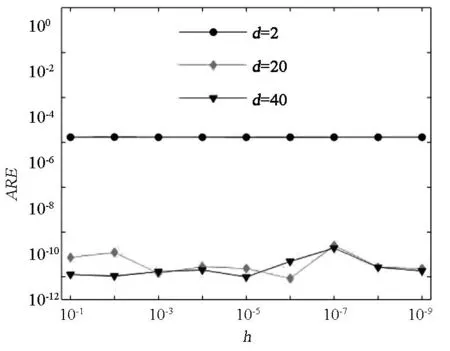
图9　界面上热流解的平均相对误差

单元划分情况不变, 取涂层厚度为10-9, 虚实边界距离为d=10, 图10(a)、10(b)分别给出了界面上所取400个计算点处的温度解与热流解的相对误差曲面；可看出, 数值结果的相对误差都非常地小. 表明该方法能够准确高效地求解厚度小到纳米级的涂层温度场问题.

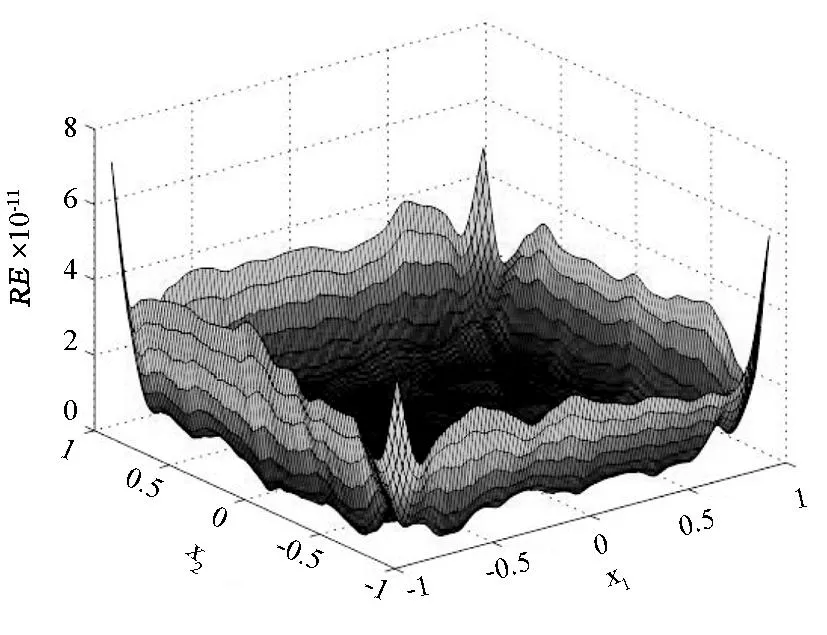
(a)温度

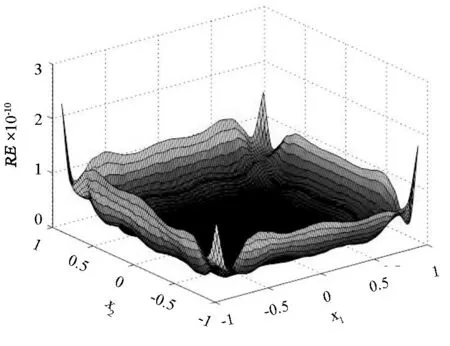
(b)热流图10　涂层与基体接触面温度与热流解的相对误差曲面

另外，图11给出了在节点数目相同的情况下，分别用边界元(BEM)和基本解法(MFS)计算接触面上温度时平均相对误差(ARE)随涂层厚度的变化情况.容易看出，虽然两种方法都能得到比较好的结果，但是本文解法(MFS)的精度比边界元法高出好几个数量级.表明本文方法在处理涂层问题时，比边界元法在精度上有很大优势.

4结束语

本文研究基本解法求解三维位势涂层结构温度场问题, 给出求解涂层结构温度场问题的新途径,拓展了基本解法的应用范围. 数值算例表明, 基本解法是求解涂层结构温度场问题的强有力工具, 即使结构的厚度小到10-10, 依然可获得高精度的数值解.

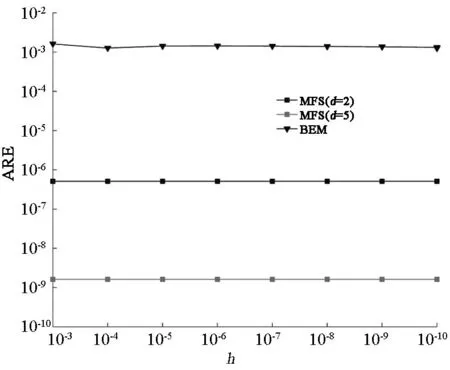
图11　涂层与基体接触面温度的平均相对误差随涂层厚度的变化情况

参考文献：

[1]胡传炘. 特种功能涂层[M]: 北京：北京工业大学出版社, 2009.

[2]杨晓光, 耿瑞, 熊昌炳. 航空发动机热端部件隔热陶瓷涂层应用研究[J]. 航空动力学报, 1997, 12(2): 183-188 .

[3]胡兴军. 刀具表面涂层技术进展综述[J]. 产品与技术, 2008, 12(6): 91-94.

[4]LuoJF,LiuYJ,BergerEJ.Analysisoftwo-dimensionalthinstructures(frommicro-tonano-scales)usingtheboundaryelementmethod[J].ComputationalMechanics, 1998, 22(5): 404-412.

[5]张耀明, 谷 岩. 涂层结构中温度场的边界元解[J]. 固体力学学报, 2011, 32(2): 133-141.

[6]程长征, 牛忠荣, 周焕林,等. 涂层结构中温度场的边界元法分析[J]. 合肥工业大学学报(自然科学版), 2006, 29(3): 326-329.

[7]KupradzeVD,AlerksidzeMA.Themethodoffunctionalequationsfortheapproximatesolutionofcertainboundaryvalueproblems[J].USSRComputationalMathematicsandMathematicalPhysics, 1964, 4(4): 82-126.

(编辑：郝秀清)

Method of fundamental solutions of the temperature field in 3D coating structures

GONG Yan-peng, ZHOU Ai-hua, ZHANG Yao-ming

( School of Science, Shandong University of Technology, Zibo 255049, China)

Abstract:The method of fundamental solutions (MFS) for solving coating problems in 3D potential theory is developed, which not only provides a new approach to deal with such problems but also extends its application fields. Numerical examples demonstrate that the proposed method can effectively solve coating structure problems even when their thicknesses are as small as the nanometer scale, showing that the MFS is a simple and powerful tool for solving 3D coating problems.

Key words:MFS; coating structures; temperature field

中图分类号：O342

文献标志码：A

文章编号：1672-6197(2016)02-0013-05

作者简介：公颜鹏, 男, gyp2011@sina.com; 通信作者： 张耀明, 男, zymfc@163.com

基金项目：山东省自然科学基金重点项目(ZR2010AZ003)

收稿日期：2015-03-07