实施干预措施在HIV/AIDS预防中的效果

王来全， 魏成花, 夏米西努尔·阿布都热合曼

(1.昌吉职业技术学院 基础部， 新疆 昌吉 831100; 2.昌吉学院 数学系， 新疆 昌吉 831100；

3.新疆大学 数学与系统科学学院, 新疆 乌鲁木齐 830046)



实施干预措施在HIV/AIDS预防中的效果

王来全1， 魏成花2, 夏米西努尔·阿布都热合曼3

(1.昌吉职业技术学院 基础部， 新疆 昌吉 831100; 2.昌吉学院 数学系， 新疆 昌吉 831100；

3.新疆大学 数学与系统科学学院, 新疆 乌鲁木齐 830046)

摘要：考虑了一类对高危人群实施干预措施的HIV/AIDS传播模型,给出了无病平衡点的全局稳定和地方病平衡点的局部稳定的条件.当R0>1时,讨论了地方病平衡点的局部渐进稳定性,重点讨论了对高危人群实施干预措施在HIV/AIDS预防中的积极效果.

关键词：艾滋病; 干预措施; 基本再生数; 渐近稳定; 效果

目前还没有有效的使艾滋病患者痊愈的药物.近几年,在吸取传统单一的抵抗生素消炎法的基础上,医生们探索采用复合疗法,但这种方法在一些艾滋病的高发区很难实现推广.考虑到当地人群的收入情况、地理分布、科学技术等需求和含量,我们不得不采取比较有效、直接并且具有经济效益的干预措施来实现对艾滋病的预防.

为了揭示传染病的传播规律，预测流行趋势,作为传染病和数学理论交叉学科的传染病数学模型迅速发展起来,许多学者对传染病模型进行了研究，并从中得到很好的结果.文献[1-2]建立并研究了一类HIV/AIDS传播模型,文献[3]研究了一类公众教育活动对预防HIV/AIDS的影响.基于文献[4-5]的理念,文献[6]研究了对一些易感者实施单一的教育活动对预防HIV/AIDS传播的影响.但是,很少有人研究一类对高危人群实施干预措施的时滞HIV/AIDS传播模型,并进一步说明干预措施在HIV/AIDS预防中的积极效果.假设把易感人群分为高危易感人群和低危易感人群，在高危易感人群感染率大于低危易感人群的情况下,假设只对高危人群实施干预措施,讨论地方病平衡点的局部渐近稳定性,重点研究对高危人群实施干预措施在预防HIV/AIDS传播中的效果，进一步证明在艾滋病的高发期和蔓延期推行预防干预措施的必要性.

1模型的建立

讨论的数学模型如下:

(1)

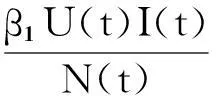
2平衡点和基本再生数

显然,系统(1)存在一个无病平衡点E0(U0,S0,0,0).其中：

应用计算基本再生数的标准方法，计算出系统(1)的基本再生数R0.

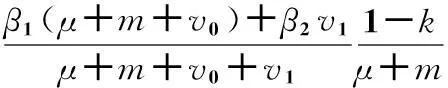
当R0>1时，系统(1)存在一正地方病平衡点E1(U1,S1,I1,A1`).

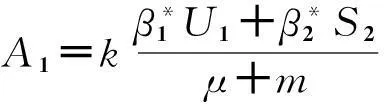
此时

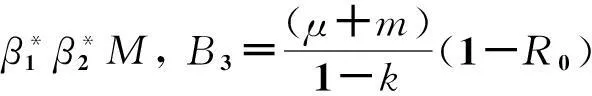
系统(1)的解集Ω和解的正性,无病平衡点E0(U0,S0,0,0)的渐近稳定性,与文献[7]的研究方法类似.下面就系统(1)的地方病平衡点的局部稳定性和地方病的持久性进行讨论.

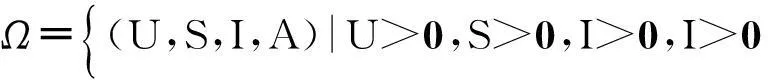
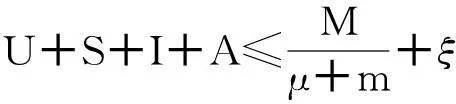
3地方病平衡点的局部渐进稳定性

为了分析地方病平衡点的局部渐进稳定性,令:x(t)=U(t)-U1,y(t)=S(t)-S1,z(t)=I(t)-I1,w(t)=A(t)-A1.则系统(1)在点E1(U1,S1,I1,A1`)处可以得到线性近似方程. 也就是说通过讨论系统(1)在点E1(U1,S1,I1,A1`)处的线性近似方程在平衡点(0,0,0,0)处的全局渐近稳定性来讨论系统(1)在地方病平衡点E1(U1,S1,I1,A1`)处的局部渐近稳定性[5]

假设Hi(i=1,2,3…6)为τ的有界函数,构造Lyapunovh函数

V(x,y,z,w)={x(t)+y(t)+z(t)+w(t)}2

沿着系统系统(1)在点E1(U1,S1,I1,A1`)处的线性近似方程对V(x,y,z,w)求导数得

V′(x,y,z,w)=2{x(t)+y(t)+z(t)+w(t)}×

{x′(t)+y′(t)+z′(t)+w′(t)}=-2(μ+m)×

{x(t)+y(t)+z(t)+w(t)}2≤0

当R0>1时，得到V(x,y,z,w)=0当且仅当x(t)=y(t)=z(t)=w(t)=0.根据Lyapunov-Lasalle定理:地方病平衡点E1在Ω局部渐近稳定,得到如下定理:

定理1如果R0>1,那么系统(1)的地方病平衡点E1(U1,S1,I1,A1`)局部渐进稳定.

4对高危人群实施干预措施在HIV/AIDS预防中的效果

一般的干预措施主要有:在公共场所推广使用安全套 ,对吸毒者开展美沙酮维持治疗和清洁注射针具交换等措施,用来减少被二次感染HIV/AIDS的几率.在传染病学中,基本再生数R0是用来区分疾病流行与否的阈值,所以我们对模型(1)的基本再生数R0的相关参数:干预措施v0与R0的关系进行讨论.对R0关于干预措施v0求导数得

(2)

类似的,下面讨论模型(1)的基本再生数R0的相关参数:艾滋病的潜伏期τ与R0的关系,对R0关于艾滋病的潜伏期τ求导数得

(3)

显然,基本再生数R0关于干预措施v0为单调递减的函数,从而说明对高危易感人群实施有效干预措施可以减少HIV/AIDS疾病的蔓延.同理,由(3)式可知,艾滋病的潜伏期τ与R0成单调增加关系,进一步说明了艾滋病的潜伏期加快了疾病的流行,这一结论与文献[7]类似.

5结束语

考虑了一类具有干预措施的HIV/AIDS传播模型,应用HIV/AIDS数学模型评估了在高危人群中实施干预措施对预防HIV/AIDS传播的影响,由(3)式可知：对高危人群增强干预措施可以预防HIV/AIDS的蔓延,从而可以减少被二次感染的几率,如果本文的干预措施是教育和疫苗,则结果与文献[6]和[8]一致.尽管目前的医疗技术还无法治愈艾滋病,但只要认真进行不良行为干预,就能有效遏制艾滋病对人类的危害.通常通过推广使用安全套、为吸毒人群提供清洁针具及药物替代疗法等方法进行艾滋病行为的干预，帮助有易感感染艾滋病病毒危险行为的人群改变行为,但是由于会受到社会各种压力和歧视,同性恋、吸毒等不良行为均十分隐蔽,干预起来难度大,所以只有结合实际情况制定可行措施积极推行预防艾滋病干预措施的实施,方能有效防控艾滋病的传播.

参考文献:

[1]MeleanAR,BlowerSM.Modellingvaccination[J].TrendsMicrobiol, 1995,3:458-463.

[2]NyabadzaF.AmathematicalmodelforcombatingHIV/AIDSinsouthernAfriea:Willmultiplestrategieswork[J].BiolSyst,2006,14：357-372.

[3]HassardDD,KazarinoffND,WanYH.TheoryandapplicationsofHopfbifurcation[M].Cambridge：CambridgeUniversityPress，1981.

[4]SongX,ChengS.Adelay-differentialequationmodelofHIVinfectionofCD4+Tcell[J].J.KorealMath.Soc, 2005，42:1 071-1 086.

[5]ZhangTL，jiaMH,LuoHB, et al.StudyonaHIV/AIDSmodelwithapplieationtoYunmanprovince,China[J].AppliedMathematicalModelling.2011,35：4 379-4 392.

[6]MukandavireZ,GariraW,TchuencheJM.ModellingeffectsofpublichealtheducationalcampaignsonHIV/AIDStransmissiondynamics[J].AppliedMathModelling, 2009, 33:2 084-2 095.

[7]MukandavireZ,GariraW,ChiyakaC.AsymptoticpropertiesofaHIV/AIDSmodelwithatimedelay[J].Math.Appl.2007,330:916-933.

[8]HaoPM,FanDJ,WeiJJ, et al.DynamicbehaviousofadelayedHIVmodelwithstage-strueture[J].CommumNonlinearSeiNumerSimulat,2012,17:4 753-4 766.

(编辑：郝秀清)

Implementation of intervention measures for HIV/AIDS prevention effect

WANG Lai-quan1, WEI Cheng-hua2， Xamxinur Abdurahman3

(1.Department of Foundation, Changji Vocational and Technical College, Changji 831100, China；2.Department of Mathematics, Changji University， Changji 831100, China;3.College of Mathematics and System Science, Xinjiang University, Urumqi 830046, China)

Abstract:We considered a HIV/AIDS transmission model with intervention measures for high-risk susceptible. The basic reproduction number R0which determines whether the disease goes to extinction or not is obtained. we investigated the local stability of the endemic equilibrium, when the basic reproduction number R0is greater than 1. Furthermore, we investigated the positive effect of the intervention measures on the prevention of HIV/AIDS.

Key words:HIV/AIDS; intervention measures; basic reproduction number; stability; effect

中图分类号：O175.1

文献标志码：A

文章编号：1672-6197(2016)02-0036-03

作者简介：王来全,男,wanglaiquana@126.com

基金项目：国家自然科学基金项目(11261056); 昌吉职业技术学院自然科学科研课题(CJZY2015026)

收稿日期：2015-03-28