岩土二维真实细观数值分析方法研究

王伟 , 吴昊，何培玲,胡爱宇

(1. 南京工程学院建筑工程学院，江苏 南京 211167; 2. Department of Civil Engineering and Mechanics, University of Wisconsin-Milwaukee, Milwaukee 53211 USA;3. 南京工业大学浦江学院，江苏 南京 211816)



岩土二维真实细观数值分析方法研究

王伟1, 2, 吴昊3，何培玲1,胡爱宇1

(1. 南京工程学院建筑工程学院，江苏 南京 211167; 2. Department of Civil Engineering and Mechanics, University of Wisconsin-Milwaukee, Milwaukee 53211 USA;3. 南京工业大学浦江学院，江苏 南京 211816)

摘要：分析岩土细观应力特征，通过Ostu’s类判别法对水泥土初始状态细观图像进行二值化处理，经灰度形态学算子“腐蚀”、“闭合”运算，得到表征水泥土细观结构特征的二值图像. 然后通过边缘检测，几何矢量化转换成有限元软件识别的矢量图，形成水泥土二维真实细观有限元模型. 利用多孔弹性本构关系进行数值分析，结果表明：该研究揭示水泥土细观真实应力、变形的全场变化规律；定量分析水泥土的细观非线性力学特征，体现水泥土强度和变形的细观机理.

关键词：水泥土；真实细观模型；数字图像处理；数值模拟

0引言

岩土宏观力学性能在很大程度上受其细观结构控制，表现出的各种变形和强度特性是其内部各要素共同作用的结果. 因此，对细观结构演化规律的研究有利于对岩土材料微细观应力场和变形场变化的深刻认识，有利于改进土力学宏观本构关系的研究方法. 研究土体细观特征的变化规律有多种方法[1-3]. 一种是利用图像测试技术进行土体细观分析，如：Oda等用X-ray micro-CT得到砂土体系剪切带的细观结构[4]，方祥位等基于非饱和原状Q2黄土CT-三轴剪切试验分析细观结构演化变量与净围压和吸力的关系[5]，王伟等根据轴对称原理，利用光学显微成像设备采集岩土半圆柱形平面部分的细观图像，分析其细观参数如圆形度、分布分维及定向度等随载荷的演化规律[6]. 另一种是细观理论分析，如：沈珠江等基于岩土破损力学理论，提出岩土二元介质模型，探讨理想化结构性岩土材料的细观特性[7]，谢定义在考察土结构性能及其定量化指标研究现状的基础上，提出综合结构势的概念[8]. 还有一种是通过颗粒流或离散元法(DEM)来模拟岩土材料的细观特征，如：徐文杰为了更接近土-石混合体实际结构情况，开发基于任意凸多边形及椭圆形块石的土-石混合体细观结构随机生成系统[9]，蒋明镜等基于局部平衡理论，用离散元法定性研究颗粒转动对离散材料宏微观特性的影响[10]，Huang等利用DEM模拟颗粒土排水和不排水三轴试验，研究其微观特征的变化规律[11]. 由于随机模型并不能代表岩土的真实细观结构，Yue等将岩石、土-石混合体的细观图像与有限元结合，实现真实细观结构的数值分析[12]. 但岩石、土-石混合体与土自身的物理力学性质存在很大的差别，且二者采集的细观图像特点显然不同.本文中在已有的研究基础上，将岩土细观图像引入到土的有限元模型中进行数值分析，以便真实反映岩土细观力学机理.

1细观试验与图像处理

1.1细观试验为了将水泥土内部细观结构特征引入到有限元模型中，利用多孔弹性本构关系研究其细观结构应力-应变规律，必须先进行岩土的细观试验，具体方法见文献[6]，即基于轴对称原理，选取标准圆柱形土样的一半(获取方法：采用手掰开的方式，尽量保证土样初始的内部结构特征，如果利用刀具切开则很容易破坏其对称面上的内部结构)，然后利用光学显微镜采集岩土半圆柱形试样在无侧限压缩试验中初始状态下平面部分的细观图像，以水泥土为试样，图像放大倍率的标定系数为K=0.003 4 mm/pixel.如图1所示，右边细观图像是从左边半圆柱形对称面局部区域上采集到的. 此细观图像明显反应该区域水泥土颗粒集聚体和孔隙的真实分布(细观层面)，下一步将此分布引入到有限元模型中.

图1　初始细观图像的采

1.2图像处理建立含岩土细观特征的有限元模型，将岩土细观图像与有限元ABAQUS对接，使ABAQUS软件识别到细观图像的格式，建立具有岩土2D细观特征的有限元模型.目前采集到的图像不是矢量化图像，随着图像的放大会变得越来越模糊，不适宜直接采用.因此，对采集的细观图像需要进行下列处理.先利用中值滤波减少电子元件噪声的干扰和光照不均的影响，为下一步的图像二值化做准备. 由于网格只能在土颗粒集聚体中划分，二值化图像可以得到较准确的土颗粒集聚体和孔隙之间的边界，便于实现有限元网格自动划分. 由于该图像具有背景和目标不明显的特点，利用常规的灰度直方图进行二值化，效果不理想. 因此，采用自动判断阈值的Otsu’s类判别分析法进行二值化，此方法不仅避免了人为因素的干扰，而且可以实现自动运算，获得类间方差的最大阈值，实现土颗粒集聚体和孔隙的真实边界.该阈值的计算公式见式(1)：

(1)

其中，

式中，Ave：灰度均值，i：灰度级(0≤i≤255)，Phs(i)：灰度级的概率函数，k：阈值，Aver(k)：灰度类均值，W(k)：类直方图和，Q(k)：类分离指标.

找到使Q取最大时的k值，即可得出最佳阈值T=k-1. 经过图像计算，该类间方差阈值为0.41，此阈值的含义与灰度直方图二值化的阈值不同.通过Otsu’s类判别法得到的二值化图像如图2所示，白色表示土颗粒集聚体，黑色表示孔隙. 由图2可见，土颗粒集聚体和孔隙的特征分布被真实地反映出来，与原始图像(图1右边细观图像)基本一致. 经二值化处理后的图像中有一些孤立点和很小的区域，这些仍然是孔隙，因二值算法自身的局限性，无法清晰分辨. 因此，还需要结合灰度形态学算子“腐蚀”和“闭合”运算对土颗粒集聚体和孔隙之间的边界进行平滑，使其分布特征更逼近原始结构. 经灰度形态学算子处理后的二值化图像见图3所示.

图2　Qstu’s方法得到的二值化图

图3　灰度形态学算子处理后的二值化图

有限元模型是矢量图，得到土颗粒集聚体和孔隙二值图像后，还需将图像矢量化，通过矢量化软件CORELDRAW将数字图像转换成矢量图像，以保证图像在倍数放大或缩小时仍保持图像原来的线条特征.有限元可以识别DXF格式的文件，将矢量图像存成DXF格式，将岩土真实的多孔性引入到有限元模型中. 然后根据细观试验的标定系数，将图像尺寸变换成实际度量尺寸而非像素尺寸，与有限元建模时通用的度量单位保持一致，建立包含岩土真实细观特征的有限元数值模型.

2多孔非线性数值分析及结果

本文中建立岩土真实细观特征的数值模型，利用多孔介质弹性理论对其进行分析，平均应力是体积应变的指数函数，用式(2)表示：

(2)

利用三轴试验得到的水泥土初始孔隙比和泊松比，根据无侧限压缩试验条件，对有限元模型进行材料性质、截面特征和边界约束的设定，经有限元网格的自动划分，进行多孔非线性数值分析. 经计算和分析得到如下结果：

1) 数值结果直观显示整个研究区域全场的Mises应力云图，如图4所示.从整个区域的应力分布可以看出，受真实孔隙形状的影响，该模型中出现明显的应力集中区，如图4中1、2、3位置所标注的区域，应力集中区易首先破坏，导致该处的土颗粒集聚体破碎，且可能与周围土颗粒集聚体重新组合，孔隙形状发生变化，达到一种新的受力平衡. 受内部细观特性决定，图中应力分布的不均匀性直接反映土样内部实际的细观受力特征，与土体常规的宏观模型中均匀的应力分布不一致.

图4　全场Mises应力云

2) 图4中1、2、3位置区域处的平均应力-应变曲线分别如图5(a)、图5(b)、图5(c)所示. 显然，3个应力集中区域的平均应力-应变规律是非线性的，而线弹性阶段非常小. 同时，从细观角度看，由于3个位置处应力集中区的土颗粒集聚体形状不相同，因此，相同应变下不同应力集中区域的平均应力值不同，与非应力集中区(见图4中的位置4区域)的平均应力-应变规律(见图5(d)所示)相比，二者平均应力值的数量级相差约10倍. 对比土工试验得到的整个土样的应力-应变曲线(见图6所示)，也可以看出土体局部区域细观平均应力-应变的数量级明显高于整体土样的应力-应变数量级. 从细观层面上看，岩土宏观的力学特征是细观应力集中区域土颗粒集聚体经过不断的变形-破坏-重组的结果. 具体是部分土颗粒集聚体在高应力下发生剪切破坏，导致局部区域土颗粒集聚体重新调整，以适应外部载荷达到新应力状态下的平衡.

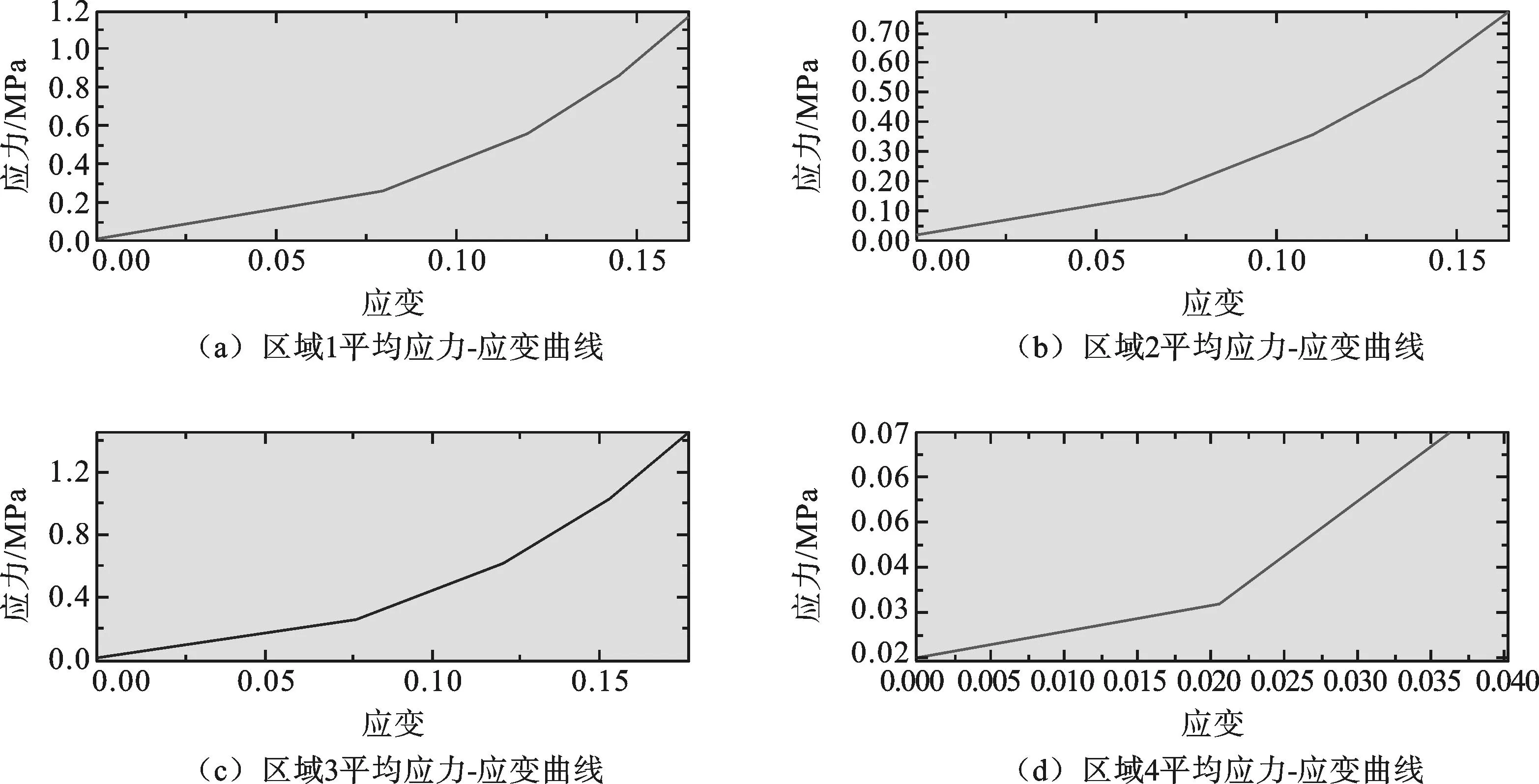
图5　四个区域处的平均应力-应变曲

图6　整个土样的应力-应变曲线

3) 数值结果也直观显示全场位移云图，见图7所示. 从图7中可以看出，整个区域的位移变化趋势以及不均匀性受孔隙形状和内部应力集中区域的影响，不同位置处位移由细观特征决定.数值计算结果显示右上角处位移量明显大于其他区域，这是右上角和右下角处较多的大孔隙共同影响的结果，可见水泥土细观结构对土体内部变形的重要影响，对下一步剪切带形成的研究可提供重要参考.

图7　全场位移云图

3结论

利用图像处理方法，结合有限元数值计算手段，实现包含水泥土真实细观特征的数值模拟和多孔非线性分析. 主要结论有：

1) 鉴于水泥土细观图像没有明显的背景特征，因此，采用Ostu’s类判别法进行图像二值化，结合形态学算子得到水泥土土颗粒集聚体和孔隙的实际分布特征. 然后通过几何矢量化及有限元建模实现包含水泥土真实细观结构的数值模型.

2) 基于多孔非线性有限元数值计算的结果，得到水泥土细观区域全场的Mises应力和位移分布图. 同时，分析局部不同的细观区域的非线性应力-应变关系，反映水泥土强度和变形的细观机理，为下一步包含细观特征的本构关系的研究奠定基础.

3) 细观应力云图直观反映土颗粒集聚体部分区域中存在应力集中区，导致该区域出现较大的应力集中，率先发生破坏的薄弱区. 因此，在载荷的作用下，土体内部部分应力集中区域的土颗粒集聚体经历不断的变形-破坏-重新组合的过程，调整受力状态以满足新状态下受力平衡，直至最终局部区域剪切破坏，此结果为进一步研究剪切带的细观机理提供思路.

4参考文献

[1] 孙其诚，程晓辉，季顺迎，等. 岩土类颗粒物质宏-细观力学研究进展[J].力学进展，2011, 41(3): 351-371.

[2] 王宇，李晓，赫建明，等. 土石混合体细观特性研究现状及展望[J]. 工程地质学报，2014, 22(1) :112-123.

[3] 尹振宇. 土体微观力学解析模型：进展及发展[J]. 岩土工程学报，2013, 35(6): 993-1009.

[4] Oda M, Takemura T, Takahashi M. Microstructure in shear band observed by microfocus X-ray computed tomography [J]. Geotechnique, 2004, 54(8): 539-542.

[5] 方祥位，申春妮，陈正汉，等. 原状Q2黄土三轴剪切细观结构演化定量研究[J]. 岩土力学，2010，31(1): 27-31.

[6] Wang Wei，He Xiaoyuan, Xiao Jianqiang, et al. Application of image tracking technology on microstructure research of lime solidify soil [C]. Proceedings of the SPIE-the International Society for Optical Engineering，2008, 7375, 73752I (5 pp) .

[7] 沈珠江, 刘恩龙, 陈铁林. 岩土二元介质模型的一般应力应变关系[J]. 岩土工程学报, 2005, 27(5): 489-494.

[8] 谢定义, 齐吉林. 土的结构性及其定量化参数研究的新途径[J]. 岩土工程学报, 1999, 21(6): 651-656.

[9] 徐文杰，胡瑞林，岳中琦.土-石混合体随机细观结构生成系统的研发及其细观结构力学数值试验研究[J]. 岩石力学与工程学报，2009,28(8):1652-1665.

[10] 蒋明镜，孙渝刚，张伏光. 基于微观力学的胶结岩土材料破损规律离散元模拟[J]. 岩土力学，2013，34(7): 2043-2050.

[11] Gu Xiaoqiang, Huang Maosong, Qian Jiangu. DEM investigation on the volution of microstructure in granular soils under shearing [J]. Granular Matter，2014，16: 91-106.

[12] Yue Z Q, Chen S, Tham L G. Finite element modeling of geomaterials using digital image processing[J].Computers and Geotechnics,2003, 30: 375-397.

(责任编辑郭定和)

Numerical analysis research on the 2D actual meso-structures of soil

WANG Wei1,2, WU Hao3, HE Peiling1, HU Aiyu1

(1. Institute of Civil Engineering and Architecture, Nanjing Institute of Technology, Nanjing 211167, China；2. Department of Civil Engineering and Mechanics, University of Wisconsin-Milwaukee, Milwaukee 53211, USA;3. Pujiang College,Nanjing Technology University, Nanjing 211816，China)

Abstract:In order to analyze the stress property of soil meso-structures, the meso-image captured before loading on the cement-soil half-cylinder sample has been processed binarily using the Ostu’s method. Then grey morphological operators such as “erosion”and“closing”also have been performed on the binary image, the distribution structures about soil particles and voids that form the inhomogeneity of the geomaterial in the image are identified.By the edge detection，vector transform are used to acquire the vectorized digital image which is the input document for the finite element software. So, the soil actual meso-model is established by the Finite Element Method. Using the porous media theory,we carry out numerical simulation, and the results show: 1) based on the meso-numerical analysis, this research can reveal the actual meso stress and deformation distributions of soil. 2)the meso-nonlinear features of soil sample are studied quantitatively which embody the meso-mechanism of the strength and deformation about cement-soil.

Key words:cement-soil; actual meso-model; digital image processing; numerical simulation

中图分类号:TU43

文献标志码:A

DOI:10.3969/j.issn.1000-2375.2016.02.011

文章编号:1000-2375(2016)02-0148-05

作者简介:王伟(1976-)，男，副教授，E-mail: wwei@njit.edu.cn

基金项目:南京工程学院创新基金(CKJB201310)和南京工程学院青年学术骨干教师基金资助

收稿日期:2015-06-30