一类Monge-Ampère方程Neumann问题的梯度估计

向妮,吴燕,石菊花

(湖北大学数学与统计学学院,应用数学湖北省重点实验室,湖北 武汉 430062)



一类Monge-Ampère方程Neumann问题的梯度估计

向妮,吴燕,石菊花

(湖北大学数学与统计学学院,应用数学湖北省重点实验室,湖北 武汉 430062)

摘要：将文献[1]中的方法运用到一类Monge-Ampère方程det[D2u-σ(x,u)]=f(x,u,Du)的Neumann边值问题中,分别得到梯度内估计,近边梯度估计以及边界梯度估计,从而得到退化椭圆解的全局梯度估计.

关键词：Monge-Ampère方程;Neumann边值条件;退化椭圆解的梯度估计

0引言

我们研究一类Monge-Ampère方程:

det[D2u-σ(x,u)]=f(x,u,Du),在Ω内

(0.1)

满足如下Neumann边值条件

Dγu=φ(x,u),在∂Ω上

(0.2)

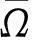
在文献[2]中,Lions等研究了如下Monge-Ampère方程

detD2u=f(x,u,Du),在Ω内

(0.3)

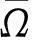
在文献[4]中,李松鹰研究了复Monge-Ampère方程的多重下调和解的适定性问题:

(0.4)

满足Neumann边值条件:Dvu=φ(z,u),在∂Ω上

(0.5)

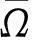
其中σ:Ω×R→H是C上所有n×nHermitian矩阵的集合.当fu和fpl满足如下结构性条件时:

fu≥0,在∂Ω上，

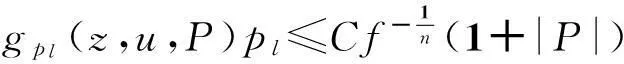
其中g=logf和P=(p1,p2,…,pn),通过构造闸函数将整体约化到边界,在边界上分方向讨论了解的梯度估计与二阶导数估计.

下面,我们给出这篇文章的主要结论:

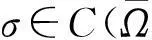
(0.6)

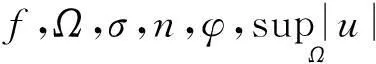
本文中由以下几部分构成:第一部分,我们介绍了椭圆解的定义,后面证明所需的记号以及梯度内估计;第二部分,我们得到整体梯度估计,并给出定理的证明.

1预备知识

这一章,我们将给出基本的记号,以及后面证明所需的定义和定理.

设Ω是Rn中有界区域,n≥2,∂Ω∈C3,γ是∂Ω上的单位内法向量.令

d(x)=dist(x,∂Ω)

(1.1)

和

Ωμ={x∈Ω:d(x)<μ}

(1.2)

|Dγ|+|D2γ|≤C(n,Ω),在Ωμ1内

(1.3)

(1.4)

引入记号:

cij=δij-γiγj,在Ωμ1内

(1.5)

(1.6)

下面,我们给出退化椭圆解的定义.

定义1.1我们称解u∈C2(Ω)是方程(0.1)式的退化椭圆解,若增广的Hessian矩阵是半正定的,即D2u-σ(x,u)≥0.

本文中,我们不能将Chou和Wang在文献[5]中的梯度内估计直接应用于这类型的Monge-Ampère方程(0.1)式.采用文献[5]中辅助函数的技巧,我们得到方程(0.1)的梯度内估计.

下面我们给出梯度内估计的证明.由于在文献[2]中,最大模估计已做讨论,在此我们可以假设u是有界的.

(1.7)

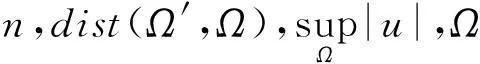
引理1.1的证明我们利用反证法来证明梯度内估计.不失一般性,我们假设Ω=B,其中r>0.∀Ω′⊂⊂Ω,令

(1.8)

通过计算可得,在x0点处,

(1.9)

(1.10)

(1.11)

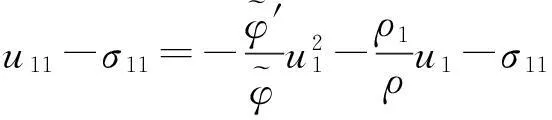
(1.12)

(1.13)

因此,

(1.14)

假设在x0处有下面的式子成立,

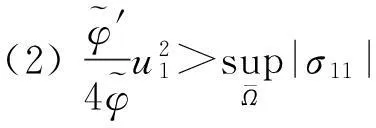
在x0点处,直接计算可得

以上可知,若有

(1.15)

式(1.15)与u是退化椭圆解矛盾.

因此,我们有

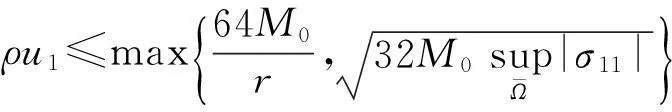
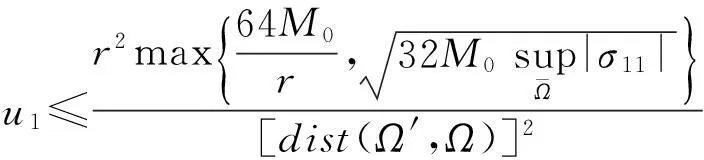
因此

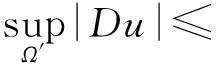
从而,我们得到引理1.1的证明.

2全局梯度估计

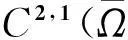
下面我们给出定理的证明.

定理的证明考虑如下函数

(2.1)

w(x)=u(x)-φ(x,u)d(x)

(2.2)

其中α0是一个待定的正数.

令

ψ(x)=logΨ(x)=log|Dw|2+h(u)+g(d)

(2.3)

其中h(u)=-log(1+4M0-u),g(d)=α0d.

假设ψ(x)的最大值在x0点处取得.

情形1.x0∈∂Ω.

对(2.3)式关于γ方向求导可得

(2.4)

由在∂Ω上d=0,可得wi=ui-Diφd-φγi=ui-φγi,wki=uki-Dkφγi-φDkγi

对(2.2)式关于法向γ求导,因为Dd=γ,则有wγ=uγ-φγd-φ=uγ-φ=0

(2.7)

由边值条件(0.2)式可得最后一个等式成立.

因此,在∂Ω上有,

(2.8)

因为

cklγl=(δkl-γkγl)γl=γk-γk=0

(2.9)

因此,

(2.10)

由(2.8)可知第一个等式成立,由(1.6)可知第二个等式成立,(2.5)式和(2.6)式可使得第3个等式成立,利用(2.9)可知第5个等式成立,由(1.3)和(1.4)可得第7个等式成立.

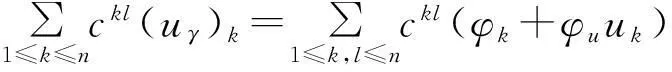
(2.11)

因此,

(2.12)

综合(2.10)式可得

(2.13)

将(2.13)式代入(2.4)式可得

(2.14)

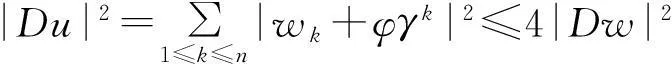
(2.15)

将(2.15)式代入(2.14)式可知,

(2.16)

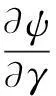
因此,

|Du(x)|≤C,在∂Ω上

(2.17)

情形2.x0∈Ωμ0,对于很小的μ0>0.

选取合适的坐标系使得

计算可得,

ui=wi+φγi+φid+φuuid

(2.18)

因此,

(1-φud)ui=wi+φγi+φid

(2.19)

(2.20)

类似地,可以得到

|Dw|2≤C2|Du|2

(2.21)

因为ψ(x)的最大值在x0点处取得,因此ψi(x0)=0,由(2.4)式可得

(|Dw|2)i=-|Dw|2(g′γi+h′ui)

(2.22)

由w1(x0)=|Dw|可知，

对i=1,结合(2.23)式和(2.25)式,可得

(2.26)

对φd求导可得(φd)1=φ1d+φuu1d+φγ1

(2.27)

(2.28)

将(2.26)式代入(2.28)式可得

(2.29)

因此,

φ11d+2φ1γ1+φ(γ1)1-(1-φud)σ11(x,u)

(2.30)

因为w1=u1-φ1d-φudu1=(1-φud)u1-φ1d,可得

(2.31)

因此,我们有

(2.32)

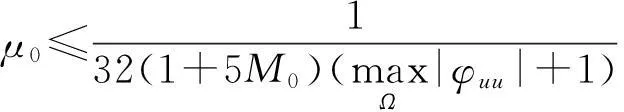
(2.33)

(2.34)

我们可假设下面的不等式成立,否则可得到结论

(2.35)

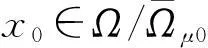
因此,综合上面3种情况我们得到梯度内估计,近边梯度估计以及边界梯度估计,从而得到了退化椭圆解的全局梯度估计.

3参考文献

[1] Xu J J. Gradient estimates for the Neumann problem of mean curvature equation[D]. Hefei: University of Science and Technology of China, 2014.

[2] Lions P L, Trudinger N S, Urbas J. The Neumann problem for problems of Monge-Ampère type[J]. Comm Pure Appl Math,1986(39): 539-563.

[3] Urbas J. On the second boundary value problem for equations of Monge-Ampère type[J]. J Reine Angew Math, 1997,487:115-124.

[4] Li S Y. Boundary value problems of complex Monge-Ampère type and applications[D].Pittsburgh: University of Pittsburgh, 1992.

[5] Gilbarg D, Trudinger N S. Elliptic partial differential equaqion of second order[M]. Berlin: Springer, 2001.

[6] Caffarelli L. The regularity of mappings with a convex potential[J]. J Amer Math Soc, 1992(5): 99-104.

[7] Caffarelli L. Boundary regularity of maps with convex potentials[J]. Comm Pure Appl Math, 1992,45: 1141-1151.

[8] Caffarelli L. Boundary regularity of maps with convex potencials Ⅱ[J]. Annals Math,1994, 144: 453-496.

[9] Jiang F D, Trudinger N S,Yang X P. on the Dirichlet problem for Monge-Ampère type equations[J].Cal Var Part Diff Eqns,2014,(49): 1223-1236.

[10] Li S Y. On the Neumann problems for complex Monge-Ampère equations[J]. Indiana Univ Math J,1994, 43: 1099-1122.

[11] Loeper G. On the regularity of solutions of optimal transportation problems[J]. Acta Math,2009(202): 241-283.

[12] Ma X N, Trudinger N S, Wang X J. Regularlity of potential functions of the optimal transportation problem[J]. Arch Rat Meth Anal , 2005,171: 151-183.

[13] Simon L M. Interior gradient bounds for non-uniformly elliptic equations[J]. Indians Univ Math J, 1976, 25: 821-855.

[14] Trudinger N S. Recent developments in elliptic partial differential equations of Monge-Ampère type[J]. Proc Int Cong Math, Madrid, 2006(3): 291-302.

[15] Trudinger N S，Wang X J. The Monge-Ampère equation and its geometric applications[J]. Handbook of Geometric Analysis, International Press, 2008(Ⅰ): 467-524.

[16] Trudinger N S，Wang X J. On the second boundary value problem for Monge-Ampère type equations and optimal transportation[J]. Ann Scuola Norm Sup Pisa Cl Sci, 2009 (Ⅷ): 143-174.

[17] Urbas J. Oblique boundary value problems for equations of Monge-Ampère type[J]. Calc Var Part Diff Eqns, 1998(7): 19-39.

[18] Vallani C. Optimal Transport-Old and new[M]. Berlin, Grundlehren: Springer, 2008.

[19] Wang X J. Oblique derivative problems for the equations of Monge-Ampère type[J]. Chinese J Contemp Math, 1992(13): 13-22.

[20] Chou K S, Wang X J. A variational theory of the Hessian equation[J]. Comm Part Diff Eqns, 2001,LIV: 1029-1064.

(责任编辑赵燕)

The gradient estimates for general Monge-Ampèreequations for Neumann problem

XIANG Ni1, WU Yan2, SHI Juhua3

(Hubei Key Laboratory of Applied Mathematics,Faculty of Mathematics and Statistics,Hubei University,Wuhan 430062,China)

Abstract:We extend the method in [1] to general Monge-Ampère equations det[D2u-σ(x,u)]=f(x,u,Du) with the Neumann boundary value condition, and get the interior gradient estimates, near the boundary gradient estimates and boundary gradient estimates respectively, then we obtain global gradient estimates of the degenerate elliptic solution.

Key words:general Monge-Ampère equations; the Neumann boundary value condition; gradient estimates of the degenerate elliptic solution

中图分类号:O175.25

文献标志码:A

DOI:10.3969/j.issn.1000-2375.2016.02.012

文章编号:1000-2375(2016)02-0153-07

作者简介:向妮(1981-),女,博士，副教授；吴燕,通信作者,E-mail：18827363287@163.com

基金项目:国家自然科学基金(11101132),湖北省教育厅科学技术研究项目(Q20120105)和创新思维导向的微分方程课程开放式实践教学体系的研究项目资助

收稿日期:2015-07-25