钢筋混凝土圆形单柱桥墩粒子群延性抗震优化
田英侠,王 超
(西安工业大学 建筑工程学院,西安 710021)
钢筋混凝土圆形单柱桥墩粒子群延性抗震优化
田英侠,王 超
(西安工业大学 建筑工程学院,西安 710021)
为了优化钢筋混凝土桥墩结构抗震设计,采用粒子群优化算法和反应谱分析方法,以截面特性和配筋率为设计变量,以抗震需求能力比为目标函数,建立了规则桥梁圆形单柱桥墩的抗震优化设计框架.计算结果表明:设计优化后与原设计相比,截面半径增加9.28%,纵向钢筋配筋率和横向箍筋配筋率分别增加7.76%和11.63%时,抗弯轴力、抗弯弯矩、抗剪及位移延性需求能力比分别降低了10.96%,9.15%,3.39%和29.92%;该方法实现了多目标需求最优设计参数的快速获取.
桥墩;粒子群;反应谱;抗震需求能力
墩柱的损伤破坏是桥梁震害的主要形式,一个墩柱的损伤可导致其丧失承受竖向荷载的能力,故墩柱失效常常是桥梁倒塌的主要原因[1].汶川地震中,映秀镇附近的百花大桥,都江堰附近的庙子坪大桥和高原大桥,彭州附近的小鱼洞大桥均是由于桥墩延性不足而引起桥梁的整体破坏[2-3].国内外相关研究表明[4-6]:墩柱轴压比、纵向钢筋配筋率、纵向钢筋等级、横向钢筋配箍率、横向钢筋等级、混凝土的强度等级、混凝土配合比和保护层厚度等因素将直接影响桥墩的延性水平.
文献[7]采用改进的遗传算法以悬索桥塔墩材料用量为目标函数,以强度、位移、整体稳定及抗倾覆等4个约束条件,对悬索桥塔墩体系抗震优化设计.文献[8]采用遗传算法以截面半径、纵向钢筋配筋率和横向箍筋配筋率为设计变量,以结构的初始材料造价、抗震强度需求能力比、抗震延性需求能力比为优化目标函数,建立圆形单柱桥墩的优化设计方法,能较好地平衡抗震设计的各种关键因素.文献[9]采用遗传算法建立了圆形单柱钢筋混凝土桥墩的地震损伤全寿命周期的和抗震性能方面的优化设计框架,为桥墩抗震优化设计提供了新方法.但由于桥墩设计复杂,应用遗传算法,迭代次数过多,计算缓慢且易收敛至局部最优点.而粒子群优化算法具有计算速度快、鲁棒性强及不受函数形式限制,并避免收敛至局部最优点[10]的特点.基于此文中将粒子群优化算法引入桥墩结构抗震设计中,结合反应谱法,以延性、抗剪性能为目标,建立普通规则桥梁圆形单墩数学计算模型,为桥墩抗震优化设计提供参考.
1 基于反应谱法延性抗震设计
对于普通圆形单墩规则且单跨跨径小于150 m的桥梁,从反应谱法出发,可将单墩简化为单自由度计算模型[11].由此,桥墩延性设计模型被简化为一个单自由度杆件.
1.1 E1地震作用下桥墩的设计
《公路桥梁抗震设计细则》(JTG/T B02-01-2008)[12]中对于水平方向作用力,采用阻尼比为0.05的加速度反应谱S为
(1)
式中:Tg为特征周期;T为结构自振周期;Smax为水平设计加速度反应谱的最大值.
在规则桥梁的柱式墩中,支座顶面处水平地震力Ehtp为
Ehtp=Sh1Gt/g
(2)
式中:Sh1为相应水平方向的加速度反应谱值;Gt为支座顶面处的换算质点重力;g为重力加速度.
墩柱的轴力设计值Nd、弯矩设计值Md,则可按一般偏心受压构件来验算其强度,其计算为
γoNd≤Nu=Ar2fcd+Cρr2fsd′
γoMd≤Mu=Br2fcd+Dρgor3fsd′
(3)
式中:γo为桥梁结构重要性系数;Nu、Mu分别为正截面抗压承载力和抗弯承载力;A、B为有关混凝土承载力的计算系数;C、D为有关纵向钢筋承载力的计算系数;r为桥墩截面半径;ρ为纵向钢筋配筋率;go为纵向钢筋所在圆周的半径和截面半径的比值;fcd、fsd′为混凝土轴心抗压强度设计值和普通钢筋抗压强度设计值.
得到以截面半径r和纵向钢筋配筋率ρ为设计变量,以轴力和弯矩的抗震能力为目标函数的计算框架.
1.2 E2地震作用下桥墩的设计
桥梁延性抗震设计就是通过合理的配置墩底的箍筋,在地震时由墩底产生的塑性铰的来抵抗和耗散地震作用力.假定规则桥梁的单柱形圆墩仅在墩底产生塑性铰,并且墩顶的位移延性需求满足
Δd≤Δu
(4)
式中:Δd为在E2地震作用下墩顶的位移;Δu为桥墩容许位移.
利用反应谱法,可以计算出墩顶位移Δd,而相应的Δu为
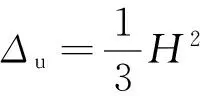
(5)
式中:φu为极限曲率;φy为屈服曲率;LP为等效塑性铰长度;K为延性安全系数;H为桥墩高度.
塑性铰区还应满足抗剪需求验算
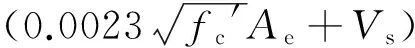
(6)
式中:Vd为剪力设计值;Vu为桥墩塑性区的斜截面抗剪承载力;φ为抗剪强度折减系数;fc′为混凝土抗压强度标准值;Ae为核心混凝土面积;Vs为箍筋提供的抗剪能力.
由此可建立以截面半径r和横向钢筋配筋率ρl为设计变量的桥墩延性位移和抗剪能力的计算框架.
2 桥墩抗震设计的粒子群优化算法计算框架
2.1 粒子群优化算法
粒子群算法是通过个体间的协作和竞争实现全局搜索的一种仿生学算法[13].算法的实现是通过鸟群在觅食过程中,互相传递信息,在得到别人信息的基础上并加上自己的判断,不断调整自己在整个种群中的位置和自身飞行速度,从而整个种群在食物附近聚集.重复以上的过程相当于人工促使生物种群进化,在种群进化的每代之中,个体都不断通过自我学习和社会学习[14]不断调整自己在种群中的速度和位置,这样的过程就是不断发展并得到全局最优解的过程.
在粒子群优化算法中,搜索空间的每一个点都代表这目标函数的一个解,称此点为粒子.粒子在搜索空间内以某一初速度飞行,并根据自我学习和社会学习得到的经验来不断指导自己搜索轨迹,不断更新位置和速度,在个体最优位置pbest和整体最优位置gbest中不断迭代,以完成整个搜索.位置更新和速度更新为
(7)

2.2 桥墩优化计算模型
选定对设计影响较大的3个参数,即截面半径r、纵向钢筋配筋率ρ和横向箍筋配筋率ρl为设计变量,得到桥墩设计变量
X=[r,ρ,ρl]T
(8)
纵向钢筋配筋率对桥墩设计的影响较大,其取值范围为0.006~0.04.
最小横向钢筋配箍率为
ρl,min=[0.14ηk+5.84(ηk-1)(ρ-0.1)+ 0.028]fc′/fyh≥0.004
(9)
式中:ηk为轴压比;ρ为纵向钢筋配筋率;fyh为箍筋抗拉强度设计值.
普通规则圆形单墩的优化设计变量边界约束条件为
(10)
在优化过程中,将能力与需求联系起来,可以分别得到E1地震作用下抗弯轴力需求能力比Δ1和抗弯弯矩需求能力比Δ2,E2地震作用下抗剪能力需求能力比Δ3和延性位移需求能力比Δ4四个目标函数为
Δ1=Nd/Nu,Δ2=Md/Mu,
Δ3=Vd/Vu,Δ4=Δd/Δu
(11)
2.3 桥墩结构的优化流程
桥墩结构粒子群优化算法的计算流程如下:①根据桥墩结构的截面半径、纵向钢筋配筋率和横向钢筋配筋率为设计背景,在搜索空间中随机产生初始种群,其中包含了初始速度、初始位置、学习因子和算法终止条件的相关参数;②根据4个不同的目标函数,即:抗弯轴力需求能力比Δ1和抗弯弯矩需求能力比Δ2,抗剪能力需求能力比Δ3和延性位移需求能力比Δ4,对每一个粒子,评价优化函数的适用值;③更新种群中每个个体最优值pbest和整个种群的全局最优值gbest;④按照粒子的速度和位置的计算式(7)来计算粒子的速度和位置,以便及时调整位置和速度; ⑤根据终止条件的适用规则,判断是否满足终止条件,如果满足条件则转至下一步计算;否则转至③,继续循环计算; ⑥算法运行结束,输出桥墩优化计算结果.
应用粒子群算法和反应谱法建立规则桥梁圆形单墩的计算框架,给出了优化设计的程序.
3 优化结果分析
某一中等规格C类桥梁,所处地区场地类别为Ⅰ类,地震峰值加速度0.15 g,特征周期0.4 s,在两阶段设计中抗震重要性系数分别为0.34和1.0,水平地震反应谱场地系数0.9,阻尼调整系数0.3,圆形单柱墩墩高10 m,跨径40 m,上部结构重量200 kN·m-1,纵筋采用HRB335型钢筋,箍筋采用HRB235型钢筋,C40等级商品混凝土[15].
图1为4个目标函数应用粒子群算法的计算结果.在图1(a),1(b)分别为在横向地震力E1作用下,以截面半径和纵向钢筋配筋率为设计变量的抗弯轴力、抗弯弯矩需求能力比的收敛曲线;图1(c),1(d)分别为横向地震力E2作用下,以截面半径和横向钢筋配筋率为设计变量的抗剪能力和位移延性需求比.由图1中可以看出,4个目标函数均在第10代以内收敛,迭代速度快.在E1地震作用下,截面半径r为1 m,纵向钢筋配筋率ρ为0.012 5,相应的抗弯轴力需求能力比Δ1为0.060 5,抗弯弯矩需求能力比Δ2为0.056 6;在E2地震作用下,截面半径r仍为 1 m,横向钢筋配箍率ρl为0.004 8,相应的抗剪能力需求比Δ3为0.418 8,位移延性需求能力比Δ4为0.018 5.
比较文中优化设计结果与文献[15]的设计结果,见表1.
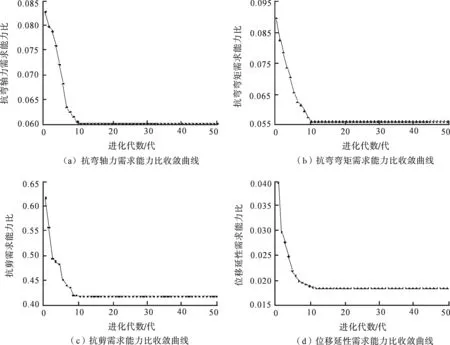
图1 圆形单墩优化结果Fig.1 Optimization results of single circular pier
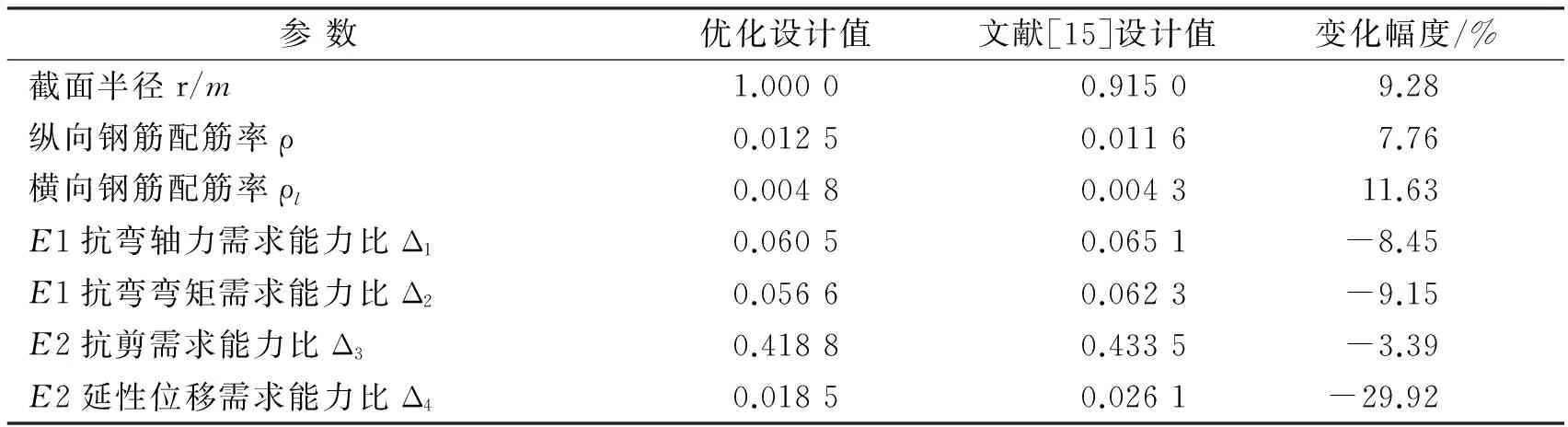
参数优化设计值文献[15]设计值变化幅度/%截面半径r/m1.00000.91509.28纵向钢筋配筋率ρ0.01250.01167.76横向钢筋配筋率ρl0.00480.004311.63E1抗弯轴力需求能力比Δ10.06050.0651-8.45E1抗弯弯矩需求能力比Δ20.05660.0623-9.15E2抗剪需求能力比Δ30.41880.4335-3.39E2延性位移需求能力比Δ40.01850.0261-29.92
相较于文献[15]设计值,优化后截面半径增加了9.28%,纵向钢筋配筋率增加了7.76%,横向钢筋配筋率增加了11.63%,抗弯轴力需求能力比降低了10.96%,抗弯弯矩需求能力比降低了9.15%,抗剪需求能力比降低了3.39%,延性位移需求能力比降低了29.92%.抗震结构优化后使材料用量有所增加,桥墩的抗震性能提高,更符合设计意图.
4 结 论
1) 将粒子群优化算法和反应谱方法结合起来,以抗弯轴力需求能力比、抗弯弯矩需求能力比、抗剪能力需求能力比和位移延性需求能力比为目标函数,提出了规则桥梁圆形单墩的抗震优化设计方法.该方法采用粒子群算法搜索同时满足局部和整体的最优解,快速获得满足多目标需求的桥墩最优设计参数.
2) 算例优化结果表明,截面半径增加9.28%时,纵向钢筋配筋率增加7.76%,横向钢筋配筋率增加11.63%,抗弯轴力需求能力比降低了10.96%,抗弯弯矩需求能力比降低了9.15%,抗剪需求能力比降低了3.39%,位移延性需求能力比降低了29.92%,桥墩的抗震性能得以提高.
3) 该方法为地震作用下钢筋混凝土规则桥梁圆形单墩抗震设计提供了新思路,使得设计者从以设计经验为主的被动校核转为以设计目标为主的主动设计,减轻了设计工作量.
[1] 马建,孙守增,杨琦,等,中国桥梁工程学术研究综述[J].中国公路学报,2014,27(5):1.
MA Jian,SUN Shouzeng,YANG Qi,et al.Review on China’s Bridge Engineering Research[J].China Journal of Highway and Transport,2014,27(5):1. (in Chinese)
[2] 杜修力,韩强,李忠献,等.5.12汶川地震中山区公路桥梁震害及启示[J].北京工业大学学报,2008,34(12):1270.
DU Xiuli,HAN Qiang,LI Zhongxian,et al.The Seismic Damage of Bridges in the 2008 Wenchuan Earthquake and Lessons From Its Damage[J].Journal of Beijing University of Technology,2008,34(12):1270.(in Chinese)
[3] 雷涛,李碧雄,曹鹏杰,等.汶川地震近断层附近桥梁震害浅析[J].重庆交通大学学报(自然科学版),2010,29(3):358.
LEI Tao,LI Bixiong,CAO Pengjie,et al.Analysis on Damage of Near-Faultage Bridges in Wenchuan Earthquake[J].Journal of Chongqing Jiaotong University(Natural Science),2010,29(3):358. (in Chinese)
[4] 冯清海,袁万城.混凝土桥墩塑性铰区箍筋用量RBFNN改进算法[J].哈尔滨工业大学学报,2008,40(10):1629.
FENG Qinghai,YUAN Wancheng.An Improved Calculation Method for Stirrup Ratios in Plastic Hinge Regions of Concrete Piers by Using RBF Neural Network[J].Journal of Harbin Institute of Technology,2008,40(10):1629.(in Chinese)
[5] 孙治国.钢筋混凝土桥墩抗震变形能力的研究[D].哈尔滨:中国地震局工程力学研究所,2012.
SUN Zhiguo.Research on the Seismic Deformation Capacity of RC Bridge Columns[D].Harbin:Institute of Engineering Mechanics,China Earthquake Administration,2012.(in Chinese)
[6] HAN Qiang,DU Xiuli,LIU Jingbo,et al.Seismic Damage of Highway Bridges During the 2008 Wenchuan Earthquake[J].Earthquake Engineering and Engineering Vibration,2009,8(2):263.
[7] 谢楠,陈英俊.遗传算法的改进策略及其在桥梁抗震优化设计中的应用效果[J].工程力学,2000,17(3):31.
XIE Nan,CHEN Yingjun.Improving Strategies on Genetic Algorithm and Its Application to the Optimum Design of Bridges under Earthquake[J].Engineering Mechanics,2000,17(3):31.(in Chinese)
[8] 郑玉国,袁万城.基于GA-RS的规则钢筋混凝土桥梁圆形单柱桥梁延性抗震优化设计[J].振动与冲击,2010,29(3):81.
ZHENG Yuguo,YUAN Wancheng.Optimal Ductile Seismic Design of Regular RC Single-column Circular Bridge Piers Based on GA-RS[J].Journal of Vibration and Shock,2010,29(3):81.(in Chinese)
[9] 柳春光,张士博,柳英洲.基于NSGA-II的规则桥梁圆形单柱RC桥墩全寿命造价优化设计[J].水利与建筑工程学报,2015,13(2):1.
LIU Chunguang,ZHANG Shibo,LIU Yingzhou.NSGA-II Optimization on Life Cycle Seismic Design of Single Circular Reinforced Concrete Bridge Piers[J].Journal of Water Resources and Architectural Engineering,2015,13(2):1.(in Chinese)
[10] LI M W,KANG H G,ZHOU P F,et al.Hybrid Optimization Algorithm Based on Chaos,Cloud and Particle Swarm Optimization Algorithm[J].Journal of Systems Engineering and Electronics,2013,24(2):324.
[11] YE Jihong,ZHANG Zhiqiang,LIU Xianming.A Simplified Multisupport Response Spectrum Method[J].Earthquake Engineering and Engineering Vibration,2012,11(2):243.
[12] 重庆交通科研设计院.公路桥梁抗震设计细则:JTG/T B02-01-2008[S].北京:人民交通出版社,2008.
Chongqing Communications Research and Design Institute.Guidelines for Seismic Design of Highway Bridges:JTG/T B02-01-2008[S].Beijing:China Communications Press,2008.(in Chinese)
[13] ZHAO J,ZHOU R.Particle Swarm Optimization Applied to Hypersonic Reentry Trajectories[J].Chinese Journal of Aeronautics,2015,28(3):822.
[14] WANG Y Y,ZHANG B Q,CHEN Y C.Robust Airfoil Optimization Based on Improved Particle Swarm Optimization Method[J].Applied Mathematics and Mechanics,2011,32(10):1245.
[15] 普瑞斯特雷 M J N,赛勃勒 F,卡尔维 G M.桥梁抗震设计与加固[M].袁万城,译.北京:人民交通出版社,1997.
PRIESTRAY M J N,SAIBOLE F,CALVI G M.Seismic Design and Reinforcement of Bridge[M].YUAN Wancheng,Transl.Beijing:China Communications Press,1997.(in Chinese)
(责任编辑、校对 张 超)
Ductility Seismic Optimization of Reinforced Concrete Single Circular Bridge Pier Based on Particle Swarm
TIANYingxia,WANGChao
(School of Civil Engineering,Xi’an Technological University,Xi’an 710021,China)
To optimize the reinforced concrete pier structure design,particle swarm optimization algorithm and response spectrum method were combined to build a seismic design optimization framework of regular single circular bridge pier.The optimization adopted cross-section characteristic and reinforcement ratios as variables and seismic demand ability ratios as objective functions.The calculation indicated:Compared with the original design,the demand ability ratio of anti-bending axial force,anti-bending moment,anti-shear and displacement ductility decreased 10.96%,9.15%,3.39% and 29.92% respectively as the radius,longitudinal and transverse reinforcement ratio increased 9.28%,7.76% and 11.63% respectively;The proposed design achieved the optimum parameters to meet the multi-objective needs quickly.
bridge pier;particle swarm;response spectrum;seismic demand ability
10.16185/j.jxatu.edu.cn.2016.12.005
2016-03-26
西安工业大学校长基金项目(XAGDXJJ14021)
田英侠(1974-),女,西安工业大学副教授,主要研究方向为结构抗震.E-mail:tianyingxia@126.com.
U443.22
A
1673-9965(2016)12-0970-06

