集中质量对模拟测头基频的影响

强怀博,吴 琼

(1.西安工业大学 机电工程学院,西安 710021；2.西安建筑科技大学 机电工程学院,西安 710055)

集中质量对模拟测头基频的影响

强怀博1,吴 琼2

(1.西安工业大学 机电工程学院,西安 710021；2.西安建筑科技大学 机电工程学院,西安 710055)

为了改善三维模拟测头的响应特性及其动态稳定性,对三维模拟测头进行了基频分析.将模拟测头的各主要组成部件简化为集中质量模型,采用模态分析方法分析了工作基频对响应特性及测量精度的影响.通过集中质量分布位置及其影响敏度分析,结果表明：集中质量及其位置对于测头系统基频的影响呈非线性关系.以集中质量为约束条件的频率响应特性分析可有效提高模拟测头动态性能及测量精度,为提高模拟测头测量精度及动态性能提供了新途径.

集中质量；基频；模拟测头；非线性

在精密测量领域中,测头精度一直是制约测量系统总体精度的重要环节.由于接触式三维模拟测头具有测量精度高、效率高等优点,故在精密测量领域中被广泛应用.对于接触式三维模拟测头系统,为了能够有效提高测量精度,改善测头工作时的动态稳定性及其响应特性,需要在动态性能研究中对其进行基频分析,将模拟测头中的导向机构、驱动机构、传感单元和测量力平衡装置等部分简化为集中质量模型,采用模态分析方法研究测量基频对测量精度的影响.

在此领域的研究中,文献[1]提出将不确定质量用区间向量进行定量化,提出基于区间数学理论的预测弹簧质量系统频率与质量的非概率分析方法.文献[2-3]通过对电感测微仪测头运动模型的建立,对接触式动态测量时测头与工件的临界脱离频率进行了分析,提出增加测头的刚度和预压量，减小测头活动部分的质量,采用密度较小的材料,以提高测头的动态响应性能.文献[4]根据欧拉-伯努利方程,建立测头导向机构的伪刚体动力学模型,并结合算例对不同模型的系统频率进行比较分析.在求解过程中需关注集中质量所引起测头基频的变化.故需研究测头基频和模态之间的关系,有研究结果表明测头基频和模态之间近似呈线性关系[5-6],但这种推算的依据值得商榷.本文将三维模拟测头的主要组成部件简化为集中质量模型,采用模态分析方法研究工作基频对响应特性的影响,并进行集中质量分布位置及其影响敏度的研究,通过试验验证理论分析的正确性.

1 集中质量与测头的基频的关系

高精度三维模拟测头属于接触式测量仪器,三维测头的结构如图1所示.

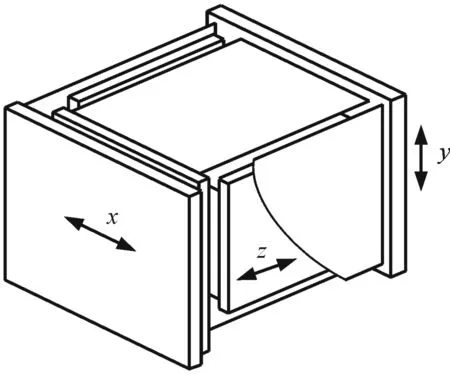
图1 三维测头的结构简图Fig.1 Structure of 3D analog probe

图1中x，y，z为测量坐标.测头工作机构的运动是通过平行簧片导向机构实现,导向机构是测头的关键部分,其他机构的布置都与导向机构有一定的联系[4].故在研究过程中,以导向机构为基础,将其抽象为如图2所示的等截面的Euler-Bernoulli模型,在该模型中导向机构的平行簧片是由柔性薄板制成,P为导向簧片上某一点,F(x,θ)为作用在P点的作用力,θ为P点在F(x,θ)下的转角.设测头的测量力F(x)、截面惯性矩I(x)和弹性模量E(x)均为x向位置的函数.此外,将模拟测头内的驱动机构、传感单元和平衡装置等机构的载荷假设为集中质量.

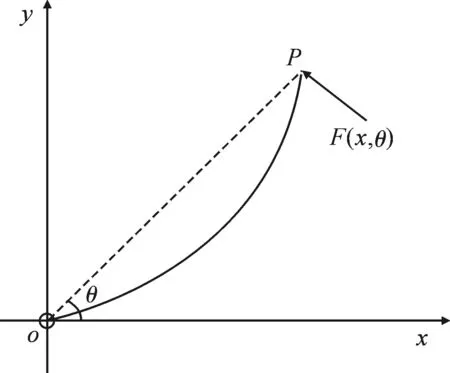
图2 等截面的Euler-Bernoulli模型

在研究模拟测头工作过程中的共振问题时,考虑模拟测头系统处于有阻尼状态,即系统阻尼ζ≠0,由模拟测头的动态性能研究[4]可知,测头强迫振动的Euler-Bernoulli微分方程为

(1)

式中：θ为导向板的摆角；Y(x,θ)为导向板的挠度；ρ为导向板的密度.

分析测头导向机构的工作基频时,可采用Lanczos法或矢量迭代法,但是由于其影响因素较多,研究模型较为复杂[7-8].当不需要定量计算而只需理论上定性分析时,就可以参考图2所示模型,用Rayleigh迭代法来研究模拟测头的基频与动态参数的关系,即

(2)

式中：Y(x)为不考虑导向板摆角的挠度；mi为测头第i个单元的集中质量；ω为测头的基频；γ为簧片中性面长度；n为测头集中质量的单元数.

将式(2)改写为

(3)

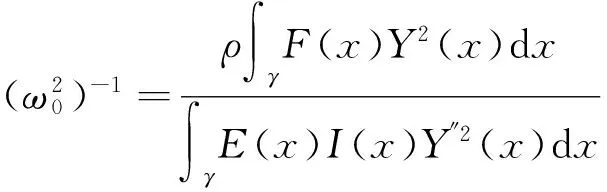
(4)

i=(1,2,…,n)

(5)

式中：Y(xi)为第i个集中质量所对应的挠度；ω0为不存在集中质量，仅考虑导向板自身载荷作用下测头的基频；ωi为不考虑导向板的分布载荷作用，仅在第i个集中质量作用下的测头基频.

通过式(2)和式(3)可以得到,模拟测头中各集中质量对测头基频的影响是非线性的,集中质量对测量基频的影响不仅取决于各个集中质量的大小,还取决于载荷的分布位置.

将式(3)改写为

(6)

将式(6)对ωi求偏导,研究各集中质量对模拟测头基频的影响,即

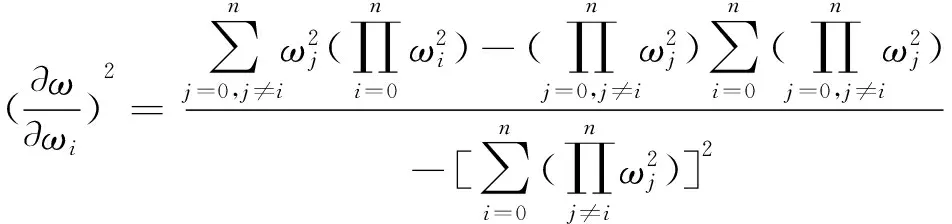
(7)

其中ωj为不考虑导向板的分布载荷作用,仅在第j个集中质量作用下的测头基频.

由式(7)还可得,即使测头集中质量的大小相同,由于布局位置不同也会对测量基频产生不同的影响.

2 基频影响敏度分析

为了清楚地说明分析方法且简化研究过程,设在模拟测头某一坐标导向系统内套装有传驱动机构、传感单元和测量力平衡装置,则可将式(3)展开,可得

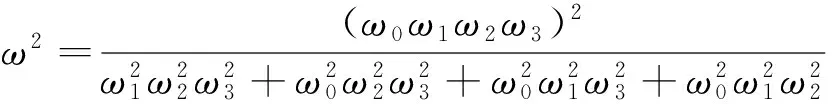
(8)

则有

(9)

(10)

(11)

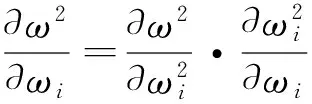
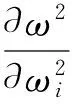
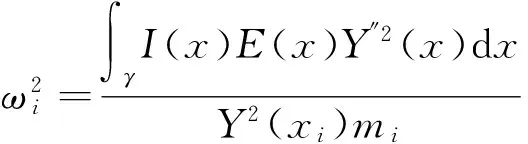
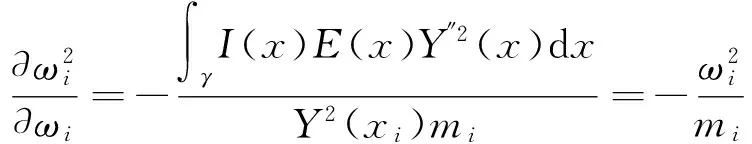
(12)

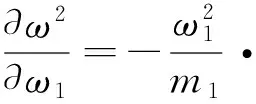
(13)

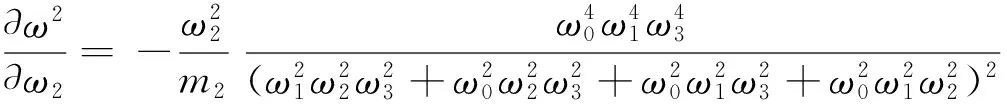
(14)

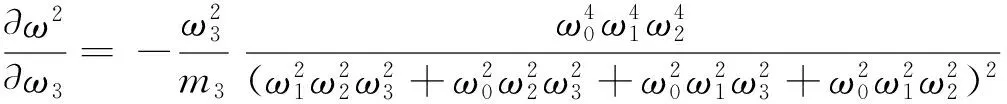
(15)

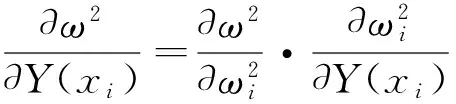
(16)

可见测头上各单元的集中质量对于测量基频影响呈非线性关系,而且集中质量的分布位置对基频的影响也是呈非线性的,由于基频公式较为复杂性，影响因素较多,且计算结果的精度很难满足工程要求[5].试验模态分析是通过测量实际系统的激励和响应信号来实现模态参数的识别.本文将采用试验模态分析方法建立测头系统的基频模型,以获得测头结构动态参数的精确性.

3 实验分析

为了验证集中质量及其位置对测头基频的影响,以高精度模拟测头为研究对象进行试验,一维模拟测头的导向机构由均质柔性平行簧片薄板制成,采用四点固定方式,材料为QBe2,其弹性模量为126GPa,泊松比为0.3.测头基频分析测试系统主要由激励源、检测单元、数据采集系统、计算分析软件和计算机等部分组成,检测单元选用CAYD108型压电式加速度传感器,频率测量范围为0.5～5 000Hz,灵敏度为100pC·g-1,放置于导向簧片的中间位置,搭建实验数据和激励信号采集电路.

应用有限元法进行模态分析,表1给出不同集中质量对测头基频的影响.随着集中质量的增加,测头工作基频呈减小趋势,势必带来测头动态性能变差.因此要提高测头的工作基频,理论上就应该减小测头集中质量的大小.

根据试验得出一维测头在3种不同集中质量作用下的频率响应曲线如图3所示.由图3可以看出，集中质量对测头基频的影响是呈非线性变化.驱动单元m1、传感单元m2和平衡装置m3对测头工作基频的影响呈现相同趋势的变化,而且驱动单元对测头工作基频的影响较为明显,这是因为驱动单元作用力直接影响到测头与被测工件之间的接触效果,其受到外界干扰、振动等因素影响较大,可见改善测头驱动单元的影响可以有效改善测头的动态工作性能.

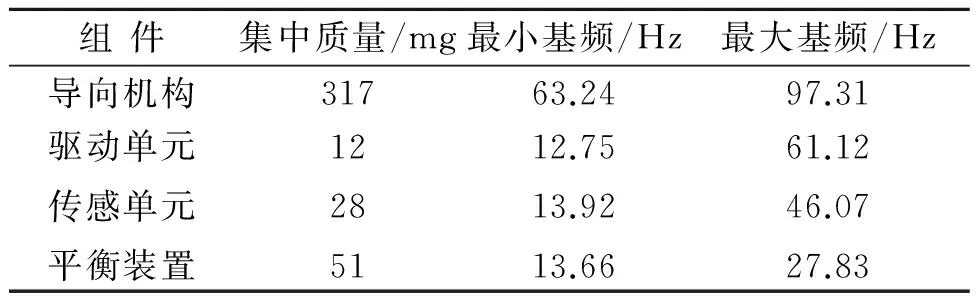
表1 不同集中质量对测头基频的影响

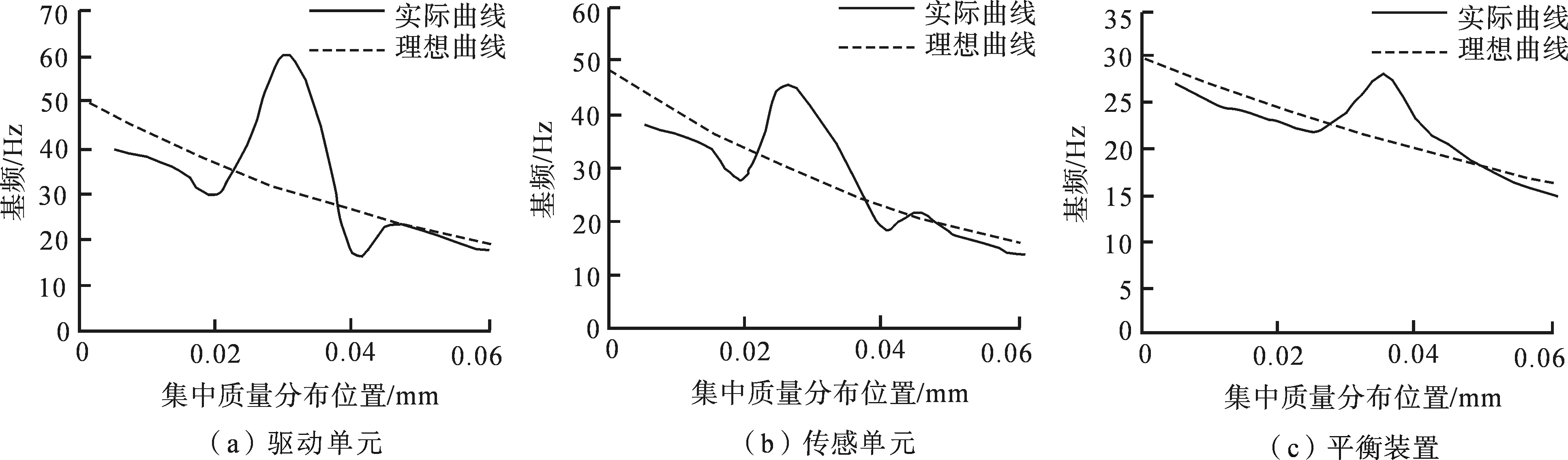
图3 不同集中质量作用下一维测头的频率响应曲线

4 结 论

本文应用有限元法对模拟测头导向机构进行模态分析,通过动态分析基频和集中质量关系,得到结论为

1) 集中质量对测头基频的影响与集中质量的大小及分布位置有关.集中质量与测头工作基频不存在线性关系.驱动单元、传感单元和平衡装置对测头工作基频的影响曲线呈相同变化趋势,且驱动单元对测头工作基频的影响更为明显.

2) 在结构设计过程中,通过以集中质量为条件的频率响应特性分析可有效提高模拟测头的动态性能及测量精度.在模拟测头的动态性能分析过程中,模拟测头的简化集中质量模型误差需进行进一步研究.

[1] LYON S M,ERICKSON P A,EVANS M S,et al.Prediction of the First Modal Frequency of Compliant Mechanisms Using the Pseudo-Rigid-Body Model[J].Journal of Mechanical Design,1999,121(2):309.

[2] 李平,王建华,李晓丽,等.影响测微仪测头临界脱离频率因素的研究[J].机床与液压,2006(10):149.

LI Ping,WANG Jianhua,LI Xiaoli,et al.Study on Factors of Influencing Inductive Probe Critical Frequency[J].Machine Tool & Hydraulics,2006(10):149.(in Chinese)

[3] 李平,王建华,来跃深,等.测微仪测头临界脱离频率的研究[J].工具技术,2004,38(12):62.

LI Ping,WANG Jianhua,LAI Yueshen,et al.Study on Critical Frequency of Inductive Probe[J].Tool Engineering,2004,38(12):62.(in Chinese)

[4] 强怀博,王建华,吴琼.基于柔性铰链结构的三维模拟测头设计[J].现代电子技术,2007,30(1):102.

QIANG Huaibo,WANG Jianhua,WU Qiong.A Design of Three Dimensional Analog Probe Based on Flexure Hinges[J].Modern Electronics Technique,2007,30(1):102.(in Chinese)

[5] 牟新明,王建华,杨密.平行簧片机构力学分析与计算[J].纳米技术与精密工程,2005,3(4):278.

MU Xinming,WANG Jianhua,YANG Mi.Mechanical Analysis and Computation of Parallel Springs[J].Nanotechnology and Precision Engineering,2005,3(4):278.(in Chinese)

[6] 李海燕,张宪民,彭惠青.大变形柔顺机构的驱动特性研究[J].机械科学与技术,2004,23(9):1040.

LI Haiyan,ZHANG Xianmin,PENG Huiqing.Research on the Actuation Characteristic of a Large-Deflection Compliant Mechanism[J].Mechanical Science and Technology,2004,23(9):1040.(in Chinese)

[7] SAXENA A,ANANTHASURESH G K.On an Optimal Property of Compliant Topologies[J].Structural & Multidisciplinary Optimization,2000,19(1):36.

[8] ELMUSTAFA A,LAGALLY M G.Flexural-Hinge Guided Motion Nanopositioner Stage for Precision Machining:Finite Element Simulations[J].Precision Engineering,2001,25(1):77.

(责任编辑、校对 潘秋岑)

【相关参考文献链接】

强怀博,吴琼.模拟测头导向机构动力学特性研究[J].2010,30(2)：130.

李花妮,路俊勇.GB-KKT-不变凸非线性优化问题[J].2015,35(5)：352.

雷志勇,王娇,王泽民.电容法的工业酒精浓度测量及其非线性修正[J].2014,34(11)：891.

陈以田.轴向运动屈曲梁非线性振动研究[J].2014,34(4)：280.

强怀博,吴琼.线切割工艺参数优化的非线性回归模型[J].2011,31(7)：621.

王志,吴红芳.基于非线性自适应观测器的飞机操纵面故障诊断[J].2011,31(3)：267.

王林艳,李蔚,王党利,等.非线性机械故障诊断的核分布粒子滤波方法[J].2010,30(5)：433.

毕红梅.求解一类非线性隐式变分不等式的神经网络[J].2010,30(1)：83.

顾致平,于渊博,高永刚,等.一种非线性弹性支承转子系统的非线性特性研究[J].2009,29(4)：375.

路畅,李立钢.基于Bezier曲线的透视投影非线性放大方法研究[J].2007,27(2)：162.

倪晋平,陈亚林,马时亮.非线性LMS算法实现盲源分离[J].2006,26(5)：413.

马娜蕊.连续时间非线性时滞系统的新最优控制算法[J].2006,26(3)：280.

王春玲,任学敏.均质场地非线性地震反应的半解析算法[J].2005,25(3)：266.

Influence of Basic Frequency of Concentrated Mass to Analog Probe

QIANGHuaibo1,WUQiong2

(1.School of Mechatronic Engineering,Xi’an Technological University,Xi’an 710021,China; 2.School of Mechanical Engineering,Xi’an University of Architecture and Technology,Xi’an 710055,China)

In order to improve the response and stability of 3D analog probe,the fundamental frequency of the probe was analyzed.The main components of 3D analog probe were simplified as concentrated mass model,the effect of basic frequency on response characteristic and measurement accuracy was analyzed. Focusing on the analyzing the distribution and influence sensitivity of concentrated mass,the results indicate that it is non-linear relationship between basic frequency and mass location of probe.The frequency response characteristics are analyzed to utilize concentrated mass as constraint condition,which is an effective means to improve the dynamic performance and measurement accuracy.

concentrated mass;basic frequency;analogue probe;nonlinearity

10.16185/j.jxatu.edu.cn.2016.12.004

2016-08-28

陕西省教育厅重点实验室科研计划项目(2015JS043)

强怀博(1979-),男,西安工业大学讲师,主要研究方向为精密加工与测量技术.E-mail:qianghuaibo@126.com.

TP216

A

1673-9965(2016)12-0965-05