无人驾驶车辆路径跟踪的增量式PID控制
谭宝成,王 宾
(西安工业大学 电子信息工程学院,西安 710021)
无人驾驶车辆路径跟踪的增量式PID控制
谭宝成,王 宾
(西安工业大学 电子信息工程学院,西安 710021)
为了实现无人驾驶车辆沿着预设路径安全稳定行驶,基于车辆实际位置和给定位置的坐标关系,建立了无人驾驶车辆的路径跟踪模型;分析车辆当前位置及航向信息与目标路径的偏差,提出误差带内外分状况的控制策略;通过改进和优化传统增量式比例积分微分控制(PID控制)算法,提出了一种新型增量式PID控制算法.实验结果表明:改进后的增量式PID算法相较于传统增量式PID算法,无人车路径跟踪的上升时间、调整时间均减小,响应速度加快,超调量减小,车辆实现快速稳定的路径跟踪.
无人驾驶车辆;路径跟踪;PID控制;误差带
路径跟踪是无人车研究方向的一项关键技术.路径跟踪控制算法是指能够使无人车按照预设路径,安全稳定行驶的控制方法.较早的路径跟踪方法,如几何路径规划法[1-2]、滚动路径法等[3],比较适用于室内机器人;但由于无人车是非完整约束,车体大,受到转弯半径、角速度等的约束,对于无人车是不适用的.文献[4-5]采用Backsteping积分法,设计出系统跟踪控制器,但该控制器的设计较为简单,对复杂环境的适应性较差.文献[6]将运动学控制器的输出作为动态控制器的输入,但缺乏通过控制信息的输出反馈两者有机的联系.多数研究运用模糊控制算法对车辆的路径跟踪进行控制[7-9],这种算法得到的反馈信号存在滞后,滞环等特性,很难使车辆行驶在目标路径上.文献[10]提出了自适应模糊控制器方法,但由于模糊控制规则数目是系统变量个数的指数函数,因此模糊规则条数过多反而影响了其应用.多种控制方式考虑到了实际因素和扰动对系统的影响,提出了鲁棒控制法[11-12],进行了仿真试验,但理论结果和实际情况存在较大偏差.将理论上的控制方法应用到实际工程中去,实验验证准确无误后才应用到实际工程中.本文在车辆航向和位置控制上,对传统的增量式比例积分微分(ProportionalIntegralPlusDerivative,PID)控制方法进行优化,在航向反馈控制中,根据偏差值调整微分作用和积分作用的强弱,以达到较好的控制效果,并具有较强的适应性.
1 无人车路径跟踪模型建立
无人车路径跟踪数学模型如图1所示,在大地直角坐标系中,假设预设路径上有A、B、C三个相邻的预设点,坐标分别为(xg1,yg1)、(xg2,yg2)、(xg3,yg3),预设点上的航向分别为hg1、hg2、hg3.某一时刻,通过全球定位系统(Global Positioning System,GPS)获取无人车在大地直角坐标系中的当前位置为D(xF,yF),行驶的航向为hF[13].
假设当前无人车正行驶于A,B两点之间,
B点是车辆的目标点.已知A,B两点坐标,可求得通过A,B两点的直线方程[14]为
ax+by+c=0
(1)
其中a=(yg2-yg1),b=(xg1-xg2),
c=-a·xg1-b·yg1
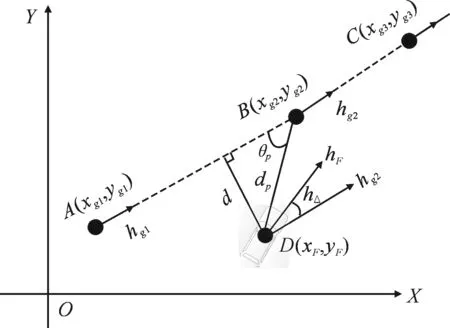
图1 无人车路径跟踪数学模型Fig.1 Mathematical model of unmanned vehicle path tracking
根据无人车当前位置坐标及AB直线方程,求得当前车辆到AB直线的垂直距离为
(2)
无人车和目标点(点B)之间的直线距离为
(3)
无人车和目标点所在直线与给定路径直线AB夹角θp的余弦为
(4)
无人车的实际航向与目标航向差为
hΔ=hF-hg2
(5)
2 路径跟踪控制策略
2.1 误差带范围内的控制策略
本实验设定允许误差带范围为0.2 m.将无人车看作一个质点,在车辆行驶过程中的任一时刻,当测得车辆当前位置与给定路径的垂直距离小于0.2 m时,则车辆所处位置在允许的误差范围内,如图2所示.此时,按照PID算法精确控制车辆行驶航向,且按照给定航向行驶.误差带内控制策略如图3所示.图3中ek为航向给定量和反馈量的差值.

图2 车辆处于误差带内示意图Fig.2 The schematic diagram of vehicle inside the error band
2.2 误差带范围外的控制策略
在车辆行驶过程中,若测得车辆当前位置与给定路径的垂直距离d≥0.2 m,则车辆所处位置超出误差带范围,暂时性偏离给定路径,如图4所示.此时,应调整PID控制器输入值,期望PID控制器输出值使得车辆向靠近给定路径的一侧行驶.因此,PID控制器的输入值应调整为给定航向与反馈航向差值再减去一个给定的角度调整值.误差带外控制策略如图5所示.此角度调整值的作用就在于当车辆行驶至误差带范围外时,使得PID控制器的输入量发生变化,进而调整输出,使得车辆向靠近给定路径的一侧行驶.若无此角度调整值,当车辆行驶至误差带范围外时,还采用原来的控制方法,结果必然是在误差带范围外,车辆按照给定的航向行驶.航向满足要求,但无人车位置并没有满足要求,即没有按照给定的路径行驶,没能实现准确的路径跟踪.故而,此角度调整值对于路径跟踪影响显著.

图3 误差带内控制策略Fig.3 Control strategy for inside the error band

图4 误差带外控制策略Fig.4 Control strategy for out of the error band
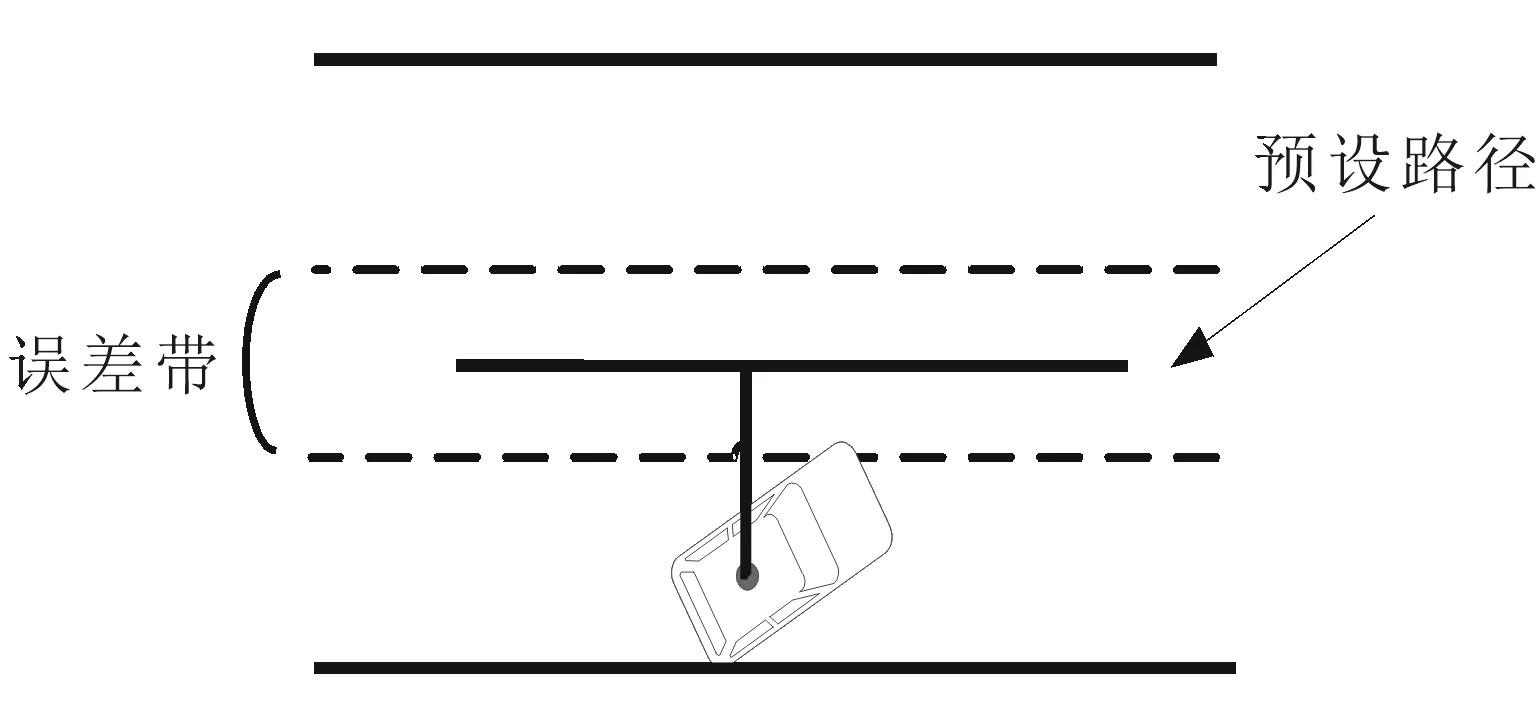
图5 车辆处于误差带外示意图Fig.5 Schematic diagram of vehicle out of the error band
3 改进增量式PID控制器的设计
离散化增量式PID控制律为
Δu=Aek+Bek-1+Cek-2
(6)
(7)
式中:ek为控制器的输出;ek-1,ek-2均为给定量和反馈量的差值;KP为比例系数;TI,TD分别为积分时间和微分时间;T为采样周期.PID控制器的参数不能跟随环境的改变而变化.当这种传统算法应用在高精度航向控制上会产生较大的超调.
在PID算法中引入积分环节的主要目的是为了减小系统静差,提高系统的控制精度,对于积分项的改进,本文采取积分分离法.当PID控制器的输入量ek的绝对值 大于某一正临界值|ek|时,此时,采取PD控制,令积分项系数KI=0,此时,积分项无作用.而当|ek|≤ε时,此时,采取PID控制,积分项系数KI≠0,根据系统特性可确定KI的取值.TI为积分时间,KI和TI为倒数关系,即KI=1/TI.
微分系数的引入主要是为了改善闭环系统的稳定性和动态响应速度,这是由于微分系数主要影响系统误差变化速率.微分系数过大,就会使阻尼过大,导致系统调节时间过长.减小微分系数时,系统响应变得迟钝和缓慢,动态特性变差.Δe2为偏差变化量平方值.当Δe2较大时,微分项系数较小,微分作用弱.而当Δe2较小时,微分项系数较大,微分作用强[15].
采用阶梯式微分系数自整定法来改进微分项.具体做法是将Δe2分成若干段,每段对应不同的值,即每段对应不同微分项系数,每一段内系数固定不变.当然分段的段数和分段的宽度可进行调整,每一段的系数可先设定,执行程序时,查取微分系数.设微分系数为KD,KD=TD,TD为微分时间.设定下限值为L,设定上限值为H,当Δe2≤L时,KD=1;当Δe2≥H时,KD=0.当L<Δe2 图6 微分系数分段示意图Fig.6 Differential coefficient segment schematic 由于PID控制器的输出是控制车辆方向盘的转角,车辆方向的改变不会瞬时变化太大.因此对PID控制器采取输出限幅措施,使得控制器输出量Δu保持在某一范围内.设输出上限幅为YH,下限幅为YL.限幅律表达式为 (8) 其中Δui为限幅输出. 根据以上所述的控制方法,可以得到控制算法步骤如下:① 计算ek.读取给定值 rk、反馈值ck,角度调整值δ,读取车辆当前位置到预设路径的距离,判断车辆是否在误差带内.若在误差带内, ek=rk-ck;反之,ek=rk-ck-δ.② 确定积分系数.判断ek的大小,若|ek|≤ε,KI等于设定值;反之,KI=0.③ 确定微分系数.定义误差变动量的平方值为Δe2=(ek-ek-1)2,判断Δe2的大小,若Δe2小于下限值L,KD=1;若Δe2大于上限值H,KD=0;若Δe2处于两者之间,KD的计算由微分系数分段函数确定.④ 计算控制器输出值Δu.由KP,KI,KD,根据式(6)、式(7)计算Δu.⑤ 根据式(8)确定限幅输出Δui. 为了验证改进型PID控制器的优越性,试车实验分两组进行验证,第1组取传统增量式PID控制器.设定比例系数、积分系数和微分系数分别为KP=0.2、KI=1.67和KD=0.4,采样周期T=0.2.第2组实验采用改进后的PID控制器,参数设定如下:设定比例系数KP=0.2;ε=15°.|ek|>15°时,KI=0;|ek|<15°时,KI=1.67.微分系数分段为5段,参数设置见表1.PID控制器输出设定上限幅为10°,下限幅为-10°,即方向盘转角每次最多变化10°.两组实验均设定智能车的初始航向为35°,即正北偏东35°,计算机记录车辆的航向变化,并绘制出PID控制响应曲线如图7所示. 表1 微分系数分段表Tab.1 Differential coefficient segment table 注:Δe为误差变动量. 从图7可以看出,改进后的PID控制算法使得系统的上升时间、调整时间均缩短,响应速度加快.即当给定航向发生变化时,车辆能够更加快速地调整输出,跟随给定航向. 相对于传统的PID控制算法,改进后的PID控制算法使得系统的超调量减小.即车辆航向不出现过大的偏差,在路径跟踪实验中,车辆可稳定地沿预设路径行驶. 图7 PID控制响应曲线图Fig.7 PID control response curve 1) 基于车辆实际位置和给定位置,提出了无人车路径跟踪数学模型.该模型通过计算车辆当前位置及航向的几何位置关系,得到了无人车与目标点所在直线和预设路径的夹角以及无人车实际航向与目标航向差. 2) 无人车行驶当前位置与给定路径的垂直距离小于允许误差带范围时,车辆处于误差带内,车辆航向控制策略为增量式PID控制.车辆处于误差带外,增量式PID控制器的输入为给定航向与反馈航向角度差的校正值. 综上所述,初中数学的课前预习是有效学习的必要步骤。培养学生的良好预习习惯,不仅符合新课程发展要求,对于学生的知识学习也具有良好的前后衔接作用,能够有效激发学生的学习兴趣,促使学生主动学习和探究,增加学生发现问题的机会,培养学生主动学习习惯。因此,在实际教学中,教师应采取多样化的方式,加大对课前预习的重视,有效激发学生的数学预习兴趣,加强对学生预习的检查和指导,促使学生养成良好的数学预习习惯,提高学习效率。 3) 无人车改进增量式PID控制算法相对于传统增量式PID算法,路径跟踪系统的上升时间、调整时间均较小,响应速度较快,超调量减小. [1] 刘亚杰,王航宇,谢君.狭窄环境中基于几何法的全局路径规划新方法[J].海军工程大学学报,2010,22(4):82. LIU Yajie,WANG Hangyu,XIE Jun.A New Global Path Planning Method Based on Geometry Algorithm in a Narrow Environment[J].Journal of Naval University of Engineering,2010,22(4):82.(in Chinese) [2] 周之平,黎明,华路.基于几何相交测试的机器人路径规划算法[J].控制与决策,2011,26(11):1695. ZHOU Zhiping,LI Ming,HUA Lu.Geometry Intersection Testing Based Robot Path Planning Algorithm[J].Control and Decision ,2011,26(11):1695. (in Chinese) [3] 张纯刚,席裕庚.机器人滚动路径规划的算法与仿真研究[J].高技术通讯,2003,13(4):53. ZHANG Chungang,XI Yugeng.Algorithm and Simulation of Robot Rolling Path Planning[J].High Technology Letters,2003,13(4):53.(in Chinese) [4] 徐俊艳,张培仁.非完整轮式移动机器人轨迹跟踪控制研究[J].中国科学技术大学学报,2004,34(3):376. XU Junyan,ZHANG Peiren.Research on Trajectory Tracking Control of Nonholonomic Wheeled Mobile Robots[J].Journal of University of Science and Technology of China,2004,34(3):376.(in Chinese) [5] 郭一军,段杏林,赵磊.基于BackSteping算法的工业机械臂快速精确跟踪控制器设计[J].天津理工大学学报,2015,31(5):21. GUO Yijun,DUAN Xinglin,ZHAO Lei.The Design of a Fast and Accurate Industrial Manipulator Tracking Controller Based on Back Stepping Algorithm[J].Journal of Tianjin University of Technology,2015,31(5):21.(in Chinese) [6] WU J,XU G,YIN Z.Robust Adaptive Control for a Nonholonomic Mobile Robot with Unknown Parameters[J].Control Theory and Technology,2009,7(2):212. [7] KIM J,ZHANG F,EGERSTEDT M.Curve Tracking Control for Autonomous Vehicles with Rigidly Mounted Range Sensors[J].Journal of Intelligent & Robotic Systems,2009,56(1):177. [8] 熊波,曲仕茹.基于模糊控制的智能车辆自主行驶方法研究[J].交通运输系统工程与信息,2010,10(2):70. XIONG Bo,QU Shiru.Intelligent Vehicle's Path Tracking Based on Fuzzy Control[J].Journal of Transportation Systems Engineering and Information Technology,2010,10(2):70.(in Chinese) [9] 林焕新,胡跃明,陈安.基于自适应模糊控制的智能车控制系统研究[J].计算机测量与控制,2011,19(1):78. LIN Huanxin,HU Yueming,CHEN An.Research on Control System of Intelligent Car Based on Self-Adaptive Fuzzy Control[J].Computer Measurement & Control,2011,19(1):78.(in Chinese) [10] 佟绍成,周军.非线性模糊间接和直接自适应控制器的设计和稳定性分析[J].控制与决策,2000,15(3):293. TONG Shaocheng,ZHOU Jun.Design and Stability of Fuzzy Indirectand Direct Adptive Control for Nonlinear System[J].Control and Desion,2000,15(3):293.(in Chinese) [11] 李旭,张为公,陈晓冰.无人驾驶车辆侧向鲁棒控制的研究[J].汽车工程,2004,26(6):730. LI Xu,ZHANG Weigong,CHEN Xiaobing.A Research on Lateral Robust Control Strategy for Intelligent Vehicle[J].Automotive Engineering,2004,26(6):730.(in Chinese) [12] 孟建军,李德仓,胥如迅,等.基于H∞鲁棒控制的无人驾驶城轨车辆运行姿态研究与仿真[J].兰州交通大学学报,2011,30(6):88. MENG Jianjun,LI Decang,XU Ruxun,et al.Simulation and Research on Running Attitude of Unmanned Urban Rail Vehicle Based on H∞Robust Control[J].Journal of Lanzhou Jiaotong University,2011,30(6):88.(in Chinese) [13] 谭宝成,邓子豪.车载导航系统精确定位算法的优化[J].西安电子科技大学学报(自然科学版),2014,41(3):181. TAN Baocheng,DENG Zihao.Vehicle Navigation System Optimization of Precise Positioning Algorithm[J].Journal of Xidian University(Natural Science),2014,41(3):181.(in Chinese) [14] TAN B,LV F.Position and Attitude Alternate of Path Tracking Heading Control[J].Sensors & Transducers,2014,167(3):203. [15] 李庆哲,梁秀满,刘振东,等.改进型增量式PID算法在S7-200中的程序实现[J].工业仪表与自动化装置,2013(6):29. LI Qingzhe,LIANG Xiuman,LIU Zhendong,et al.The Program Realized of Improved Incremental PID Algorithm in the S7-200[J].Industrial Instrumentation & Automation,2013(6):29.(in Chinese) (责任编辑、校对 张 超) 【相关参考文献链接】 张立广,谭宝成,马天力.无人驾驶车辆路径跟踪控制器的设计及实现[J].2013,33(8):680. 陈超波,胡莉,马颖,等.一种改进式遗传算法优化分数阶PID控制器[J].2016,36(6):510. 苗荣霞,王彬.啤酒发酵温度的参数自整定模糊PID控制[J].2016,36(2):167. 郭全民,雷蓓蓓.汽车磁流变半主动悬架的模糊PID控制研究[J].2015,35(3):192. 王昕炜,苗荣霞.锻造操作机大车行走机构的单神经元自适应PID控制[J].2014,34(12):1012. 谭宝成,马天力.无人车运动稳定性的模糊神经网络PID控制[J].2013,33(4):334. 秦刚,陈凯,高惠中,等.内模PID控制器在智能车转向系统中的应用及仿真[J].2011,31(7):649. 王航宇,倪原.基于卡尔曼滤波器的电动汽车PID控制系统设计[J].2008,28(3):267. 来跃深,司瑞强.专家PID控制器的CPLD设计[J].2007,27(5):421. 谭宝成,崔佳超.改进人工势场法在无人车避障中的应用[J].2014,34(12):1007. 谭宝成,曹康凯.人工势场法在无人车避障系统中的改进[J].2012,32(12):1020. 郝瑞卿,闫莉.军事配送式后勤车辆路径问题研究[J].2015,35(1):63. 谭宝成,廉春原,徐艾,等.一种基于改进遗传算法的机器人路径规划方法[J].2008,28(5):456. 国蓉,刘磊,孟祥众.圆柱零件加工用直线电机模糊自适应PID控制及建模[J].2015,35(12):968. 钟旭佳,高晓丁,严楠.电液比例压力控制系统的PID参数优化[J].2015,35(2):106. 李聚锋,倪原,刘智平,等.某飞行器舵机控制的模糊PID算法[J].2013,33(3):198. 谭宝成,康祖清.模糊PID算法在定型机温控系统上的应用[J].2012,32(11):895. 杨盛泉,刘白林,裴昌幸.灰色预测PID模型的建筑构件耐火试验炉控制系统[J].2012,32(4):315. 秦刚,王新茹.PID结构广义预测控制算法的仿真及分析[J].2012,32(2):162. 谭宝成,成法坤.自适应模糊PID在中频弯管机温度控制中的应用[J].2010,30(2):191. 王航宇,倪原.基于卡尔曼滤波器的电动汽车PID控制系统设计[J].2008,28(3):267. 樊泽明,冯卫星,王亮,等.智能阀门定位器PID单参数模糊自适应控制设计[J].2007,27(6):563. 高嵩,朱峰,肖秦琨,等.机载光电跟踪系统的模糊自整定PID控制[J].2007,27(4):312. Path Following Incremental PID Control for Unmanned Vehicle TANBaocheng,WANGBin (School of Electronic Information Engineering,Xi’an Technological University,Xi’an 710021,China) To make the unmanned vehicle follow the planned route with security and stability,based on the relationship between the actual position and the given position,path tracing model for unmanned vehicle is established.The deviation between actual position and the given course is analyzed.The different control strategies for inner or outer the error band is designed.By improving and optimizing the traditional incremental PID control algorithm, a novel PID algorithm is put forward.Test results show:The improved PID algorithm makes the rise time and the adjust time of path tracking system of unmanned vehicle shorter,response speed faster,overshoot volume decreased,and performance better,compared with the traditional incremental PID algorithm.The vehicle achieves fast and stable path tracking. unmanned vehicle;path tracing;PID control;error band 10.16185/j.jxatu.edu.cn.2016.12.009 2016-03-09 中央财政支持地方高校专项发展基金(CXY1080) 谭宝成(1955-),男,西安工业大学教授,主要研究方向为计算机控制系统、复杂控制系统和远程控制. E-mail:xaitdzx@163.com. TP273 A 1673-9965(2016)12-0996-06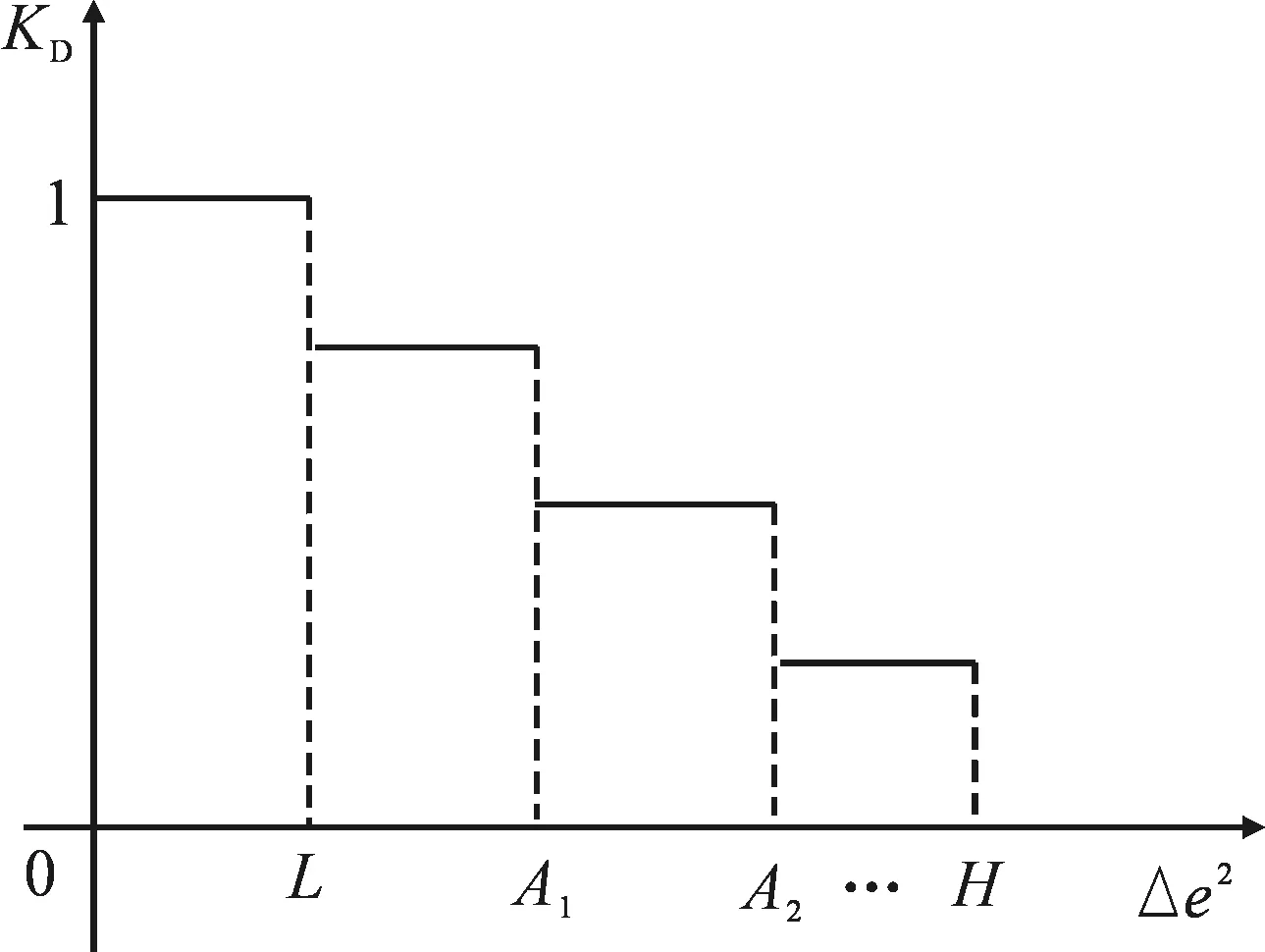
4 实验及分析

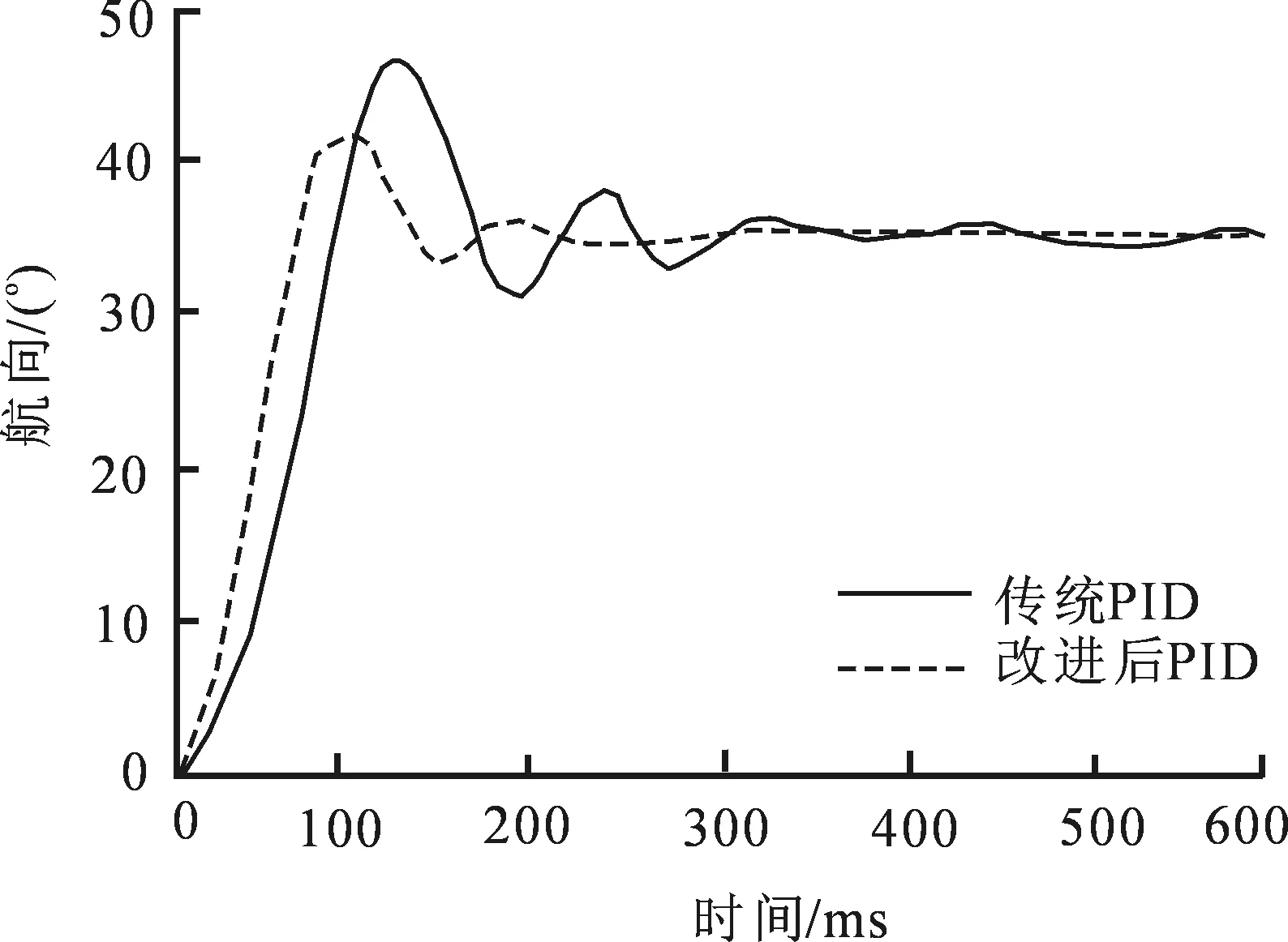
5 结 论

