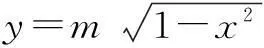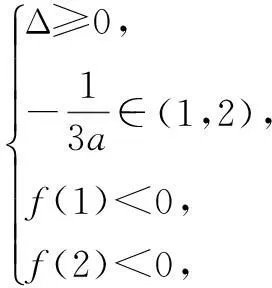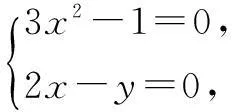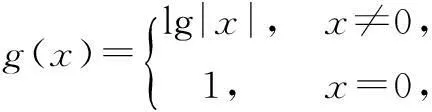零点问题中“以形助数”的若干要点



零点问题中“以形助数”的若干要点

陈俊峰

(江苏省天一中学,214101)

一、准确画图是前提

g(x)=f(x)+2k,若函数g(x)恰有两个不同的零点,则实数k的取值范围为______.

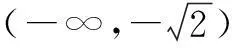
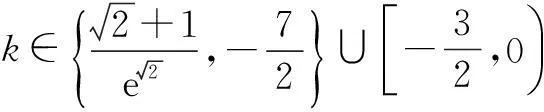
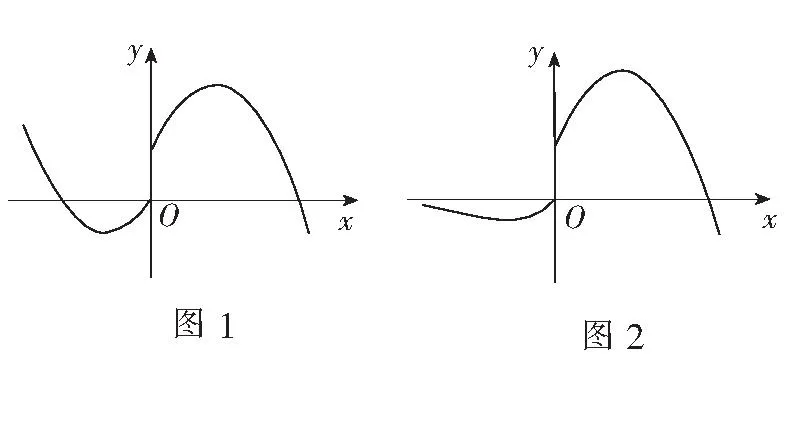
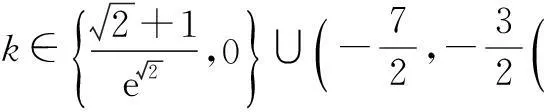
二、临界位置细分析

错解令t=x2+2x,则a=f(t),分别画出y=f(t)和y=x2+2x的图象(如图3、4).由图3可以得出,当2

分析错解对临界位置没有仔细分析推敲,由图4,只有当t>-1时,直线y=t和函数y=x2+2x的图象有两个不同的交点,所以在函数y=f(t)的图象上找出横坐标为-1的点,因为f(-1)=8,结合图5,所以实数a的取值范围为(8,9].

《组织学》是研究机体微细结构及其相关功能的科学。得利于显微镜的出现，这门科学将解剖学中的宏观（主要指系统和器官水平）结构推向了微观（主要指组织和细胞水平）。

三、通过变形求简化

四、转化等价是关键

例4若函数f(x)=lg(k+x)-lg(x-1)-lg(x-2)只有一个零点,则实数k的取值范围为______.

错解1令f(x)=0,则lg(k+x)=lg(x-1)+lg(x-2),所以k+x=(x-1)(x-2),即k=x2-4x+2,由Δ=0得k=-2.

错解2令f(x)=0,则lg(k+x)=lg(x-1)+lg(x-2)=lg[(x-1)(x-2)],由(x-1)(x-2)>0,解出x∈(-∞,1)∪(2,+∞).问题转化为函数y=k和y=x2-4x+2(x∈(-∞,1)∪(2,+∞))的图象只有一个公共点,结合图8,可解得k∈(-2,-1].

五、动定结合效率高

例5二次函数f(x)=3ax2+2x-a在区间(1,2)上有零点,则a的取值范围为______.

或f(1)f(2)<0，

当a>0时,同理,解出a无解.

注以上解法分类情况较多,而且容易出现遗漏,可进行如下优化.

六、代数论证可入微

错解画出函数f(x)和g(x)的图象,如图13.当x∈[-5,10]时,两图象在y轴左侧有4个公共点,在y轴右侧有9个公共点,加上点(0,1),所以两函数图象区间[-5,10]上公共点的个数一共为14个.