高三数学综合测试
高三数学综合测试
一、填空题(本大题共14小题,每小题5分,共70分)
1.若集合A={x|y=lg(2x-x2)},B={y|y=2x,x>0},则集合A∩B=______.
2.命题“∀x∈R,x2>0”的否定是______.
3.如果x-1+yi,与i-3x是共轭复数(x、y是实数),则x+y=______.

5.已知f(x)=-ax3+cx+2,若f(5)=7,则f(-5)=______.





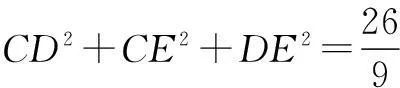
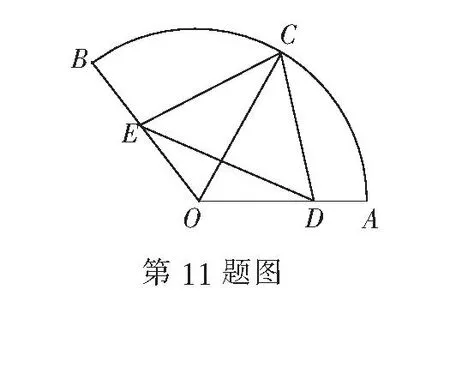
13.在f(x)定义是R上的奇函数,且当x≥0时,f(x)=x2.若对任意的x∈[a,a+2]均有f(x+a)≥2f(x),则实数a的取值范围为______.

二、解答题(本大题共6小题,共90分.解答时写出必要的文字说明、证明过程或演算步骤)
15.在∆ABC中,内角A,B,C的对边分别为a,b,c,若sin2B=sinAsinC.
(1)求ac-b2的值;

16.已知函数f(x)=x2-1,g(x)=a|x-1|,F(x)=f(x)-g(x).
(1)若a=2,x∈[0,3],求F(x)的值域;
(2)若a>2,解关于x的不等式F(x)≥0.
17.已知圆M:x2+(y-4)2=4,点P是直线l:x-2y=0上的一动点,过点P作圆M的切线PA、PB,切点为A、B.
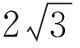
(2)若∆PAM的外接圆为圆N,试问:当P运动时,圆N是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由;
(3)求线段AB长度的最小值.
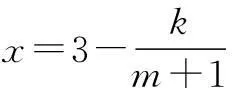
(1)将2016年该产品的利润y万元表示为年促销费用m万元的函数;
(2)该厂家2016年的促销费用投入多少万元时,厂家的利润最大?

(1)求椭圆的方程;
(2)求AB+CD的取值范围.

(1)当a=-2时,求函数f(x)的单调递减区间;
(2)设函数f(x)的导函数为f′(x),若存在唯一的实数x0,使得f(x0)=x0与f′(x0)=0同时成立,求实数b的取值范围;
(3)已知点A为曲线C上的动点,在点A处作曲线C的切线l1与曲线C交于另一点B,在点B处作曲线C的切线l2,设切线l1,l2的斜率分别为k1,k2.问:是否存在常数λ,使得k2=λk1?若存在,求出λ的值;若不存在,请说明理由.
三、附加题
2.某商场经销某商品,根据以往资料统计,顾客采用的付款期数ξ的分布列为:

ξ12345P0.40.20.20.10.1
商场经销一件该商品,采用1期付款,其利润为200元;分2期或3期付款,其利润为250元;分4期或5期付款,其利润为300元.η表示经销一件该商品的利润.
(1)求事件A:“购买该商品的3位顾客中,至少有1位采用1期付款”的概率P(A);
(2)求η的分布列及期望Eη.





(1)若a1(x),a2(x),a3(x)的系数依次成等差数列,求正整数n的值.
(2)求证:∀x1,x2∈[0,2],恒有
|F(x1)-F(x2)|≤2n-1(n+2)-1.
参考答案
一、填空题
1.(1,2);2.∃x∈R,x2≤0;

6.(x+1)2+y2=16;7.2;
二、解答题
15.(1)因为sin2B=sinAsinC, 由正弦定理,得b2=ac,所以ac-b2=0.

由余弦定理,得b2=a2+c2-2accosB,所以a2+c2=5.


当1≤x≤3时,x2-2x-1∈[0,4];
当0≤x<1时,x2+2x-3∈[-3,0);
所以F(x)=f(x)-g(x)的值域为[-3,4].
(2)F(x)=
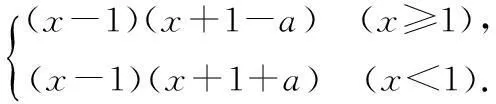
由x≥1,F(x)≥0,a>2,得x≤1或x≥a-1⟹x≥a-1或x=1;
由x<1,F(x)≥0,得x≤-a-1或x≥1⟹x≤-a-1.
综上,F(x)≥0⟹x≤-a-1或x≥a-1或x=1.


(2)设P(2b,b),因为∠MAP=90°,所以经过A、P、M三点的圆N以MP为直径,其方程为

即(2x+y-4)b-(x2+y2-4y)=0.
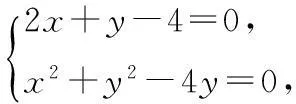

(3)因为圆N方程为

即x2+y2-2bx-(b+4)y+4b=0;
圆M:x2+(y-4)2=4,
即x2+y2-8y+12=0.
作差得圆M方程与圆N相交弦AB所在直线方程为2bx+(b-4)y+12-4b=0.

相交弦长即

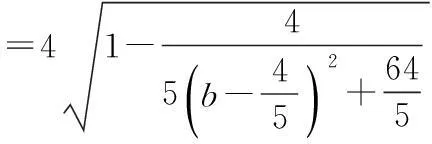

18.(1)由题意可知,当m=0时,x=1,∴1=3-k,即k=2.

∴2009年的利润
=4+8x-m
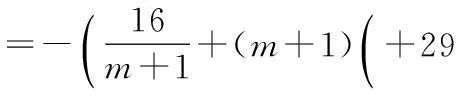


答:该厂家2016年的促销费用投入3万元时,厂家的利润最大,最大为21万元.
所以a2=4c2,b2=3c2.



(2)① 当两条弦中一条斜率为0时,另一条弦的斜率不存在,由题意知AB+CD=7.
② 当两弦斜率均存在且不为0时,设A(x1,y1),B(x2,y2),
且设直线AB的方程为y=k(x-1),

将直线AB的方程代入椭圆方程并整理,得
(3+4k2)x2-8k2x+4k2-12=0,

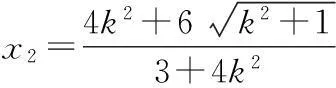




令t=k2+1,则t>1,3+4k2=4t-1,3k2+4=3t+1.
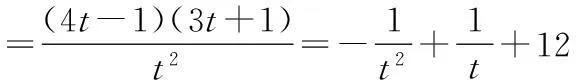
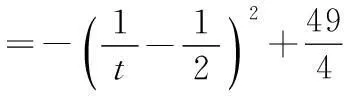




20.(1)当a=-2时,f′(x)=3x2+5x-2=(3x-1)(x+2).

(2)f′(x)=3x2+5x+a,由题意,知

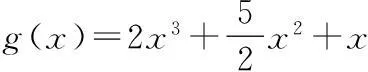
g′(x)=6x2+5x+1=(2x+1)(3x+1),

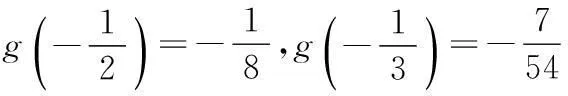
故实数b的取值范围是

(3)设A(x0,f(x0)),则点A处切线方程为
y-f(x0)=f′(x0)(x-x0).
与曲线C:y=f(x)联立方程组,得
f(x)-f(x0)=f′(x0)(x-x0),
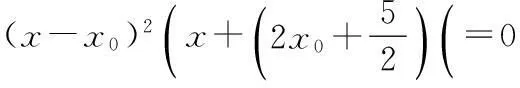
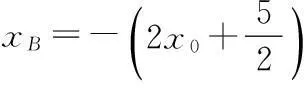
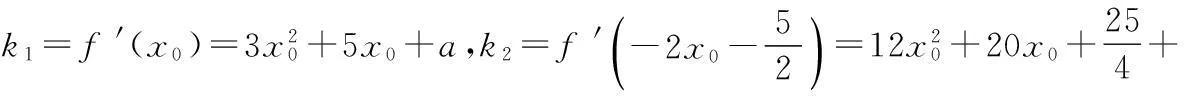
若存在常数λ,使得k2=λk1,则
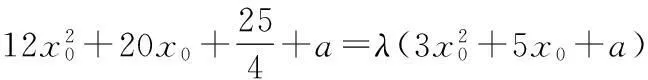
即存在常数λ,使得
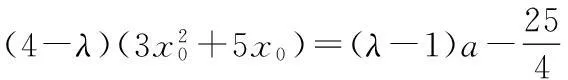


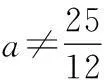
三、附加题
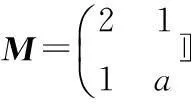

=(λ-2)(λ-a)-1=0,
则(3-2)(3-a)-1=0,解得a=2,

设直线x-2y-3=0上任一点(x,y)在M作用下对应的点为(x′,y′),则有


代入x-2y-3=0,整理得4x′-5y′-9=0,
∴所求直线方程为4x-5y-9=0.



(2)η的可能取值为200元,250元,300元.
P(η=200)=P(ξ=1)=0.4,
P(η=250)=P(ξ=2)+P(ξ=3)=0.2+0.2=0.4,
P(η=300)=1-P(η=200)-P(η=250)=1-0.4-0.4=0.2.
η的分布列为

η200250300P0.40.40.2
Eη=200×0.4+250×0.4+300×0.2=240(元).



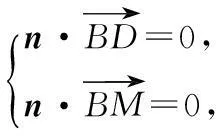
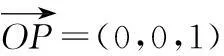


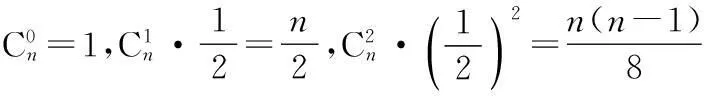


(2)F(x)=a1(x)+2a2(x)+3a3(x)+…
+nan(x)+(n+1)an+1(x)

令x=2,F(2)=C0n+2C1n+3C2n+…+nCn-1n+(n+1)Cnn.
令x=0,则F(0)=1.
设Sn=C0n+2C1n+3C2n+…+nCn-1n+(n+1)Cnn,则Sn=(n+1)Cnn+nCn-1n+…+3C2n+2C1n+C0n.考虑到Ckn=Cn-kn,将以上两式相加得2Sn=(n+2)(C0n+C1n+C2n+…+Cn-1n+Cnn),
∴Sn=(n+2)2n-1.
又当x∈[0,2]时,F′(x)≥0恒成立,从而F(x)是[0,2]上的单调增函数,
∴∀x1,x2∈[0,2],
|F(x1)-F(x2)|≤F(2)-F(0)
=2n-1(n+2)-1.
(2,3,1)则