小议圆锥曲线离心率取值范围问题
小议圆锥曲线离心率取值范围问题
潘建宁
(江苏省南京市人民中学,210008)
离心率是圆锥曲线的重要性质之一,离心率取值范围也是高考的热点.本文从几道例题入手,谈谈圆锥曲线离心率取值范围的常见题型和方法.
一、利用题目已知条件中存在的不等关系

评注如题目已知条件中出现不等关系,只需将其表示出来,再转化为离心率的取值范围即可.
二、利用图形中几何量的关系

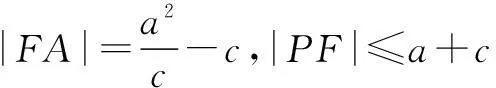
解法2设点P(x,y).由题意,|PF|=|FA|,由椭圆第二定义,有

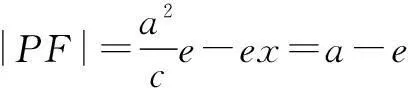
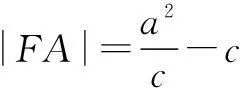

由于-a≤x≤a,

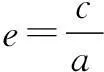
即(2e-1)(e+1)≥0.

例3若双曲线焦点在x轴上,过双曲线的右焦点F作实轴所在直线的垂线,交双曲线于A、B两点,设双曲线的左顶点为M.若点M在以AB为直径的圆的内部,则此双曲线的离心率e的取值范围是______.
以AB为直径的圆的方程为

又点M(-a,0)在圆的内部,所以有
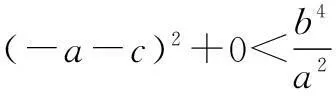

∴e2-e-2>0,解得e>2或e<-1.
又e>1,所以e∈(2,+∞).
评注解析几何体现了数与形的统一,题目图形中经常会出现一些几何关系,需从几何角度找到不等关系,再转化为离心率的取值范围.
三、利用焦半径的取值范围
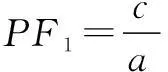
PF1-PF2=2a,
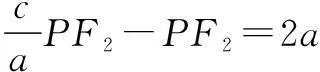
由焦半径的取值范围可知PF2>c-a,则

所以e2-2e-1<0,
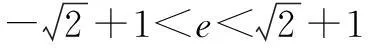

评注题目中如涉及焦半径计算,可先计算出焦半径,再通过圆锥曲线中焦半径的范围建立不等式求解.
四、利用圆锥曲线上点的坐标的取值范围
例5(同例4)
解由已知,得aPF1=cPF2,且点P在双曲线的右支上,设P点(x0,y0).
由焦点半径公式,得
PF1=a+ex0,PF2=ex0-a,
则a(a+ex0)=c(ex0-a),

由双曲线的几何性质知x0>a,则

整理得e2-2e-1<0,
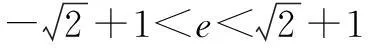

例6设椭圆上存在一点P,它与椭圆中心和与长轴一个端点的连线互相垂直,求椭圆离心率的取值范围.
解设椭圆方程为

A为右顶点(a,0)、P(x0,y0).
∵PO⊥PA,

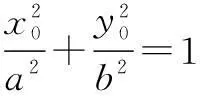
∴(a2-b2)x02-a3x0+a2b2=0,
(x0-a)[(a2-b2)x0-ab2]=0.




评注如果由题目条件,可将圆锥曲线上某一点的坐标用基本量a,b,c表示,就可以根据圆锥曲线的封闭性(半封闭性),建立不等式,从而得到离心率的取值范围.
五、利用二次方程根的判别式
解由曲线C与直线相交于两点,知方程组
有两组不等的根.消去y并整理,得
(1-a2)x2+2a2x-2a2=0,

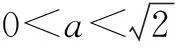
双曲线的离心率


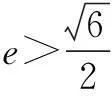
即双曲线离心率e的取值范围为
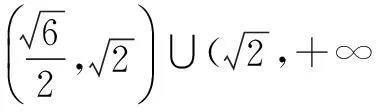
评注圆锥曲线与直线交点的个数可以转化为方程解的个数问题,用二次方程根的判别式可求出参数的范围,从而求出离心率的范围.
六、利用基本不等式

解由题意PF1+PF2=2a,F1F2=2c.
由∠F1PF2=90°,得
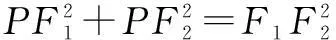

所以PF1·PF2=2a2-2c2.
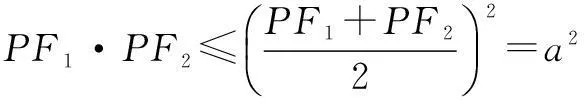
得2a2-2c2≤a2,
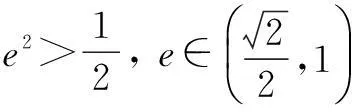
评注一定不能忽视基本不等式在求取值范围问题中的作用.
求圆锥曲线离心率的取值范围时需要因题制宜找出题中隐含的不等关系,构造含a、b、c的齐次不等式,进而转化为含e的不等式,最后求出离心率的取值范围.

