活用向量的数量积解非向量题
活用向量的数量积解非向量题
肖建平
(广东省兴宁市第一中学,514500)
向量作为一种解题工具,应用极为广泛,一直是高考和高中数学联赛的重点考查内容.向量知识融数形于一体,为我们解决数学问题提供了更为广阔的思维空间.本文通过构造向量、活用向量的数量积把一些非向量的代数题转化为向量问题,从而使运算简捷,易学易懂.
一、求代数式的最值
例1(2015年浙江高考题)若实数x,y满足x2+y2≤1,则|2x+y-2|+|6-x-3y|的最小值是______.
解易知|2x+y-2|+|6-x-3y|≥|(2x+y-2)-(6-x-3y|=|3x+4y-8|.构造平面向量α=(3,4),β=(x,y),则


α·β=3x+4y.
因为α·β≤|α||β|,当且仅当α与β同向时取等号,所以

得|3x+4y-8|=-(3x+4y)+8≥3.

评注本题难度大.有参考答案是依据绝对值内式子的符号分类,去掉绝对值后转化为线性规划问题来求解,对运算求解能力的要求较高,且不容易想到.笔者通过构造向量的方法,简化了运算,容易理解掌握.
例2(2015年福建高考题)已知a>0,b>0,c>0,函数f(x)=|x+a|+|x-b|+c的最小值为4.
(1)求a+b+c的值;
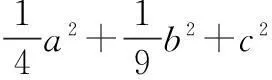
解(1)由f(x)=|x+a|+|x-b|+c≥|(x+a)-(x-b)|+c=a+b+c,当且仅当-a≤x≤b时等号成立,故a+b+c=4.
α·β=a+b+c=4.
因为α·β≤|α||β|,当且仅当α与β同向时取等号,所以
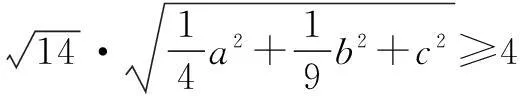

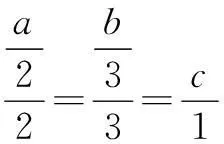

评注本题难度中等.可以利用柯西不等式求解.

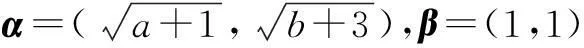
二、利用取等号求值
例4(2014年全国高中数学联赛陕西预赛题)若实数a,b,c满足a+2b+3c=6,a2+4b2+9c2=12,则abc的值是______.

评注本题难度较大.有参考答案分别利用作差,基本不等式,柯西不等式等三种方法进行解答.
三、证明不等式
例5(2014年福建高考题)已知定义在R上的函数f(x)=|x+1|+|x-2|的最小值为a.(1)求a的值;(2)若p,q,r是正实数,且满足且p+q+r=a,求证:p2+q2+r2≥3.
解(1)因为f(x)=|x+1|+|x-2|≥|x+1+2-x|=3且f(0)=3,所以f(x)的最小值为a,且a的值是3.
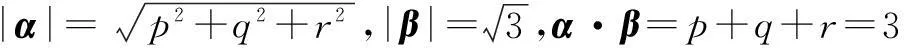
评注本题难度中等.可以利用柯西不等式求解.
四、思考
向量的教学如果仅止于课本,则无益于学生数学思维的培养,对数学问题的解决则没有深度和广度.如果能够引导学生进行适当的启发式教学,可培养学生举一反三的能力,提高学生学习数学的兴趣.本文通过学生熟知的向量数量积的计算公式进行多方面的应用,既开阔了视野,又为今后学习柯西不等式做了铺垫,可谓一举多得.
○短文集锦○

