一道高考函数题的解法探究
一道高考函数题的解法探究
邹蓓蓓
(江苏省如皋中学,226500)
本文以2015年江苏高考数学卷第19题为例,对高考函数的常考问题进行探究,以总结出解决这类问题的有效思路与解法.
一、试题呈现
题目已知函数f(x)=x3+ax2+b(a,b∈R).
(1)试讨论f(x)的单调性;

分析本题是导数、函数知识的综合应用题,主要考查含参函数的单调性、函数的零点判定定理,利用导数探究初等函数的单调性、极值和零点问题;考查学生综合运用数学思想方法分析与解决问题的能力以及逻辑推理能力,包括分类讨论思想、函数与方程思想、转化与化归思想以及数形结合思想.
二、思路与解答
1.第(1)问思路与解答过程
思路观察题目,要求函数f(x)的单调性,先求导,此时发现求导后f′(x)表达式中含有参数,这就要求根据参数的范围进行分类讨论.
解答f′(x)=3x2+2ax.

下面分三种情况讨论:
①当a=0时f′(x)>0,所以函数f(x)在(-∞,+∞)上单调递增;
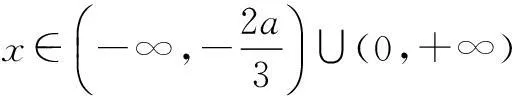

图7的四边形OABC及其内部,其中A(-3,3)、B(3,-1),C(2,-1),O为坐标原点.设z=2λ+μ,易知动直线z=2λ+μ过点B时z有最大值,且zmax=2×3-1=5.
评注本题以平面向量的线性运算为载体,考查了平面向量的线性运算、线性规划及其应用与等价转化的思想、灵活运用所学知识解决问题的能力.若不能正确地将其转化为λ,μ的线性规划问题则无从下手.

2.第(2)问思路与解答过程
分析本题第(2)问考查学生对函数零点的判定定理的理解与掌握,要求学生利用题目已知条件通过转化推理最终得出满足条件的结果.


又,因为b=c-a,所以

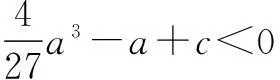



f(x)=x3+ax2+1-a
=(x+1)[x2+(a-1)x
+(1-a)].
因为函数有三个零点,故x2+(a-1)x+(1-a)=0有两个异于-1的不等实数根,


综上所述c=1.


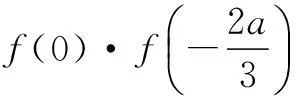


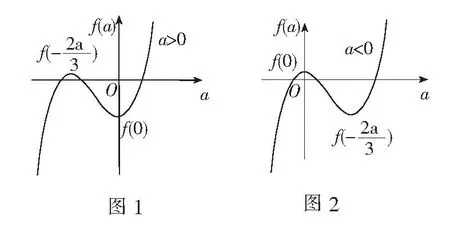
又∵g(a)是一个连续函数,
∴g(a)的图象如图3所示.



∴只有当c=1时,才可满足上述方程,
此时f(x)=x3+ax2++1-a
=(x+1)[x2+(a-1)x
+(1-a)].
∵函数有三个零点,
∴x2+(a-1)x+(1-a)=0有两个异于-1的不等实数根,


综上所述:c=1.
评注可以发现,函数与导数的结合,考查函数的单调性,函数零点问题是一种非常常见的题型.在这道江苏考题中,第(1)问涉及参数,要求分类讨论并不难.数学问题之间往往有一定的联系.第(2)问在得出函数单调性基础上,运用函数零点判定定理对题目条件进行转化,而数形结合思想的运用使题目条件由繁到简,由难到易,加速了问题的解决.
函数零点问题是高中数学新课标的新增内容.这类问题往往考查零点存在性、零点的个数等,要求考生能够结合函数图象,理解函数的零点与方程的根的联系,转化为判断方程根的存在性及根的个数.以下是函数零点的几种处理方法:
①解方程(方程思想)
方程f(x)=0的解就是函数y=f(x)的零点(也就是函数f(x)图象与x轴交点的横坐标),且方程f(x)=g(x)的解就是新函数y=f(x)-g(x)的零点(也就是函数y=f(x)与函数y=g(x)图象交点的横坐标).因此,可以通过研究方程或函数图象解决函数零点问题.
②构造函数法
函数h(x)=f(x)-g(x)的零点个数就是函数y=f(x)与函数y=g(x)图象交点的个数,可以通过作出函数y=f(x)与函数y=g(x)图象解决问题.
函数作为压轴题是历年来高考的热点,一般以函数为载体考查学生的基本数学素养以及运用数学思想分析、探究和解决问题的能力.近几年江苏高考数学的导数与函数问题,承继了以往“逻辑性、探索性、综合性”的特点,更注重于对“四基”的考查,即基础知识、基本技能、基本数学思想和基本数学活动经验.纵观江苏省近几年的高考函数题,其中最主要涉及的数学思想方法有化归与转化、数形结合、分类讨论等.数学思想方法的掌握程度和思维理解能力的高低决定着高考分数的高低,数学试题的考查形式千变万化,但是万变不离其宗,其中蕴含的知识点以及数学思想方法却是相通的,掌握了其中的数学思想方法便能抓住解题的关键.

