浅谈数学概念教学

中国人民大学附属中学　　100080　　吴中才

本文是海淀区重点关注课题《普通高中数学联合备课有效性研究》(课题编号：HDGH2015056)的阶段性研究成果



浅谈数学概念教学

中国人民大学附属中学100080吴中才

本文是海淀区重点关注课题《普通高中数学联合备课有效性研究》(课题编号：HDGH2015056)的阶段性研究成果

【摘要】数学离不开推理，推理又离不开判断，而判断又是以概念为基础的．因此，数学概念在数学推理与数学教学中有着至关重要的作用.针对概念获得的两种基本方式——概念形成与概念同化，概念教学通常包括四个主要环节：概念的引入、概念的形成、概念的明确(辨析)、概念的精致．

【关键词】概念;数学概念;概念教学

概念是反映事物本质属性的思维形式.正确的概念是科学抽象的结果.人们在实践的基础上得到了丰富的感性认识材料，经过去粗取精、去伪存真、由此及彼、由表及里的改造过程，舍掉了事物的一些次要方面，保留了事物的本质属性，形成了概念．

例如“积分”的概念，分割→求和→求极限，其中分割要求无限细.将区间等分并不是它的本质特征，只要让所有区间的长度均趋近于0即可.而教材给出的两个例子(一个求曲边三角形的面积，一个求变力做功)都是采用等分的办法，在这两个例子的基础上讲述积分的概念，就需要澄清区间的分割并不一定要等分，更要让学生明白为什么要等分(方便求和).另外，取小矩形的高时，两个引例取的都是小区间的端点处的函数值，这也不是本质特征，其实在小区间内任取一点处的函数值均可作为小矩形的高，教学时也要让学生明白为什么取端点函数值(还是方便计算)．

数学离不开推理，推理又离不开判断，而判断又是以概念为基础的.因此，概念不清，数学推理寸步难行.所以，有人说概念是思维的细胞．

例如，两个平面平行的概念是我们研究两平面平行的判定和性质的基础，如果不清楚两个平面平行的概念，就无法证明两个平面平行的判定(运用反证法的思维起点就是定义)，也无法研究两平面平行的性质定理了．

1概念的分类

数学概念分为两类：一类是对现实对象或关系直接抽象而成的概念；另一类是纯数学抽象物，这类概念是抽象逻辑思维的产物，是一种数学逻辑构造，没有客观实在与之对应，这类概念对建构数学理论非常重要，是数学深入发展的逻辑源泉．

例如，直线、平面、异面直线等就是直接抽象而成的概念；集合、函数、方程等则是纯数学抽象物．

2概念的掌握

概念的掌握又称概念的获得，一般有两种基本方式──概念形成与概念同化.这里，概念形成侧重指由具体到抽象、由特殊到一般、经过分析综合去掉非本质特征，保留本质属性的过程.概念同化则指依赖学习者认知结构中原有的概念，以定义的方式直接向学习者提示概念的本质属性的方式.前者更适合低年级学生，后者更适合高年级学生.在下面的“概念的形成”环节，包括概念形成与概念同化两种不同的获得方式．

认识论原理告诉我们，人们不可能一次地和孤立地认识一类事物的本质特征，而是用联系的观点，并且要经历一个由感性到理性的发展过程.因此，我们不能孤立地来谈论概念教学，应该把概念放到整个体系中去考察，但要分阶段处理．

例如，“函数”在初中是从运动变化的角度，用变量的观点进行定义的，主角是变量，而变量往往有着一定的实际意义；高中则是以集合论为基础，用对应(映射)的观点进行定义的，突破了变量的局限，如理解y=1是否是函数，理解数列是特殊的函数，用映射的观点就容易理解了；到大学还会讲到隐函数，将函数与方程联系起来了，同时还要注意到函数与方程的区别.同一个概念在不同阶段可以得到不同的发展，但在不同阶段也应当有不同的教学要求．

3概念的教学

概念教学一般有四个主要环节：概念的引入、概念的形成、概念的明确(辨析)、概念的精致．

概念的引入一般结合学生已有的知识经验和生活经验，让学生感受到学习概念的必要性，体会到概念的作用.常常采用从类比引入、从旧知引入、从需要引入等方式.例如，球的概念可以类比圆的概念引入，二面角的概念可类比平面角的概念引入．

在概念的形成环节，要引导学生思考、概括，促进学生对概念的有效同化，可以从以下几点设计教学：(1)向学生提供适当数量、适当强度的刺激模式，以便于学生分析、比较；(2)让学生进行充分的自主活动，使他们有机会经历概念产生的过程，并从共同属性中抽象出本质属性；(3)概括成概念后，教师适当引导学生对认知结构中的新旧概念进行分化，并将新概念纳入到已有的概念系统中去．

概念的明确需要从概念的内涵和外延两个方面来考虑.明确概念之后，还要把概念纳入到概念体系中，去明确概念间的关系．

概念的精致实质上是对数学概念的内涵与外延进行尽量详细的“深加工”，对概念要素与关键词进行具体界定，获得概念的某些限制条件，以使学生建立更清晰的概念表象，对概念的细节把握更加准确，等等.概念的精致通常表现为对各种可能的特例进行剖析，分析可能发生的概念理解错误，理解概念的各种变式，还包括掌握概念的多元表征(如形象表征、符号表征等)，并能在各种表征间灵活转化，这也是数学概念教学的基本策略．

下面看一个“函数极值”概念的教学设计案例：

环节一复习旧知

问题1：什么叫函数的零点？怎么表示函数的零点？(一般地，如果函数y=f(x)在实数a处的值等于零，即f(a)=0，则a叫做这个函数的零点.要注意零点是使得函数值为0的自变量取值，不是函数值，更不是指点(a，f(a)).)

问题2：如何利用导数判断函数的单调性？(如果在(a，b)内，f′(x)>0，则f(x)在此区间是增函数，(a，b)为f(x)的单调增区间；减函数类似.)

环节二概念引入

在群山之中，各个山峰的顶端，虽然不一定是群山的最高处，但它却是其附近的最高点.同样，各个谷底虽然不一定是群山之中的最低处，但它却是附近的最低点．

环节三概念形成

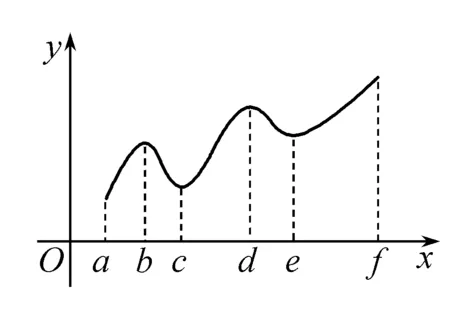
函数有增有减，其图象就象是绵延的群山.这些“峰”、“谷”对应的函数值在它附近就是最大值或最小值，我们称之为极值．

已知函数y=f(x)，设x0是定义域(a，b)内任一点，如果对x0附近的所有点x，都有f(x)

极大值与极小值统称为极值，极大值点与极小值点统称为极值点．

环节四概念明确

问题3：定义中“x0附近”怎么理解？(可以理解为x0的一个小邻域(x0-ε，x0+ε)，其中ε>0.由此可见，极值是一个局部概念，一个函数的极值点不唯一.)

问题4：结合函数零点的概念，你认为学习极值点应注意什么？(极值点是指x0，不是指f(x0)，更不是(x0，f(x0)).)

问题5：找出图中函数f(x)的极值点，并说明哪些为极大值点，哪些为极小值点？

环节五概念精致

问题6：极大值一定大于极小值吗？极小值一定小于极大值吗？(不一定，极小值未必比极大值小.)

问题7：区间端点能成为极值点吗？(不可能，因为端点另一侧情况不明确.)

问题9：对于可导函数f(x)而言，导数为0的点一定是极值点吗？(不一定，如y=x3在0处导数为0，但这不是极值点.)

问题10：f′(x0)=0和x0为极值点有什么关系？对可导函数f(x)而言，x0为极值点的充要条件是什么？(f′(x0)=0是x0为极值点的必要不充分条件，x0为极值点的充要条件是f′(x0)=0且点x0左右附近的导数值异号.)

问题11：如何求函数的极值点？如何求函数的极值？(先求出导数为0的点，再检验这些点左右附近导数值是否异号.如果左侧大于0，右侧小于0，则为极大值点；极小值点类似.求出极值点处的函数值就是对应的极值.)

问题12：已知函数f(x)=x3+3ax2+bx+a2在x=-1时有极值0，则常数a，b的值是多少？(注意检验!巩固x0成为极值点的条件.)

上面的教学设计兼顾了学生已有的生活经验和知识经验，突出了对事实性知识和过程性知识的理解，将缄默状态下的概念全方位激活，有效地在学生已有的知识结构上建构了新的知识体系，有助于学生对新概念的形成与同化．概念在数学推理中的作用重大，因此围绕着概念的内涵和外延进行的思辨设计在教学中也至关重要．当然，并不是所有概念的教学都要如此设计，尤其是对直接抽象而成的数学概念的教学，往往更要注重生活经验的举例，以及概念形成的抽象概括过程．