注重能力培养 优化二轮专题复习课教学——以“三角形中的最值与范围问题”为例



注重能力培养优化二轮专题复习课教学——以“三角形中的最值与范围问题”为例

江苏省如皋市教育局教研室226500万国全

高三二轮复习一般安排在3—4月份，历时两个月左右，是在一轮全面复习基础上的教学，承担着提升学生能力的任务.此阶段复习对教师的要求较高，是对教师能力水平的考验.如何进行二轮专题复习课教学是不少教师感到困惑的问题，本文结合“三角形中的最值与范围问题”的课堂教学实录及听课调研的情况，谈谈二轮专题复习课教学及其优化.

1课堂教学实录

师：三角形中边、角等的范围与最值问题是高考的常考问题，也是学生感到困难的问题，通过本节课对几道例题的研究，力争使同学们掌握解决这类问题的思路方法，形成解决这类问题思维导图.课前，大家都已解答了讲义上的三道例题，通过收阅你们的解答，发现了一些典型解法，下面请×××，×××同学，将各道例题的各种解法，板演到前后黑板指定的位置上.

学生展示了以下两种解法.

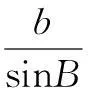
l=a+b+c

=2(sinA+sinB+sinC)

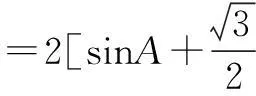
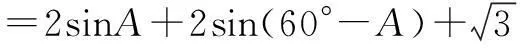
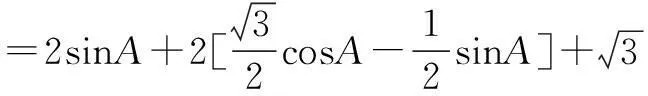
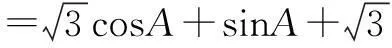
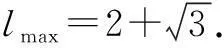
师：请给出解法的同学说说你的思路.

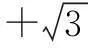
师：请给出法二的同学说说你的思路.

生2：方法二将问题转化为二元函数问题，对于二元函数，注意运用基本不等式求最值.

师：将问题变式成求周长的范围，用何法？

生3：用基本不等式法(即法二)不能解决，法一能解决.

师：求范围问题，若能转化成函数问题(法一中，令sin(60°+A)=t，即为一次函数)，运用函数性质往往可求出所求的范围.

例2在锐角△ABC中，角A、B、C所对的边分别为a、b、c，且c2=a2+b2-ab，设m=(sinA，1)，n=(6cosC，cos2A)，试求m·n的范围.

一学生给出了以下解法.

师：这种解法正确吗？若有不同意见，请上黑板来修正.

另一学生自动上黑板修正.

师：由此题的解答，提醒我们要注意什么？

生4：注意关注角的范围.

师：很好.求函数值的范围需注意函数的定义域，因为函数的最值或函数值范围随定义域的变化而变化.

例3△ABC的内角A、B、C，所对的边分别为a、b、c，若b、a、c成等差数列，a=6，求△ABC面积的最大值.

学生们给出了四种解法.

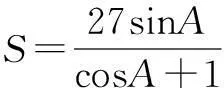
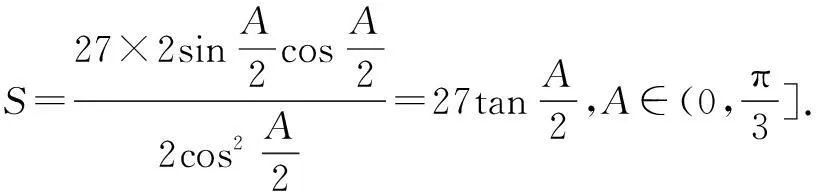
由正切函数的单调性知

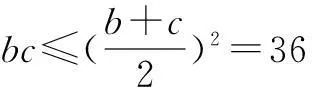
则问题转化为圆弧上点到点(-1，0)连线的斜率的有关问题.

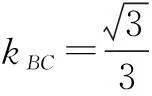
由图可知，

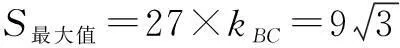
师：请给出解法的学生，说说你的思路.

生7：法三是通过变换将问题转化成含有两个变量

师：通过三道例题的学习，你能得到解决三角形中的有关最值与范围问题的解题思路了吗？

在学生独立思考一段时间后，教师让学生小组合作交流，并请各组代表展示小组研究成果.最后师生共同得出：

三角形中最值与范围问题的解题思路：①运用正弦定理或余弦定理，将问题转成三角函数问题或一元函数问题或二元函数问题等；②对于三角函数问题可转化成同一个角的同一个三角函数问题解决；对于一元函数问题，注意运用一次函数、二次函数的知识或求导法解决；对于二元函数问题，注意运用基本不等式或式子的几何意义解决.

师：你能构建解决此类问题的思维导图吗？

在学生展示的基础上，师生共同完善，并板书思维导图：

师：在求解过程中易出现什么错误？即要注意什么？

生：注意自变量的取值范围，即角或边的范围.

教师板书：注意自变量的取值范围.

师：请同学们订正整理本节教学内容，并完成以下练习：

练习：1.在钝角△ABC中，角A、B、C所对的边分别为a、b、c，a=1，b=2，则最大边c的取值范围是____.

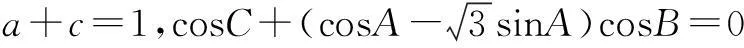
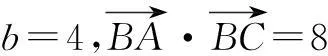
(1)求a2+c2的值.

4.△ABC的外接圆半径为1，角A、B、C所对的边分别为a、b、c，实数x满足，abx=a+b，试求x的取值范围.

2关于优化二轮专题复习课的几点思考

2.1　选准问题专题

二轮复习是在一轮全面复习基础上的教学，因而其教学目标任务是突出重点知识，弥补知识缺陷，提升学生解题能力.突出重点知识、弥补知识缺陷可运用专项练习的方法予以实现，提升学生解题能力则应通过专题复习的方法予以实现.在教学实践中，很多专题复习课上成一轮复习课的浓缩，课堂教学内容显得散而多，学生没有新的收获，能力没有得到提升.其主要原因是，课题确定不科学，仍以三角与向量、函数与导数、数列、不等式、解几等学科知识内容为课题进行复习.二轮专题复习课课题的确定应以问题为导向，问题应为高考的常见问题或学生的弱点问题，因此，要认真研究历年高考试题和学生一轮复习的状况，从中找出问题，并将其确定为复习专题.这样的专题往往是小专题，用一课时或二课时可以解决.“三角形中的最值与范围问题”是三角高考内容中的常见问题和学生感到困难、容易发生错误的问题，本课例中将其确定为复习课题较为科学.

2.2　选好教学内容.

课题确定后，如何确定教学内容？如何编拟复习讲义？

2.2.1要准确确定教学目标

教学内容确定的依据是课堂教学目标.在二轮专题复习课的课堂教学中，大量存在着知识整理现象，重复了一轮复习内容，浪费了宝贵的课堂教学时间，其原因是一些教师误认为基础知识的掌握也是二轮专题复习的教学目标，未能明确提高学生解题能力才是二轮专题复习课的主要任务.如何使提高学生解题能力落到实处？应把二轮专题复习课的教学目标确定为：通过例题教学，使学生掌握解决某类问题的思路方法和形成思维导图，克服学生的有关薄弱点.这样，学生在今后面对有关问题时，思维就有了方向，问题的解决就有了希望.

2.2.2要精心选择典型例题

要注意专题性.在二轮专题复习的课堂教学中，存在着选择的例题所反映的核心问题散而杂的现象，不利于形成解决一类问题的解题思路和思维导图.如在一节有关三角问题的专题复习课上，一位教师选了三道例题，例1是已知三角函数值，求值和求角问题，例2是运用三角函数定义求点的坐标问题，例3是通过三角函数图象求解析式的问题，三个例题所涉及的问题各异，不利于学生形成解决一类问题的思维主线，难以在学生头脑中留下深刻的印象.例题的选取要紧扣教学专题，涉及的问题不可多而杂，要为形成解决一类问题的解题思路和思维导图服务.本课例中的例题均为三角形中的有关最值与范围问题.

要注意关联性.例题的选取要注意它们之间既要有区别又要有联系，通过对每道例题的不同解法的梳理，能形成解决一类问题的较为完整的解题思路.在本课例中，例1的解决，解法一是将问题转化成同一个角的同一个三角函数问题，运用三角函数的有界性解答，解法二是运用基本不等式解答；例3的解决，解法一是运用导数法，解法四是运用式子的几何意义，通过对各题解法的梳理形成了课例中所呈现的解题思路和思维导图.

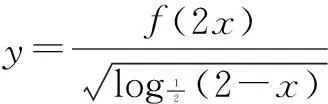
要注意迷惑性.即要注意所研究的一类问题中，学生易犯哪些错误，选择相关具有迷惑性的例题，让学生通过摔跤，强化印象，克服薄弱.在三角形最值与范围问题中，学生容易忽视角的范围和边的范围的限制条件，所以，在本课例中，通过选取例2来强化学生注意，克服学生弱点.

当前，市场上一些二轮专题复习资料上的内容，存在着繁多的现象，体现在：一是复习专题多，不少专题是知识性的专题，是一轮复习的重复；二是文字叙述多，不少文字是编者的思想，而不是学生的体会，学生难以入眼入脑；三是例题比较“散”，不能使学生形成解决一类问题的思维导图.所以二轮专题复习的内容，要以我为主，根据高考实际和本校本班学生实际，利用集体的力量，自选复习内容，不能照搬外来资料.

2.2.3优化课堂教学

坚持先练后讲.为了提升学生的能力，二轮专题复习所选例题，具在一定的难度，而在学生没有思考的情况下讲解，学生的思维往往跟不上教师的思维，影响学生学习的情绪；在学生练习后进行讲解，课前教师可摸清学生的学习状况，有利于实现课堂教学的针对性，避免教学的面面俱到.所以要坚持让学生先练、教师后讲的教学原则，以激发学生学习的兴趣，提高教学的有效性.

注重一题多解.一轮复习是分块(如三角、函数、数列、解几等)进行的复习，二轮复习必需打通各块知识，加强各块内容的联系，培养学生综合运用各块知识解决问题的能力.注重一题多解，可让学生多角度审视问题，综合运用各块知识解决问题，拓宽学生思维.多种解法既要来自教师，也要来自学生.学生经过一轮复习已掌握了一定的解题方法，班级上几十个学生就有几十个思维，学生们必会产生多种不同的解题方法.而来自学生的方法，符合学生们的认知特点，学生们易于接受；同时也能引起学生间的解题竞争，调动学生的学习积极性.在本课例中，学生给出了各种不同的解法，内容涉及到三角、二次函数、不等式、导数、解几等知识，加强了知识的横向联系，促进了学生对知识的融合，提高了学生的解题能力.

构建思维导图.构建一类问题解答的思维导图是专题复习的目标，因此，当学生给出每道题目的解答过程时，还要要求学生说出其解题思路和解题方法，以便学生掌握解题要点；当教师讲解难题时，不应讲解解题过程，而应讲解解题思路和解题方法.在课堂小结时，要善于将每道例题的解题思路和解题方法进行比较、联系，梳理出相关问题解答的整体思路，构建思维导图.在本课例的课堂教学中，教师让学生展示每题的解答过程后，还要求学生说出解题思路，在每题的解题思路方法提炼的基础上，进行课堂小结，形成了解决“三角形中的最值与范围问题”的思维导图.

注重整理巩固.二轮专题复习课的内容往往有一定的深度，需要及时订正整理，才能克服模糊认识、理清思路方法.在课堂上可安排5分钟左右的时间让学生自主整理，以促进订正整理的落实.要根据教学目标和学生仍存在的问题，选择巩固练习题，促进学生真正掌握所学一类问题的解题思路和克服薄弱环节.

突出学生主体.学生的能力不是教师“灌输”出来的，而是学生在活动中锻炼出来的.在课堂教学中，要让学生主动去想、主动去做、主动去说，才能突出学生的主体性，促进学生能力的提升.在实施先练后讲的课堂教学中，要让学生充分展示.课前学生已经对例题进行了解答，课上教师如果重新逐题讲解，学生必会索然无味，而让学生展示其研究成果，可让他们获得成功的喜悦，调动其学习的积极性.要注意选择典型的不同解法和典型的错误解答让学生展示，并注意让多名学生上黑板同时进行展示，以提高展示的效率.要让学生对展示进行评价，通过对不同方法的比较和选择，错误解法的识别和订正，以优化学生思维，提高学生能力.在这样的课堂上，教师的作用是点拨提炼，即点拨学生思维的方向，提炼解题规律和注意点(在学生提炼不到位时).要注重合作学习.对于解题思路的总结、思维导图的构建和难题的解答等重点难点内容，可采用合作学习的方法，发挥学生群体的力量加以解决.群体的智慧是无限的，学生们通过合作交流，思维碰撞，相互启发，往往能找到问题的解法，而通过学生自己的主动思考得出的内容比起教师的灌输来印象要深刻得多.二轮复习期间，学生学习负担重，学习压力大，让学生展示其学习成果、采用合作学习的教学方式，可改变课堂教学生态，活跃课堂气氛，让学生处于愉悦的学习氛围中.