TED演讲：如何学习微积分(续)



TED演讲：如何学习微积分(续)

中国科学院林群

第三讲面积：级数的文字转换

如何测量面积？有没有一个计算公式？

我们所熟悉的，测量面积的自然方法，就是使用下和或上和

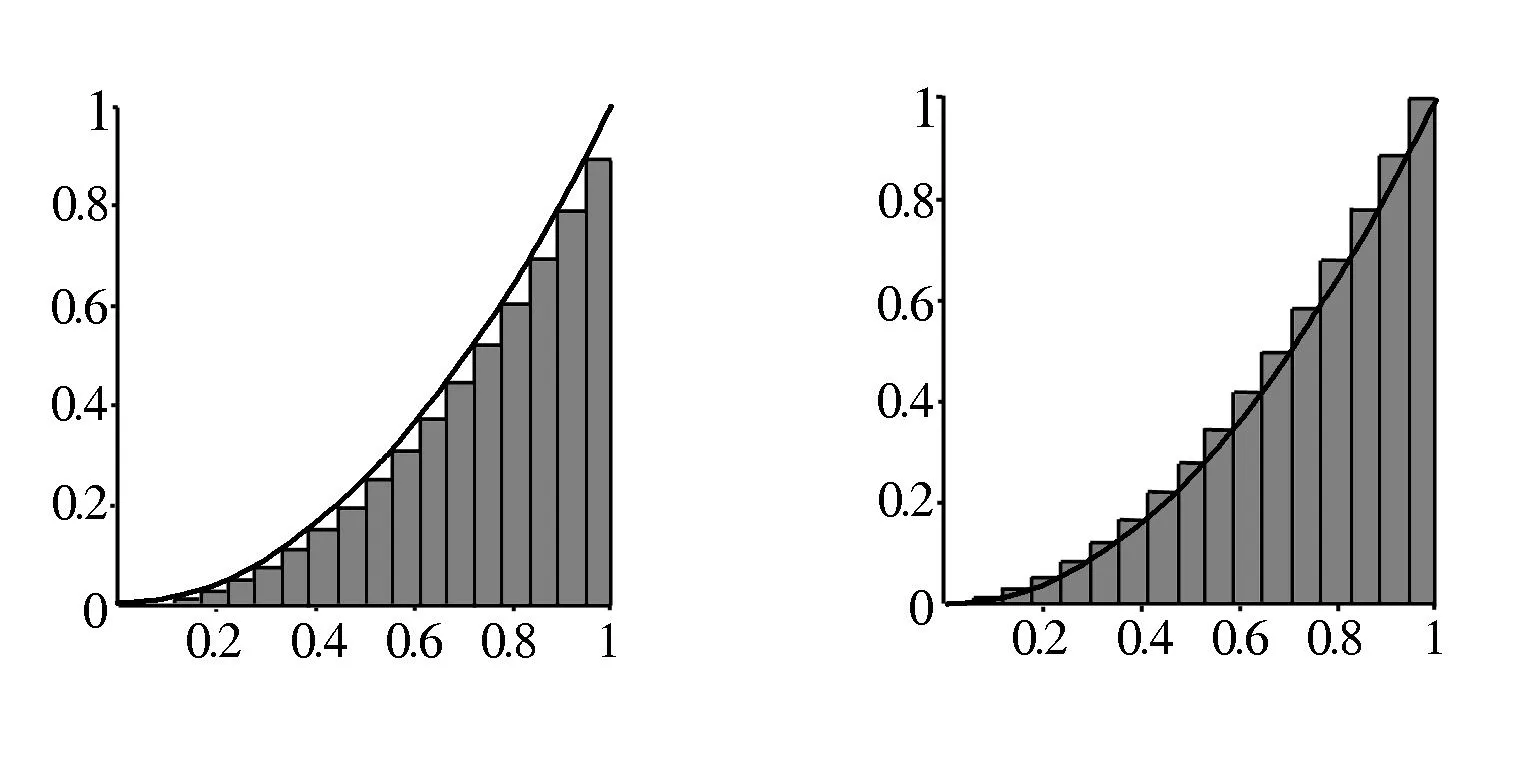
也使用比例表示

思想活动暴露如下：先想到，随着分点在增加，或细分下去，小矩形面积应该跟小曲边梯形面积相接近

同理，当分子与分母各自相加，应该也有

的过程或构造，达到彻底明白.

习题或案例求单位圆面积(内接多边形做下和，所有切线三角形做上和).

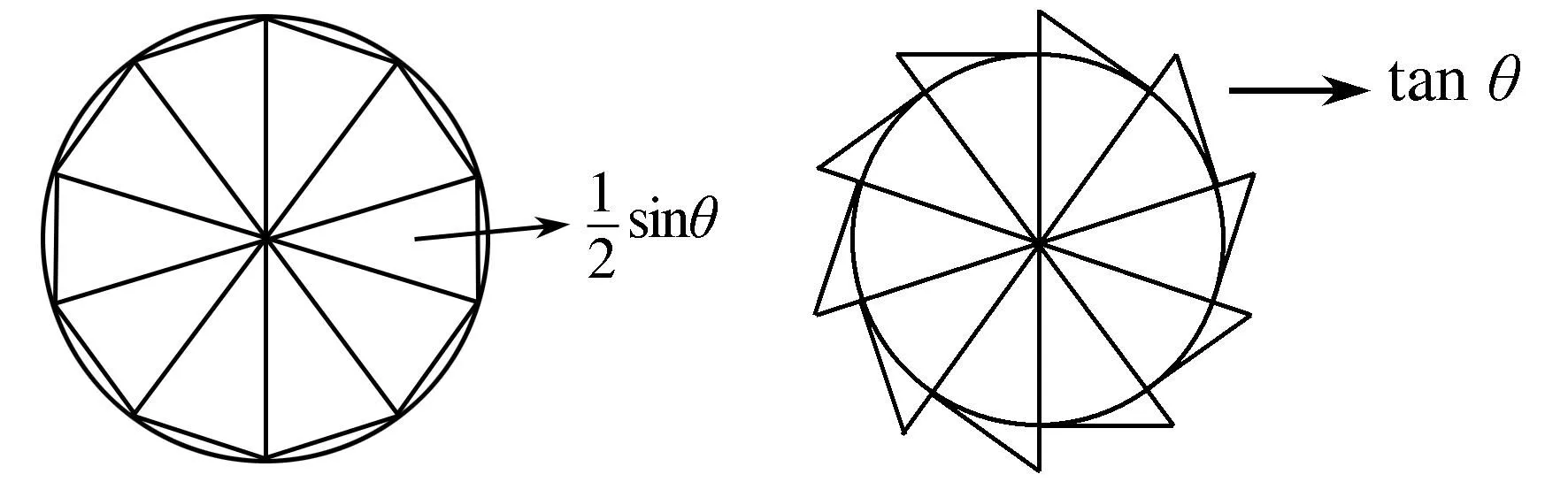
(不足近似)____　　(过剩近似)

上下和是测量面积的合理方法，但用它做计算，就很复杂.只能作为面积的一种定义.这是阿基米德公式.牛顿-莱布尼茨公式，则通过转换……(过程先不作解释)，将一团面积表示为一条高

=另一曲线的无限多个微分相加=一条高

第四讲由牛顿-莱布尼茨公式进入泰勒公式

以上几讲，表面上相等相似或一致：坡长、坡高以及面积的无限等式，本质上将同类项合并为级数的无限等式.但是数据复杂度在升高，量变发生质变：坡长与面积本是定义，计算复杂，坡高却是求函数值，计算简单许多.

但要求出函数值，可能还要用泰勒公式(但不必另起炉灶，只作为牛顿-莱布尼茨公式的陆续作用，见附录三).特别用于求圆周长与面积时，可得三连环公式

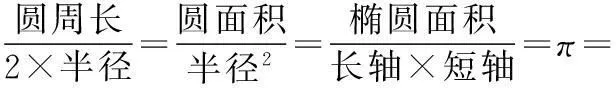
从图1中可以看出，当称样量在0.25～1.50g之间变化时，EDTA标准溶液滴定体积与称样量线性相关，说明氟化钙的溶解度基本保持不变。通过计算可得图1中钙(以碳酸钙计)质量变化的最大值约为9.4mg，即两次称样量之间碳酸钙的质量差在9.4mg之内都能满足实验方法分析要求。

所以，分子=分母.见附录三.这也见证了前面说过的：若没有级数，微积分可能半途而废.

圆乃公众普遍关心的对象.得到三连环公式，即可收兵.有所为有所不为，知足者常乐.

到此可以说，

微积分=(牛顿-莱布尼茨公式)+泰勒公式

(若没有泰勒公式，牛顿-莱布尼茨公式可能半途而废).这两大公式乃微积分的正副统帅.反之，课本上公式太多，千军万马，多属无病呻吟.

附录三说书版↔符号版

前几讲，暴露微积分的思想活动.先想到(有了瓮)再施行(再捉鳖)，有的放矢，事半功倍.有了思想，译成符号，一唱一和.

符号表示：当山坡表示为f(x)，则斜率与微分分别表示为

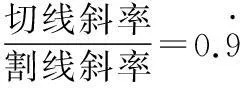
其中f′(x)=?怎么捉住或猜出？使最后右边的比例趋于1即是.例如捉住或猜出(习题)

加上积分符号，牛顿-莱布尼茨公式写成

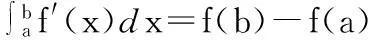
亦即第0讲总结所指的无限算术.

无限多个数据相加=两个已知数据相减.

泰勒公式

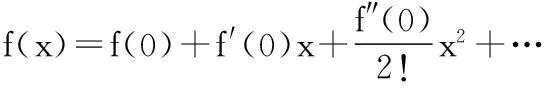
的推导，不必另起炉灶，由牛顿-莱布尼茨公式陆续改写(一道习题)，或使用比例表示

=0.999….

为什么第四讲会有三连环公式？请看下面转换，如何将被积函数改写为微分形式，从而可用牛顿-莱布尼茨公式，变为可计算.

习题

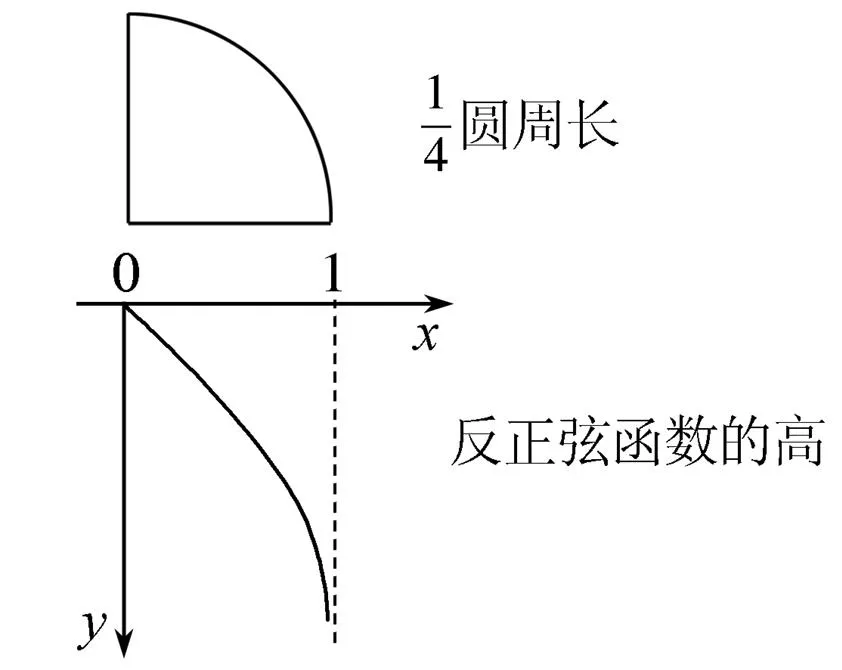
1.单位圆周长

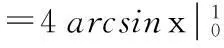
2.半径r的圆周长

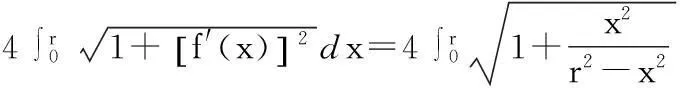
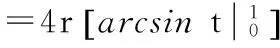
=4rarcsin1=8rarctan1.

3.单位圆面积

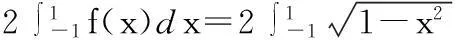
=2arcsin1=4arctan1.

4.半径r的圆面积

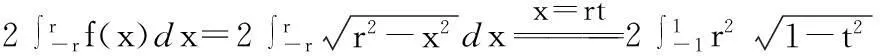
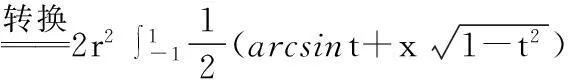
5.椭圆面积

以上关键在于被积函数改写为微分,虽然等价但不等效,由计算复杂变到简单.

以上历史难题，终于统一到反正弦的高.

剩下这个高如何求？要靠泰勒公式,得到下面的计算公式.

6.2arcsin1=4arctan1=π

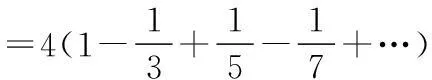
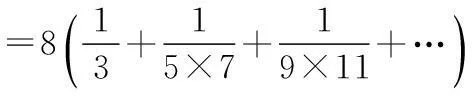
这里自动写出后面的项.

7.如何将被积函数改写为微分呢？上面看到，即使对圆也不容易，对大多数初等函数根本不可能.所以，牛顿-莱布尼茨公式只能断其一指.那么，有没有更好的公式，至少能断初等函数的十指呢？这就是第二版将讨论的欧拉积分公式.

(续完)