一花一叶一世界一思一悟一禅通
——对一道解析几何题的探究与启示
☉江苏省南京市东山外国语学校高中部 郭俊
一花一叶一世界一思一悟一禅通
——对一道解析几何题的探究与启示
☉江苏省南京市东山外国语学校高中部 郭俊
一道好的例题往往意境深远、蕴含着很多探究的素材,具有较大的再生能力与发展的空间.因此,我们在选题评讲时不能只看表面,要多角度地考虑问题,使思维呈现辐射状展开,开阔视野,拓展思维,多方位引导学生对试题进行剖析、探究,立足于问题的本质,最终提高学生的思维能力.下面本文从一道例题出发,层层深入探究,以求进行全方位的审视与研究,旨在通过这道题的剖析收获一片,达到“一花一叶一世界,一思一悟一禅通”的境界,使数学课堂教学不断走向高效,现整理如下,供读者参考!
(Ⅰ)求直线A1P与A2Q交点的轨迹E的方程;
(Ⅱ)若过点H(0,h)(h>1)的两条直线l1和l2与轨迹E都只有一个交点,且l1⊥l2,求h的值.
一、重视细节闯难关
分析:对于这道题目绝大多数学生在解答(1)时分析条件不仔细,运算中推理不严谨,没能发现曲线的限制条件,找出方程中变量的取值范围,造成所求的轨迹不具备完整性,也就不能排出椭圆的四个顶点,也就引起第(2)问解答错误.对优秀学生的访谈可知也是由于没有正确地求得曲线的范围,引起了第(2)问的失误.由此可见,在教学中只注重求轨迹方程的解题技巧,而不重视对本质的揭示是一个普遍存在的严重问题,必须引起我们的警示和反思.下面通过详细的解题过程来分析:
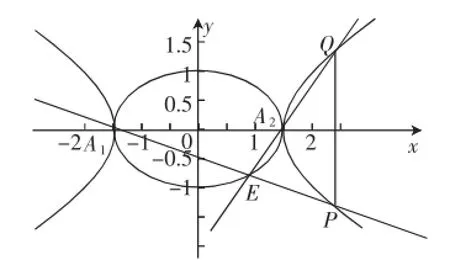
图1
直线A1P的方程是
直线A2Q的方程是
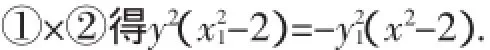
将l1:y=kx+h代入+y2=1,整理得(1+2k2)x2+4khx+ 2h2-2=0.
若l1与椭圆相切,则Δ=16k2h2-4(1+2k2)(2h2-2)=0,即1+2k2=h2;
同理,若l2与椭圆相切,则
由l1、l2与轨迹E都只有一个交点包含以下四种情况:
(1)l1、l2都与椭圆相切,即1+2k2=h2,且1+2·=h2,消去h2得=k2,即k2=1,从而h2=1+2k2=3,即h=;
(2)l1过点A(1-,0),而l2与椭圆相切,则k·(-)+h=0,1+2·=h2,得
(3)l2过点,而l与椭圆相切,则-·
1+h=0,1+2k2=h2,得
(4)l1过点A(1-,0),而l2过点A(2,0),则k·
通过上面的解题过程分析,现在我们来分析解答中的一些细节问题:(1)交轨问题是否一定要解方程求交点?通过联立①②的方程组,可以得到如何消去参数x1、y1?这有一定难度,部分考生会卡在此步.如果变形得到,再化简便得到轨迹E的方程,总的来说,其实还是考查常规的相关点法(即代入法).(2)解方程用到的是加减消元法,但如果我们采用乘法,由①×②可以不解方程,更快地得到结果.这种“设而不求”,体现了更高的数学思想与方法技巧,可见我们在引导学生分析时不能只注重解法,要探究其本质.解题分析时最好还补充这个例子:椭圆的长轴为是AA,12P是椭圆上的任一点,求A1P与A2P的垂线的交点Q的轨迹.如法炮制,不解方程容易得到轨迹方程为,还是一个椭圆(如图2).
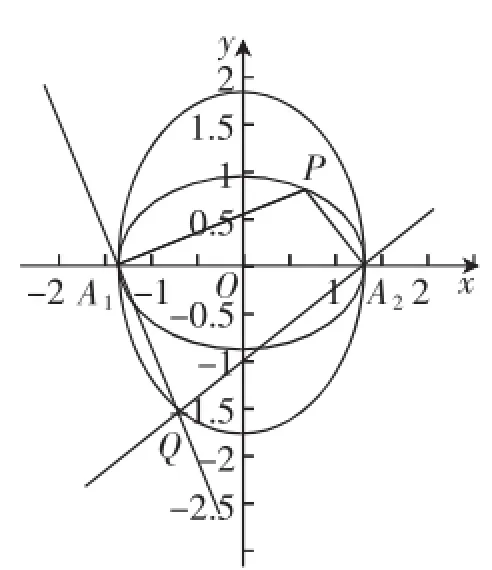
图2
二、翩翩起舞相伴随
通过对上面的“优美解”,我们在分析过程中还应挖掘到:“点P(x1、y1),Q(x1、-y1)关于x轴对称”,“点H(0,h)在y轴上,根据对称性可知l1和l2与y轴的夹角都是45°”,虽然“优美”欺骗了学生,但是作为老师的我们“充分利用对称性”造成了不完美,但若把这两个害群之马“收编”回一个完整的椭圆中,却又可以有更多发现,这也算是一种“补美”吧.从中可以发现挖掘:双曲线-y2=1与椭圆+y2=1相映成趣,如图3,这样就考虑一个类似的问题:已知椭圆+y2=1的左右顶点分别是A1、A2,PQ为与A1A2垂直的弦.求直线A1P与A2Q交点的轨迹E的方程.通过前面的方法可求得直线A1P与A2Q交点的轨迹E的方程是双曲线-y2= 1,这样就完全类似上述方法可得一般性的结论:(1)如图4,双曲线=1的顶点分别是A1、A2,弦PQ⊥A1A2,则直线A1P与 A2Q 交点的轨迹是椭圆=1(.2)如图5,椭圆=1的左右顶点分别是A1、A2,弦PQ⊥A1A2,则直线A1P与 A2Q 交点的轨迹是双曲线=1;当a=b时,双曲线为等轴双曲线,椭圆变为圆,结论仍成立.因此点P(x1,y1)、Q(x1,-y1)关于x轴对称,因此点P是主动点,交点E是被动点.如果引入伴随曲线的概念,可知椭圆的伴随曲线是双曲线,双曲线的伴随曲线是椭圆.
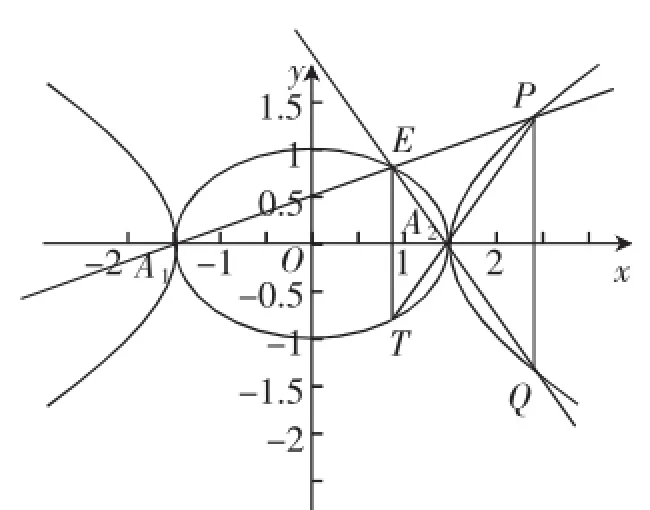
图3
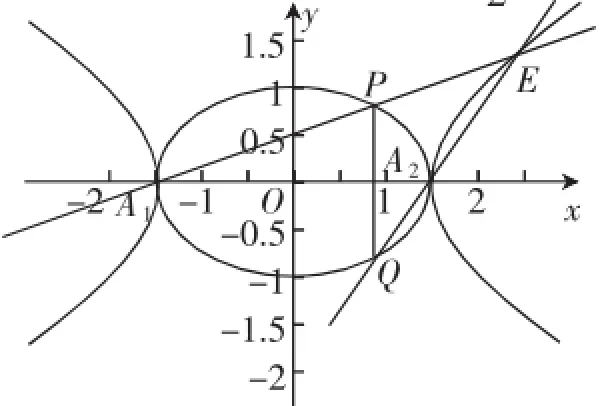
图4
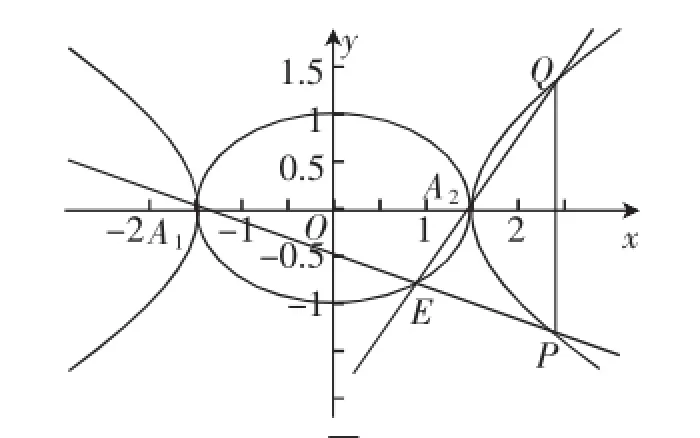
图5
这时想起庞龙的《两只蝴蝶》:“我和你缠缠绵绵翩翩飞,飞越这红尘永相随……”
双曲线与椭圆就像翩翩起舞、形影不离的蝴蝶;更像肝胆相照、情同两手的朋友.因此我们结合题目条件再深入探究发现:椭圆的长轴顶点分别是A1、A2,P是双曲线上的动点,直线A1P与A2P分别与椭圆C1交于点E、T,则直线ET⊥x轴;E是椭圆C1上的动点,A1E与A2E分别与双曲线C2交于点P、Q,则直线PQ⊥x轴.从中可发现:这是美妙和谐的对偶,你中有我、我中有你,多么像息息相关、比翼双飞的情侣!
三、以美导真启新篇
数学家波利亚曾形象地指出:“好问题同某种蘑菇有些相像,它们在成堆地生长,找到一个以后,你就应当在周围找一找,很可能附近就有好几个.”因此问题解决后应当让学生从解决的问题出发,运用类比、联想、特殊化和一般化的思维方法,派生出一些常规问题和开放性的问题,使问题“成片开发”.我们再从上面的解答过程来分析,只需再深入就可以注意到:结果中出现了1,,这个特殊的数列,这仅是巧合吗?通过探究可发现:(1,0)是椭圆的焦点,(,0)是椭圆的顶点,(,0)是双曲线的焦点,其中是否隐藏了更深的奥秘?又怎能不令人浮想联翩,产生窥探到底的欲望!通过探究并用几何画板演示可得.
探究1:过点H(0,h)的两条直线l1和l2与椭圆mx2+ ny2=1都只有一个交点,且l1⊥l2,求h的值.
解析:点H(0,h)在y轴上,根据对称性可知l1和l2与y轴的夹角都是45°,不妨设l1的方程是y=x+h,代入椭圆方程mx2+ny2=1,得mx2+n(x+h)2=1,即(m+n)x2+2nhx+nh2-1=0.
因为l1与椭圆相切,所以Δ=4n2h2-4(m+n)(nh2-1)= 0,化简得,于是在椭圆=中,h2a2+b2,四个点连成的正方形刚好与椭圆外切,四个点在以点O为圆心为半径的圆上.这就再次展现了一种对称美,通过这个特殊化的细节与部分无意间昭示了整体的更多隐秘.我们可探究到:椭圆的两条切线刚好是正方形所在直线,这是特殊的,能不能去掉这种特殊要求?
首先回到最对称的曲线——圆中,易知圆x2+y2=r2的相互垂直的两条切线的交点E的轨迹还是圆,方程是x2+ y2=2r2.对于椭圆呢?
探究2:求证:椭圆C1的相互垂直的两条切线的交点T的轨迹是以点O为圆心为半径的圆.
证明:如图6,设交点T(x0,y0),当过点E的切线l1不垂直于x轴时,其方程为y-y0=k(x-x0),k为斜率,代入椭圆方程,得(a2k2+b2)x2+2a2k(y0-kx0)x+a2[(y0-kx0)2-b2]=0.
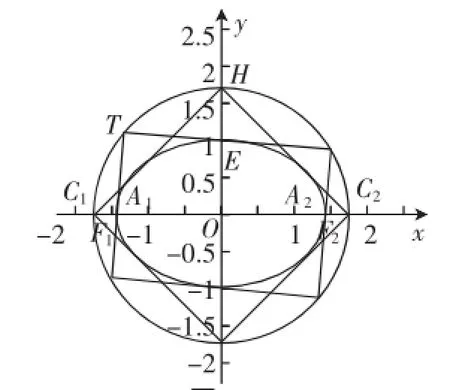
图6
因为l1与椭圆相切,所以Δ=a4k2(y0-kx0)2-(a2k2+b2)a2·[(y0-kx0)2-b2]=0,化成关于k的二次方程(a2-)k2+ 2x0y0k+b2-=0.
因为点T在椭圆外,且过点T的切线不垂直于x轴,
所以方程恒有两个根,就是两条切线的斜率k1、k2.
因为两条切线相互垂直,所以k1k2=-1,所以b2-= -(a2-x2
0).
以x、y代替x0,y0,得到x2+y2=a2+b2.
当过点T的一条切线垂直于x轴时,和它垂直的另一条切线必垂直于y轴,它们的交点为(a,b),(-a,b),(a,-b),(-a,-b),仍满足x2+y2=a2+b2.
反之,若点T(x1,y1)是圆x2+y2=a2+b2上任意一点,过点T可作椭圆C1的两条切线l1和l2.
当l1、l2中有一条无斜率时,易证l1⊥l2;
当l1、l2都有斜率时,由Δ=0整理得(a2-)k2+2x1y1k+ b2-=0,该方程的两个根就是两条切线的斜率k1、k2,而+=a2+b2,故k1k2=-1,所以l1⊥l2.
现在来看一个有趣的问题:已知长轴长为2a,短轴长为2b的椭圆在直角坐标平面的第一象限内移动,使它始终与两坐标轴相切.试求椭圆中心P的轨迹.
此问题若静止地从固定坐标轴的角度分析是有困难的.但将两坐标轴看成椭圆的动切线移动,问题就变为“求椭圆的两条互相垂直的切线的交点的轨迹”问题.利用探究2的结果:不论切线如何移动,其交点与原点的距离始终等于■a2+b2,由此可见原问题的椭圆中心P的轨迹为圆弧.通过进一步探究继续可得:
探究3:设椭圆+=1的两条切线的夹角为定值α,当α≠90°时,求两条切线的交点T的轨迹.(所求轨迹方程是(x2+y2-a2-b2)2tan2α=4b2x2+4a2y2-4a2b2)
探究5:抛物线y2=4ax的两条切线PA、PB的夹角为定值α时,求交点P的轨迹.
四、鉴古知今备高考
俗话说:经验丰富的人读书用两只眼睛,一只眼睛看到纸面上的话,另一只眼睛看到纸的背面.作为高考前线的数学教师,同样也要一只眼睛看到好题,另一只眼睛看到背面,才能真正做到鉴古知今,继往开来.如下+=1题:给定椭圆C:(a>b>0),称圆心在原点O,半径为r=的圆是椭圆C的“准圆”.若椭圆C的一个焦点为F(,0),其短轴上的一个端点到F的距离为(.Ⅰ)求椭圆C的方程和其“准圆”方程;(Ⅱ)P是椭圆C的“准圆”上的一个动点,过点P作直线l1、l2,使得l1、l2与椭圆C都只有一个交点,且l1、l2分别交其“准圆”于点M、N.(1)当P为“准圆”与y轴正半轴的交点时,求l1、l2的方程;(2)求证:|MN|为定值.
其实上,探究2与探究4得到的结果是前辈数学家早已得到的,它们的轨迹分别称为椭圆、双曲线的准圆,也称蒙日圆(蒙日,Monge,法国著名数学家,他提出一个难题:画一个圆,使其与三个已知圆正交.这是历史上最有名的100个初等数学难题之一).
从中也可以看出高考(或模拟)试题总有意无意地从经典的解析几何问题中寻找命题灵感,
五、对今后教学的启示
历年来解析几何问题一直是高考“重头戏”,一般情况下它的解答方法灵活多变且运算能力要求高,特别是在利用代数方法求解的过程中,往往会出现“过程冗长、运算烦琐”,而令我们“望而生畏、不战而退”.因此,我们在平时解决解析几何问题时就要引导学生学会“找路”、学会探究.正所谓“水本无华,相荡而成涟漪,石本无火,相击而发灵火.”因此在进行解析几何解题教学的过程中不要让自己的精彩讲解扼杀了属于学生的一切.要以探究为径,不断启发点燃学生的思维火发,暴露学生的思维过程,展示学生的思维成果,放手大胆地让学生去进行探究,把原本属于学生的时间还给学生,让他们来探究、来领悟.[1]比如本文从一道例题出发,通过猜想、验证和代数证明,将结论进行层层推进,形成了一个统一结论,这样对学生思维的培养是高效的,因此教师在平时的教学中要注意以下几点:(1)教师要善于捕捉探究资源,教师在教学中要用“研究者的眼光”去思考问题,将教学内容进行“再创造”,要有敏锐的观察力,使探究性教学成为常态教学;(2)教师要学会综合归纳.对于相互联系的问题,教师不仅要学会从不同侧面分析,更要在不同侧面分析的基础上,学会综合,从整体上得到共性,否则,遇题做题,不经过创造,难以达到一般的认识,对该类问题的认识只能是停留在表面程度上;(3)做数学研究不要轻易放弃自己的每个小小发现,通过类似研究的方式进行深度探究,或许它会给辛勤的数学研究者一个意想不到的惊喜.
总之,解析几何的教学如山如水,“一山一水一世界,一思一悟一禅通”.在这个过程中如果始终能以学生的思考、领悟为主线,不断以禅意践行“解题教学”之旅,引导学生守住“衣带渐宽终不悔,为伊消得人憔悴”的耐性,不断引领学生在解题中向悟法、得法、触类旁通、完善认知等方面靠拢,才可以让学生抵达“蓦然回首,那人却在灯火阑珊处”的最高境界.这样的教学让学生获得的不仅仅是知识,更重要的是拥有智慧!
1.林生.从一到高考题的开发与利用管窥解题教学[J].中国数学教育,2013(12).F


