小意外剪出大定义
☉浙江省温岭市新河中学 江庆君 李巧敏
小意外剪出大定义
☉浙江省温岭市新河中学 江庆君 李巧敏
《普通高中数学课程标准》(实验)指出:提供积极主动,勇于探索的学习方式,学生的数学学习活动不应只限于接受、记忆、模仿和练习,高中数学课程还应倡导自主探索、动手实践、合作交流、阅读自学等学习方式.这些方式有助于发挥学习的主动性,使学生的学习过程成为在教师引导下的“再创造”过程.在新课程的倡导下,探索、创新逐渐成为教师课堂教学的重点,有意栽花花不开,无心插柳柳成荫,在实际的课堂教学中往往有很多的“无心柳”,善于把握这些课堂中的意外,就会有意想不到的结果.
《二面角的平面角》第一课时,主要探索二面角平面角的定义,而本人在实际授课的探索过程中,却出现了一点小意外,于是将错就错得出大定义.
一、二面角平面角的定义
1.自己动手,发现疑问
师:在学习了异面直线所成角、直线和平面所成角之后,那么两个平面相交也应该有所成角.我拿出事先准备好的长方形硬纸板,沿中间线折成如图1所示.
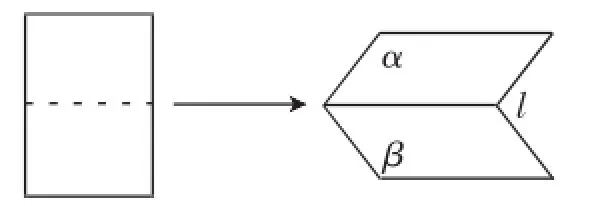
图1
结合实物给出二面角的定义:从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,记作α-l-β.
师:请问各位同学,二面角可以度量吗?用什么进行度量呢?就像前面曾经学过的线线角和线面角.
生:既然称为角,肯定可以度量,我想应该转化成平面角来度量.
对于一个确定的二面角,如何找到能度量此角大小的平面角是关键,但同时要让学生自己去发现,发现定义的同时要发现定义的本质,知其然知其所以然.
师:既然二面角有大小也可以用平面角来度量,那么,请大家拿出教科书,并把它合成30°的二面角.
同学纷纷拿出书本,大部分同学基本上能感性的感觉出二面角平面角的初步思维,并比划这个30°角,如图2所示.

图2

图3
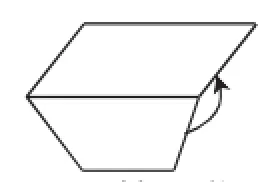
图4 某同学残缺的书页
师:平面角的定义?
学生:一个顶点出发的两条射线所成的几何图形.
此时很多同学陷入了思考,感觉可望不可及.几分钟以后,大部分同学都能用手指出如图3所示,接下来却发生了一个小意外.我发现中间位置的几个学生在激烈的讨论,问其原因,原来其中的一个学生的一页书是残缺的,而他始终认为边缘的这个角就是二面角如图4.
于是我就顺着学生的意思,将错就错索性向同学借来一把剪刀把刚才硬纸板的二面角剪成如图5所示的图形,也残缺.过程如下:
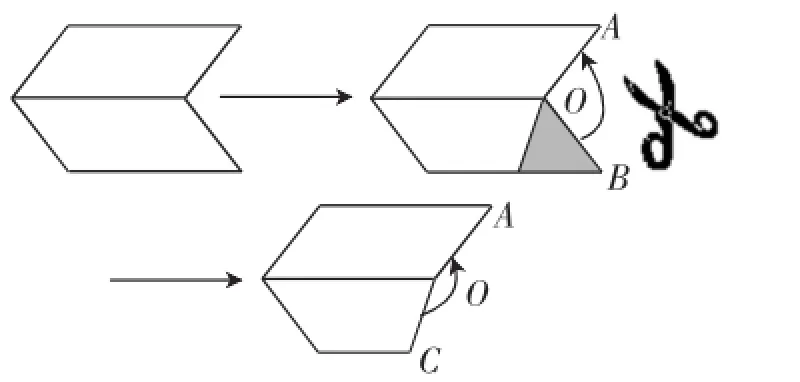
图5
2.相互讨论,“剪”出定义
剪掉以后,大部分同学开始茫然,在没有给出二面角平面角定义的前提下,如何寻找到这个角确实有很大的困难.根据课后小调查如下:

赞成反对认为∠AOB100%0认为∠AOC40%50%
除了一些人犹豫不决以外,还有多同学认为是∠AOC的.
师:能否用一个角来度量二面角的大小,关键在于此角具有唯一性,∠AOC可以吗?
生甲:显然不可以,就像直线和平面所成的角一样,我们所找到的这个角必须具有唯一性,因为唯一才能确定.如果∠AOC可以,那么再剪一点进去的∠AOD也可以的,有∠AOE,∠AOF等等.
生乙:不是∠AOC,因为这个角的两边与棱不成等角,不能唯一确定.
师:那我们能否按如图6所示的剪?另一个半平面也剪掉,与棱成等角,如图6.
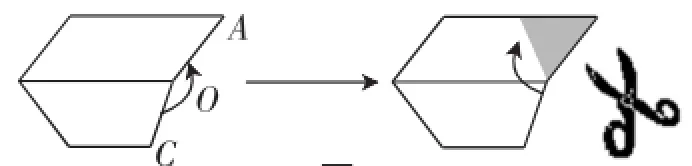
图6
生丙:其实剪的时候,等角是前提,我们能不能用剪刀平行地剪下去呢?如图7.

图7
师:同学甲分析得很有道理,要确定和唯一.而乙同学和丙同学所剪这只角本质是一样的,只具有确定性,不具有唯一性,那么请同学再思考一下,有没有办法再用剪刀剪出一个二面角的平面角呢?
生丁:要做到唯一,必须等角;要做到确定,等角须是直角.所以角的两边都在两个半平面内,并且两条射线都垂直于棱就可以了.故只要剪刀垂直于棱剪下去就可以.
如此一来,大部分同学既能理解二面角的平面角的定义,又能作出简单二面角的平面角.此外剪刀可以看成一个平面,二面角的平面角就相当于用一个垂直于棱的平面去截,所得的一个平面角,并且得到二面角平面角的特征:(1)平面角的两条射线都在两个半平面内;(2)都垂直于棱.
二、过程简析,余音绕梁
1.在生活中探索,感性认识上升到理性认识,培养学生探索思维
二面角在生活中是常见的,缓慢打开教室的门,门与墙面之间要形成一定的角度,修筑水坝时,为了使水坝坚固耐久,必须使水坝面和水平面成适当的角度等.但这些只是初步的感性认识,往往很多学生会认为这些问题很简单,但经过启发暴露问题的同时也提升了自己的认识.所有成功的理念都来源于最初的感性的想法,数学是基础学科,最基础的往往是最枯燥的.而笔者认为,要使学生获得在数学学习上持久的动力,则必须使学生喜欢数学,对学习数学有自信心和兴趣.本案例就是从学生动手、探索角度为切入点,使学生从“要我学”到“我想学”,不仅会学数学,而且“享受数学”,不仅学到了数学知识,而且培养了“数学审美”,整节课都围绕二面角平面角的定义展开,通过探索-实验-再探索-再实验-得到正确的结论,学生完成一个完整的知识建构过程.
2.在错误中探索,在尝试错误中前进,促进学生的全面发展
桑代克是美国哥伦亚大学心理学教授,被认为是联结学派的首创者,他做过“饿猫开门取食”实验,饿猫在笼里乱咬、乱撞,最后偶然打开门,取得食物.在尝试过程中,错误的反映逐渐减少,正确的反映逐渐增加,最终形成固定的反映.在授课过程中,学生的反映很多的时候是错误的,比如上文提到的如何剪出二面角以及二面角的唯一性,都有错误的尝试,摸着石头过河,最终就能到达对岸.
在对二面角平面角定义以后,说明定义合理性、唯一性、确定性时.学生丙提出能否用与棱都成等角的两条射线定义二面角?如图8.
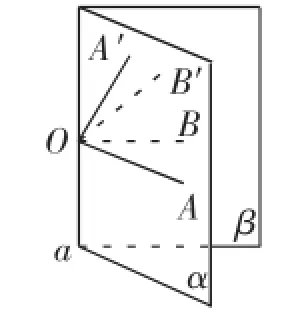
图8

图9
我们知道根据等角定理,∠A′OB′是存在也唯一的.但我们用刚才的剪刀去剪出这个二面角平面角的时候,我们是定义垂直于棱,根据刚才的这位同学的意思,就是剪刀不与棱垂直可以吗?不行,第一,它与实际情况不附,如图9,当两平面垂直时,φ≠90°,第二,如图9,我们用剪刀剪出两个等角,设∠A′P′B′=θ,∠A′PB′=φ,A′P′= a,A′P=b,A′B′=x,由余弦定理,得
x2=b2+b2-2b2cosφ=2b2(1-cosφ),x2=a2+a2-2a2cosθ= 2a2·(1-cosθ),所以.在RT△A′PP′,sin=.假设φ为二面角的平面角,可以知道,两个变量之间有一定的联系,故如此定义不够简洁,也不够科学.整个过程向学生充分展示了思维的形成过程,让学生亲身体验到发现问题、解决问题的思维过程.通过数学小实验:剪纸,而在具体剪的过程的中有很多错误的剪法,在很多错误的剪法中寻找唯一正确的剪法,不仅是学生学习数学知识的认识活动和实践过程,更大程度上是培养学生理念、科学的学习态度,合作学习精神的过程.通过“学”和“做”的整体活动,激发学生的学习兴趣,培养学生的注意力、意志力.
本节课在意外的情况下获得了意外的收获,但其意义远不止于此,对以后的教学有着深远的影响.学生的想法永远是最初的想法,在“传道、授业、解惑”中把握学生那些意外的最初的想法才能真正把握学生,让学生能成为课堂,以至整个学习的主体,而这也是新课程要求和倡导的.让学生去探索,教师自己必须具有创新精神,我们不应该将学生的思维强行引入自己的思维模式,我们启发的目的不是求同,著名的数学教育家波利亚曾说过“中学教师在课程知识获得方面最大的缺陷正是主动完成数学工作的独创性经验”.追求探索,不是“胡思乱想”,但应该提倡“异想天开”,敢于质疑,善于求异,是创新的基本品质.“我探索,因为我志在探索,我创新,因为我志在创新”.让这些意外最终不意外.
1.中华人民共和国教育部.普通高中数学课程标准(实验)[M].北京:人民教育出版社,2003.
2.罗增儒.中学数学课例分析[M].西安:陕西师范大学出版社,2003.
3.郑毓信.数学文化学[M].成都:四川教育出版社,2000.
4.罗增儒.数学理解的案例分析[J].中学数学教学参考,2003(4).
5.黄新民.初中数学课堂创新教学理论与实践[M].杭州:浙江大学出版社,2002.
6.朱哲,张维忠.一节基于数学史的教学课例:正四棱台的体积公式[J].中学数学教学参考,2004(3).那么为什么会出现上述的错解,我们还是要来分析一下原因,避免下次再犯类似的错误.对于基本不等式a+b≥ 2(a>0,b>0),若2为定值记作m,则对于任意的a>0,b>0,都有a+b≥m且存在a=b时a+b=m,这时候我们可以说m即2是a+b的最小值,若2不是定值时,同学们还认为就是在a=b时取到a+b的最小值2,就会出现错误了,虽然a+b≥2( a>0,b>0)这个不等式还是存在,但是2现在是一个不断变化的量了,所以有可能会出现比a=b时更小的a+b.例如:若a=x+1,b=2x,则当a=b,即x+1=2x(x=1)时,a+b=2=4,利用一次函数的最值我们很容易看出应该是当x=时,a+ b=3x+1取到最小值.
设计思路:这种错误也是这类最值问题中比较常见的类型,如果只是让学生死记硬背“一正,二定,三相等”,一来是学生印象不深,容易忘记,二来也不够具有说服力,只有从本质上指出学生错误的根源,即对最值概念的理解及对基本不等式的理解不够透彻,提出来并解释清楚才能让学生信服并真正理解.
在上述纠错过程中我们可以发现,只有基于概念和知识本质去探究“为什么错”,才能抓住问题的本质,不只是训练解题的机器,而是切实提高学生的数学素养,培养学生一直受用的方法和能力.
三、思考
最后,笔者谈谈自己对如何在日常教学中提高学生数学素养的几点想法:第一,数学素养对学生的数学学习起着决定性作用,因此,在教学中关注学生数学素养的提高至关重要,执行刻不容缓;第二,在数学教学中提高学生的数学素养是一项长期而系统的工作,不可能一蹴而就;第三,教师努力提高学生的数学素养的前提是需要自身具有较高的数学素养,因此,教师自己首先需要多学习多研究,遇到问题多挖掘其本质.
参考文献:
1.水菊芳.就“映射”教学谈学生数学素养的提高[J].中学数学教学参考(上),2015(10).
2.王峰.基本不等式法求最值的一个教学困惑[J].中学数学教学参考(上),2015(4).
3.郑良.立足理解数学促进数学理解[J].中学数学教学参考(上),2015(8).F

