圆锥曲线综合题破障的通法及应对策略



圆锥曲线综合题破障的通法及应对策略

福建省邵武市第四中学(354000)刘会彪

圆锥曲线是解析几何中重要一章，圆锥曲线综合题集函数、方程、不等式、数列、向量等众多的知识点，是函数与方程思想、数形结合思想、化归转化思想、分类与整合思想的重要载体.形数连结，关系错杂，变量众多，计算繁琐，有思路没出路，有想法没办法，有的考生解此类题畏缩不前，退避三舍或避重就轻.如何打通圆锥曲线综合题解题障碍的“任督”二脉？波利亚在《怎样解题》给出解题四个步骤：弄清问题，拟定计划，实现计划，回顾.考纲提出 “淡化特技，强调通法”，结合多年的教学实践，基于圆锥曲线的特点，寻求常规下‘自然地’‘清楚地’解决这一问题‘细化’的方法和策略，从模型化、系统化、算法化地角度思考，笔者提出——突破圆锥曲线综合题解题障碍的通性通法：阅读理解→数形结合→选择变量→寻求关系→消参转化→解题反思.以及解题过程中产生相应策略：数形策略、动静策略、特殊一般策略、整体局部策略、转化代换策略、主元策略、反思策略.现以2015年课标Ⅱ卷理数第20题为例，加以说明.

问题已知椭圆C:9x2+y2=m2(m>0),直线l不过原点O且不平行于坐标轴，l与C有两个交点A，B，线段AB的中点为M．

(Ⅰ)证明：直线OM的斜率与l的斜率的乘积为定值；

一、审题闯关，全方理解，以形助数

解析几何核心思想应是数形结合思想.美国科学家斯蒂恩说：如果一个特定问题可以被转化为一个图形，那么思想就整体地把握了问题，并且能创造性地思索问题的解法.从画图入手，图文并茂，培养学生基本画图能力，以形助数；学会观察图形，深入分析图形中几何特征，把解题动态情境过程形象化，寻求解题的突破口.

障碍1方程含参，形动不定，怎么画图？

破障1策略：以静制动，特殊代一般.可令m=3，作出图形1.

障碍2问题(Ⅱ)隐性的条件直线l的斜率k范围怎么挖掘？

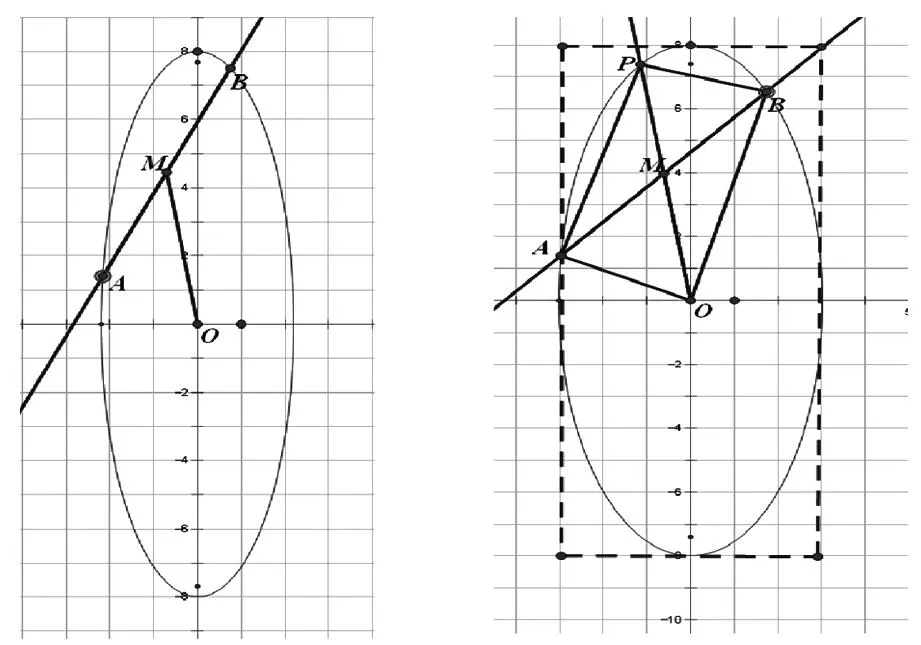
图1　　　　　　　　　图2

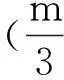
二、局部入手，几何审视，动静搭配

所谓解析几何，就是‘几何’解析，也就是用代数方法研究几何问题.圆锥曲线综合题应遵循‘代数化’的思路，从局部几何元素入手，把几何条件‘翻译’成代数方程处理，再构建解题思路.

几何条件几何问题代数化元素分析代数分析关系分析椭圆C直线l两个交点A,B线段AB的中点M点(m3,m)线段OM与C交于点P四边形OAPB为平行四边形C:9x2+y2=m2(m>0)l:y=kx+b(k≠0,b≠0)A(x1,y1)、B(x2,y2)M(xM,yM)k>0,k≠3xM=XP+XO2yM=yP+yO2ìîíïïïïy=kx+b9x2+y2=m2,△>0{x1+x2=-2kbk2+9xM=x1+x22,yM=kxM+bkOM=yMxMy=-9kx9x2+y2=m2{xP=2xM

分析以上已知条件，设计解题思路，思维导路图如下表：

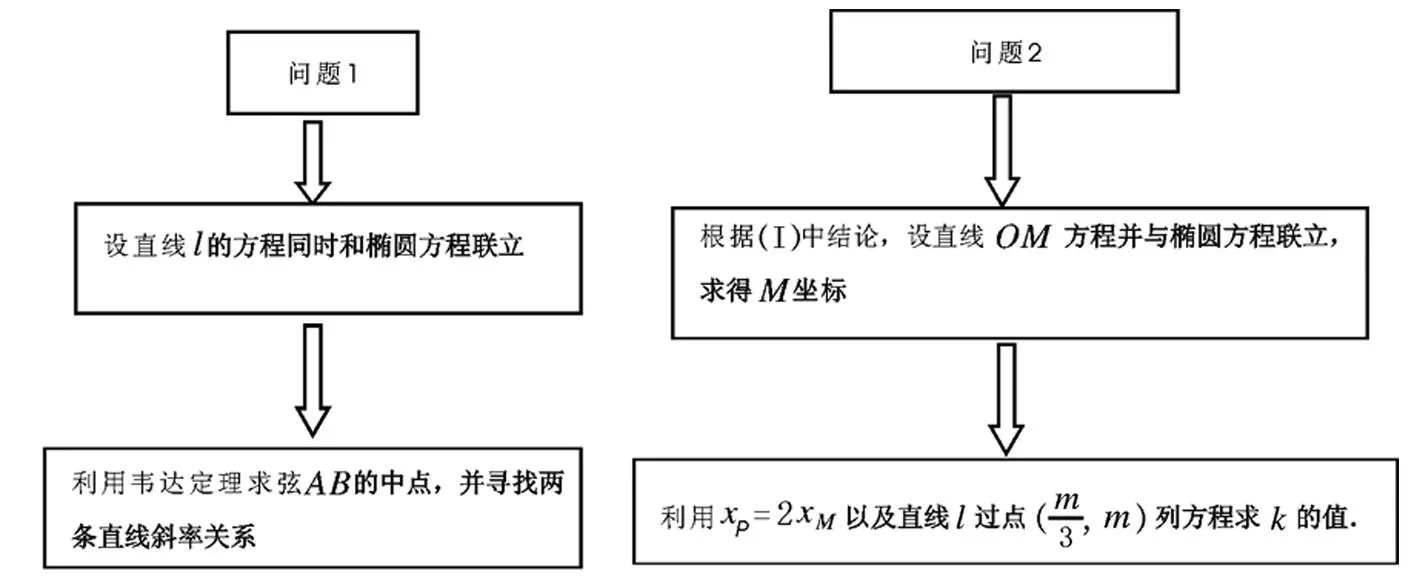
三、整体思维，突破运算，设而不求

运算能力包括分析运算条件、探究运算方向、选择运算公式、确定运算程序等一系列过程中的思维能力，也包括在实施运算过程中遇到障碍而调整的运算能力.有的考生生搬硬套公式不能灵活地对式子结构进行合理变形；有的考生‘只顾埋头拉车’——盲目地推理演算，‘不抬头看路’—— 缺乏运算目标和方向；有的考生运算过程繁琐，不会选择合理、简洁的计算方法或规避繁琐讨论，大部分考生对整理、及时化简、讨论能力较差，暴露出考生运算能力差，特别是含有字母的运算变形不过关的现象.有待于训练强化，突破‘瓶颈’.

障碍3直线方程多样，变量众多，如何选择？

破障3策略：选择方向，主元策略，减元消参.

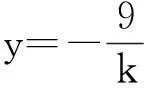
障碍4‘设而不求’带来的困惑.

破障4策略：寻求目标、整体代换，消参转化.

四、解题反思、一题多解、变式拓展

波利亚说过：“数学问题的解决仅仅只是一半，更重要的是解题之后的回顾.”回顾就是反思.反思什么？怎么反思？能否把问题的本质进行深入地探究？能否把‘孤立的点’拓展到‘系统的面’？ 能否拓展推广？能否一题多解？是否优解？是否简解？考虑问题是否严密？条件有否缺失？多角度、多途径展开思维.前面的上述问题限于篇幅，请读者不妨打开思路，也可用点差法试一试.

(Ⅰ)直线OM的斜率与l的斜率的乘积是否为定值？

题后话波利亚认为：解题活动‘决心’和‘情绪’所起作用很重要.匈菲尔德强调数学解题需考虑四个要素：知识基础、解题策略、自我控制、信念基础.在解题过程中要坚定信心、敢于尝试、迎难而上，独立思考，自主探索，调整心态，调动非智力因素，锻炼自己的意志品质，圆锥曲线有险阻，攻题破障不畏难.圆锥曲线综合题破障的 ‘通法’只是解决某一模式数学问题的方法，并非‘放之四海而皆准’的万能方法，也不是‘剑走偏锋’的特技，应了解解题方法的来龙去脉，理解更一般性的数学思想和策略，这样，在考试中才能立于不败之地.

参考文献

[1]白雪.落实三个抓手突破直线和圆锥曲线综合题[J].《高考》理科版，2010,12,26-28.

[2]张益红.例谈解析几何综合题的解题策略[J].中学数学教学,2010,2,33-36.