复合材料胶接修补结构有限元分析方法研究

韩 允， 刘元海 ， 肖晓晖

(1.武汉大学,湖北 武汉 430080；2.海装武汉局，湖北 武汉 430080；3.中国特种飞行器研究所，湖北 荆门 448035)

复合材料胶接修补结构有限元分析方法研究

韩 允1,2， 刘元海3， 肖晓晖1

(1.武汉大学,湖北 武汉 430080；2.海装武汉局，湖北 武汉 430080；3.中国特种飞行器研究所，湖北 荆门 448035)

以铝合金裂纹板和T300/E51复合材料单边胶接修补裂纹板静力试验结果为基础，建立了适合模拟J-150胶层的“双板-弹簧元”有限元分析模型，并用于其它多种复合材料胶接修补设计方案的静强度评估分析，能够很好地再现试验结果。该有限元分析方法的提出可用于指导金属损伤结构复合材料快速修补方案的优化设计。

复合材料；胶接修补；有限元；双板-弹簧元；破坏强度

0 引言

理论分析是金属损伤结构复合材料胶接修补件设计的主要手段。通过理论分析、数值计算，可以用较小的费用，获得修补设计的强度分析结果，节省时间，保证进度。近年来，随着计算机计算速度的不断提高和计算规模的不断扩大，有限元分析方法的应用范围越来越广，有限元方法对修理结构件的形状和补片的铺层没有限制，且计算精度较高，已成为复合材料胶接修补结构强度计算的首选方法[1-6]。

金属损伤复合材料修补结构件的有限元求解的难点是必须借助试验数据确定模型相关参数。因此，本文以铝合金裂纹板和T300/E51复合材料单边胶接修补裂纹板静力试验真实数据为基础，建立“双板-弹簧元”有限元计算模型，同时应用该模型对多种复合材料补片胶接修补结构静强度进行了评估分析，验证了模型的正确性。

1 有限元分析模型

1.1 基本计算假设

通常情况下，对于平面薄板上的穿透型裂纹问题，采用二维分析模型就可以获得较高的计算精度，并可减少计算时间和计算费用。因此，在本文的分析计算中，含裂纹金属母板和复合材料补片均采用平面有限元分析单元。

为了便于分析计算，根据胶接修补结构的实际情况，作如下基本假设：

1) 金属裂纹板和复合材料补片的厚度与各自的面内尺寸相比很小，均处于平面应力状态，且限制在线弹性变形范围内；

2) 胶层为各向同性材料，且只考虑其剪切变形；

3) 初始胶接质量完好，没有任何形式的损伤；

4) 在单面胶接修补中，不考虑因结构不对称而引起的弯曲变形。

1.2 几何参数

根据中心裂纹试样的几何尺寸(如图1)建立二维有限元计算模型，使用的承载试样为LY12CZ铝合金板，板长260mm，宽70mm，中间段宽60mm，厚度为2.8mm。粘胶为J-150胶，厚0.1mm。补片材料为T300/E51层合板，单层厚度为0.14mm。

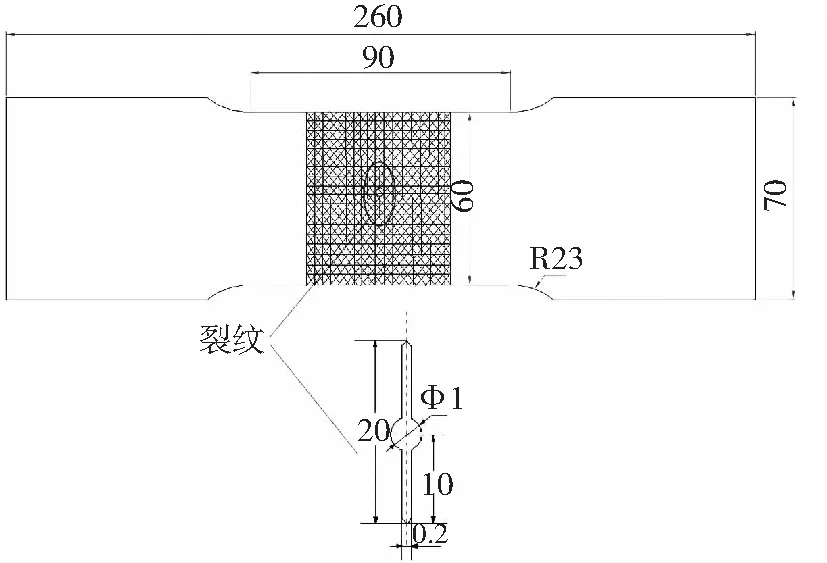
图1 计算模型的几何形状和尺寸

1.3 材料性能

计算模型材料包含铝合金板、T300/E51复合材料补片和胶层，补片铺层角为0°/45°/-45°/90°(0°铺层角纤维方向平行于载荷方向或垂直于裂纹方向)。三种材料性能参数均为试验测试值，具体参数见表1。

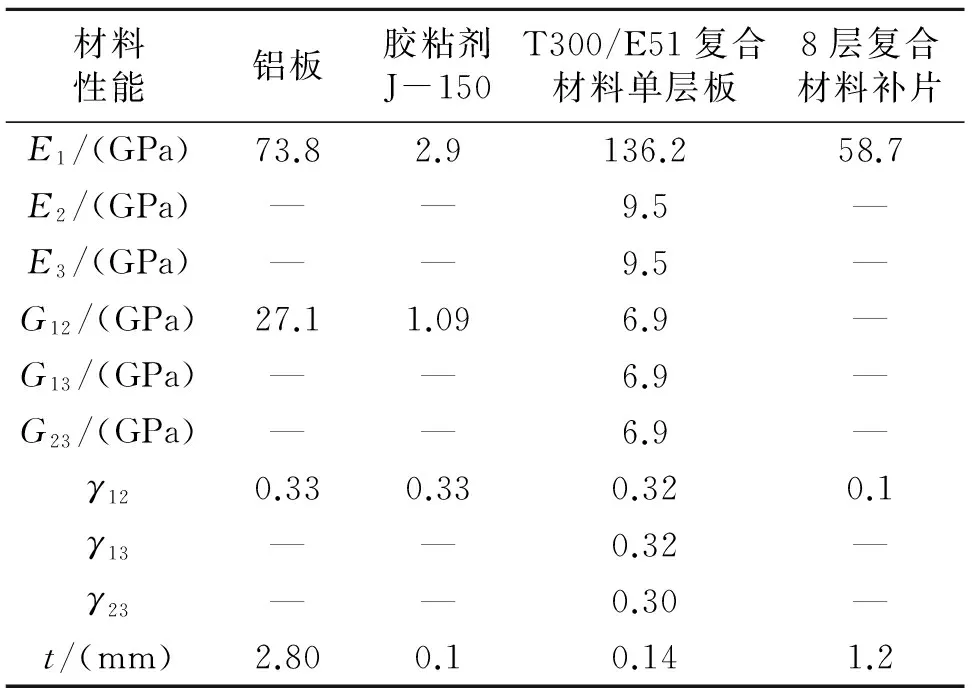
表1 计算模型所用材料性能参数

1.4 有限元分析单元

考虑到复合材料补片的准各向同性，本次有限元分析中，裂纹板和补片均采用4节点板单元，在裂纹尖端采用加密网格。其中，铝合金裂纹板件共有8144个单元，8864个节点，补片上单元和节点与裂纹板对应区域完全一致。铝合金裂纹板和复合材料补片之间的胶层采用“弹簧元”模拟，弹簧元上下两个节点分别位于裂纹板和补片上，如图2所示。

图2 “双板—弹簧元”模型

1.5 有限元分析模型的确定

为建立可靠的“双板-弹簧元”有限元计算模型，首先按1.2节所述的金属裂纹板和复合材料补片几何参数制备试验件，开展了表2所列30件试验件的静力拉伸试验(试验结果见表3)，为计算模型的确定及验证提供数据支持。

由试验结果可知，采用T300/E51复合材料补片和J-150胶粘剂修补的铝合金损伤件在静拉伸载荷作用下的失效/破坏均是金属裂纹板主导的破坏。因此，在有限元分析中，将金属损伤件的承载情况或应力分布情况作为复合材料修补件失效的主要判据。

以表3中未修补金属损伤试件和单面复合材料修补试件(60×60×1.2)静力破坏载荷为基础，通过调整“双板—弹簧元”模型中的弹簧元刚度系数(K)，确保单面复合材料修补件在试验破坏载荷P2=61.8kN作用下的裂纹尖端应力分布情况等于/尽可能接近未修补金属损伤件在破坏载荷P1=42.7kN作用下的裂纹尖端应力分布情况，建立适用于J-150胶层的“双板—弹簧元”模型。

通过多次尝试性计算可知，当采用刚度系数K=265kN/m的弹簧元构建的“双板-弹簧元”模型模拟金属-复合材料修补件时，单面复合材料修补件在试验破坏载荷P2=61.8kN作用下的裂纹尖端应力分布情况(见图3)最接近于未修补金属损伤件在破坏载荷P1=42.7kN作用下的裂纹尖端应力分布情况(见图4)。因此，拟用该模型于其它修补方案的验证计算。

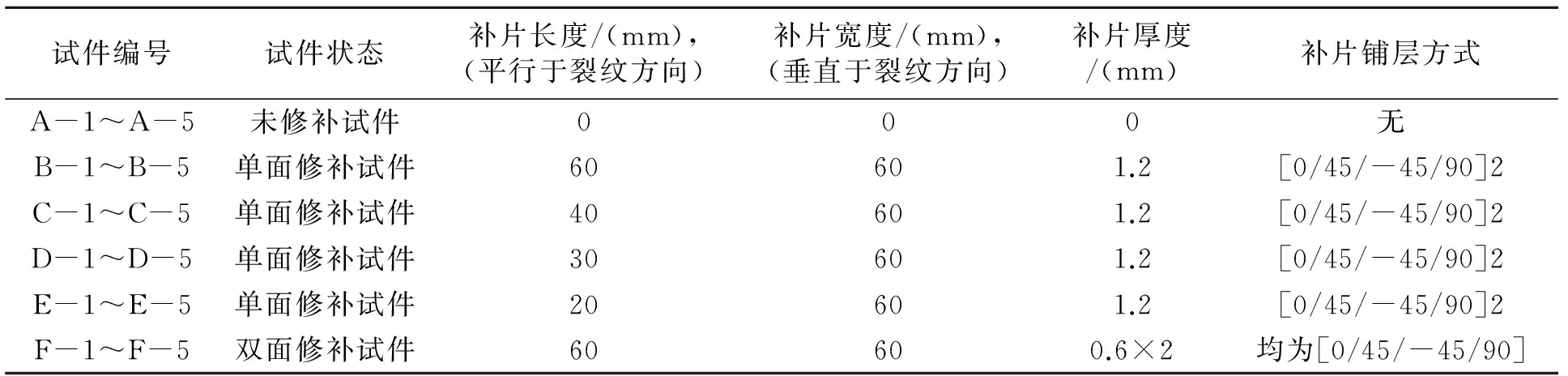
表2 试验件的分组及补片方式

表3 试验件拉伸强度试验结果

图3 复合材料单面修补损伤板应力云图图4 未修补金属损伤板应力云图

2 复合材料修补件有限元分析模型的应用与验证

采用弹簧元刚度系数K=265kN/m的“双板-弹簧元”模型模拟金属-复合材料修补件，对金属损伤件其它修补设计方案(单面修补(不同补片长度：40×60×1.2,30×60×1.2,20×60×1.2),双面修补(60×60×0.6))的破坏强度进行计算，并与试验结果对比分析，考察模型的有效性。

计算时，在未修补金属裂纹板拉伸破坏载荷的基础上，设置外载荷增幅，逐级增加载荷，并在各级载荷作用下进行金属损伤件应力状态分析。

计算结果显示，当40×60×1.2,30×60×1.2,20×60×1.2复合材料单面修补件及60×60×0.6复合材料双面修补件的作用载荷分别为54.0kN、51.7kN、48.2kN和72.2kN时，各修补裂纹板中的应力分布情况均与未修补金属裂纹板在破坏载荷作用下的应力分布基本一致，裂纹尖端最大应力值均为σmax=1450MPa。因此，40×60×1.2,30×60×1.2,20×60×1.2复合材料单面修补件及60×60×0.6复合材料双面修补件的静力拉伸破坏载荷计算结果分别为54.0kN、51.7kN、48.2kN和72.2kN，其与表3中试验结果的对比见图5。

图5 破坏载荷计算结果与试验结果比较

由图5可知，四种不同修补设计方案静强度计算结果与试验结果基本吻合，最大绝对偏差4.6kN(8.7%)，最小绝对偏差仅为0.6kN(1.1%)。其偏差主要来源于实际工况的假设处理以及试验误差等。

理论计算结果的精确性是体现模型的科学性/可靠性的一方面。同时，就4种单面修补设计方案(包括60×60×1.2单面复合材料修补试件)单独考虑，随补片宽度的减小(60mm→40mm→30mm→20mm)，复合材料补片上应力值(尤其是裂纹上部

复合材料补片区域)逐渐减小(最大应力从262KPa减至99.1KPa)，复合材料补片分配/传递的载荷相应逐渐减小，可见“双板-弹簧元”模型中刚度系数为K=265kN/m的“弹簧元”起到了良好的剪切传递载荷作用，也体现了模型的合理性。

3 结论

1)以未修补金属损伤件和复合材料单面修补件静力试验结果为基础，可建立适合J-150胶层的“双板-弹簧元”有限元分析模型。

2)所形成的模型方法可较好地指导复合材料修补结构(T300/E51复合材料补片和J-150胶粘剂胶接修补金属损伤结构)的静强度设计。

3)本有限元分析方法/模型的建立，为采用其它胶接修补材料(补片和胶粘剂)、修补方案(补片形状、尺寸、厚度等)修补的金属损伤结构的优化设计提供了新思路。

[1] 刘艳红,等.复合材料补片胶接修补结构的有限元分析[J]，中国名民航学院学报，2000，18(6)：13-16.

[2] Jones R，Callinan R J. Finite Analysis of Patched Cracks[J].Journal of Structure Mechanics，1979，7(2)：107-130.

[3] Chandra R. Numerical Estimation of Stress Intensity Factors in Patched Cracks Plates[J].Engineering Fracture Mechnics，1987(27)：559-569.

[4] 王必宁.复合材料胶接修补金属裂纹板的计算与试验研究[D].西安：西北工业大学，2004.

[5] 孙洪涛.损伤金属板复合材料胶接修补的热-力分析与试验研究[D].西安：西北工业大学，1998.

[6] 孙洪涛, 刘元镛, 彭 俊. 复合材料胶接修补问题的试验研究和分析[J]. 实验力学, 1999, 14(4): 419-424.

Finite Element Analysis of the Structure Bonded with Composite Patches

HAN Yun1,2, LIU Yuanhai3, XIAO Xiaohui1

(1.Wuhan University, Wuhan 430080, China;2.Wuhan Military Representative Bureau of Navy Equipment Department, Wuhan 430080, China;3.Institute 605th of Aviation Instrument of China, Jingmen 448035, China)

J-150 “double-plate-string-element " finite element analysis model was established on the basis of static test results from aluminum alloy cracked plate and T300 / E51 composite bonded cracked plate. The model was also used to assess and analyze static strength of many other composite patch repaired strategies with a good reproducibility, which can be used to optimize the design of damaged metal structure fast repair by bonded composite patches.

composite material; bonded repair; Finite Element; double-plate-string-element; breaking strength.

2016-06-02

韩 允(1982-)，男，工程师，武汉大学机械工程专业硕士在读，研究方向：机械设计及理论。

1673-1220(2016)03-032-04

V267+.46

A