直升机高原环境飞行性能计算方法研究

徐自芳，洪永军，朱清华

(1.中国直升机设计研究所，江西 景德镇 333001；2.南京航空航天大学，江苏 南京 210016)

直升机高原环境飞行性能计算方法研究

徐自芳1，洪永军1，朱清华2

(1.中国直升机设计研究所，江西 景德镇 333001；2.南京航空航天大学，江苏 南京 210016)

提出了一种适合高原的高精度直升机飞行性能计算方法。首先建立全机气动力模型，并进行飞行动力学建模，计算了全配平姿态的需用功率；再分析了发动机功率高度温度特性模型和耗油率高度温度特性；最后验证方法的有效性和精度性。

高原；飞行性能；高精度；计算方法

0 引言

我国地形复杂，雪灾、地震等自然灾害频发，雪域高原地带尤为显著，直升机以其垂直起降、空中悬停等优势在紧急救援任务中发挥着至关重要的作用。高原环境飞行，特别是在我国的青藏高原飞行，具有温差大、气压低、空气密度低等特点，对直升机的飞行性能提出了严峻考验。

直升机飞行性能主要取决于飞行时直升机需用功率和发动机可用功率。常规的直升机飞行性能计算[1]采用简化的滑流理论和叶素理论，仅计算旋翼桨叶特征剖面的气动力，且不考虑气动干扰，仅简单地配平直升机飞行姿态，同时发动机功率和耗油率的高度温度模型也较为粗略。

为了建立适合高原的高精度直升机飞行性能计算方法，本文首先利用叶素积分法计算旋翼需用功率，并考虑高原地区空气低密度对直升机桨叶翼型气动特性的影响，机身姿态角对需用功率的影响及旋翼对机身、平尾等的气动干扰，进而建立高精度的适合高原飞行的直升机需用功率计算方法。然后考虑高原高度温度对直升机发动机的影响，建立适合直升机高原飞行性能计算的发动机功率高度温度特性模型和耗油率高度温度特性模型，以用于直升机飞行性能计算中的可用功率的计算。

1 需用功率

对于单旋翼直升机，其水平飞行时的需用功率包括旋翼、尾桨、附件设备(液压泵、电机等)需用功率和传动系统功率损失等。旋翼、尾桨功率按照下述方法计算，附件设备需用功率和传动系统功率损失按占全机需用功率的5%计算。

1.1 全机气动力

1.1.1 旋翼

叶素相对气流的切向速度UT、垂向速度UP和径向速度UR分别(如图1所示)为：

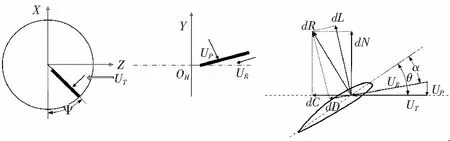
图1 桨叶剖面受力及来流速度UT、Up和UR示意图

其中，vX、vY、vZ分别为飞行速度在X、Y、Z三个轴方向的分量，β和ψ分别为桨叶挥舞角和方位角。vi为旋翼诱导速度，可以通过式(4)计算取得：

式中：λ0、λS和λC分别为入流常数项、正弦项和余弦项，通过应用Pitt-Peters[2]动态入流理论计算得出。

挥舞响应采用韦恩·约翰逊[3]的经验方法计算。

叶素迎角表达为：

式中，θ0为总距角，θtw为负扭角，A1S和B1s分别为纵、横向周期变距。

根据桨叶翼型升阻特性数据，即α-Cl及α-Cd关系，由得到的α值，计算翼型升力系数Cl和翼型阻力系数Cd值，然后可以计算出叶素升力和阻力为：

由式(6)、(7)计算出单片桨叶的升力和阻力，然后按坐标分解，积分求出整个旋翼的气动合力和力矩。以式(8)可以求解出旋翼的扭矩：

式中，Kb为桨叶片数，e为挥舞铰偏置量，b为桨叶弦长。

扭矩乘以转速就可以得到旋翼需用功率。

考虑到直升机高原飞行时，随着飞行高度的增加，空气密度降低，同时高原具有较高的温度，故而直升机旋翼翼型工作的雷诺数较在平原飞行时更低，因此，需要考虑低雷诺数对旋翼翼型升力阻力特性的影响，在计算旋翼叶素升力阻力时需要对影响翼型升阻系数进行雷诺数修正。

雷诺数计算如下：

其中：ρ为大气密度，b为桨叶弦长，Ω为旋翼角速度，V为前飞速度，μ为大气粘性系数。

1.1.2 尾桨、平尾、垂尾、机身

尾桨的气动力建模采用叶素理论，具体方法与旋翼类似。

平尾气动力模型按如下方法建立。假设平尾气动压力中心与全机重心的距离在横向、纵向方向上分别为ls、hs，则平尾动压如公式：

平尾迎角：

则平尾所产生的气动力为：

式中，u，w为全机气动压力中心处水平方向、垂向上的速度分量；SS为平尾的面积；CLs，CDs分别为平尾的升力系数和阻力系数。uHR,I，wHR,I为旋翼在平尾处水平方向及垂向的干扰速度，这些参数的确定参照后文建立的气动干扰模型。

垂尾气动力建模方法与平尾类似。

机身阻力通常通过试验吹风获得。

1.1.3 气动干扰

直升机在进行飞行性能计算时，大多没有考虑各部件之间的气动干扰。这些干扰主要包括旋翼对机身、平尾、垂尾的干扰，尾桨对垂尾的干扰以及机身对平尾和垂尾的干扰等。本文在考虑直升机气动干扰问题时忽略机身对各气动部件的影响，主要考虑旋翼对机身、平尾的下洗效应，还有垂尾对尾桨的阻塞作用。

旋翼对机身的干扰主要影响低速飞行时的性能，特别是悬停状态。因为在低速时，旋翼的诱导速度大，它在机身上作用较大的向下气动载荷，使旋翼拉力增加。本文借鉴黑鹰直升机旋翼对机身的干扰数据，假设旋翼对机身、平尾的干扰因子随尾迹倾斜角的变化趋势如图2所示，能大致反映干扰作用的变化趋势，它是旋翼诱导速度和旋翼尾迹倾斜角的函数。

直升机垂尾对尾桨的阻塞因子随前飞速度的变化如图3所示。在直升机小速度前飞时，直升机垂尾对尾桨存在一定的阻塞作用，随着速度的增加，阻塞作用减小，当达到一定的速度后阻塞作用近似可以忽略。

图2 旋翼下洗干扰

1.2 全机配平

直升机的姿态，特别是前飞时的机身俯仰姿态对机身的气动力、旋翼的操纵有着较大的影响，进而对直升机飞行时的废阻功率产生影响，因此，为了提高飞行性能计算精度，飞行性能计算方法中需要进行直升机飞行配平，特别是前飞时的纵向状态配平。

直升机稳定飞行时，必定处于平衡状态。在此状态下，处于通过直升机重心的体轴坐标系OXYZ中的三个轴力以及绕轴作用的三个力矩都是平衡的，包括作用于直升机的气动力和重力，如图4所示。

图3 垂尾对尾桨的阻塞作用

图4 平衡时体轴系中作用在直升机上的力和力矩

由刚体运动平衡条件，可得到如下六自由度非线性的直升机平衡方程组[4]：

∑Fx(θ0,A1S,B1S,φT,γ,ϑ)-mgsinϑ=0

∑Fy(θ0,A1S,B1S,φT,γ,ϑ)-mgcosϑcosγ=0

∑Fy(θ0,A1S,B1S,φT,γ,ϑ)+mgcosϑsinγ=0

∑Mx(θ0,A1S,B1S,φT,γ,ϑ)=0

∑My(θ0,A1S,B1S,φT,γ,ϑ)=0

∑Mz(θ0,A1S,B1S,φT,γ,ϑ)

求解时，气动力及力矩由上述的全机气动力模型提供，给定飞行状态参数，经过求解可以得到直升机稳定飞行时的四个操纵量θ0,A1S,B1S,φT,即：总距、横向周期变距、纵向周期变距和尾桨距，两个姿态角γ,ϑ,即：滚转角和俯仰角，同时可以计算出配平状态下的旋翼、尾桨的需用功率。

2 发动机功率与耗油特性

2.1 发动机和耗油率的高度温度特性

在直升机飞行性能计算时，常常缺少直升机发动机的功率耗油率的高度温度特性数据，或者计算时所给的高度温度特性数据的范围较小。为了更加精确地计算发动机的可用功率和实际耗油率，可以根据发动机的工作特点，建立不同高度温度时发动机可用功率和耗油率与标准状态值之间的关系，这样就可以计算不同高度温度时发动机的可用功率和耗油率。

直升机发动机可用功率和耗油率的高度温度特性如下：

其中：SHP0、SFC0分别为海平面标准大气时发动机的可用功率和耗油率；SFC、SHP分别为标准状态时发动机耗油率和可用功率。δ、θ分别表示大气与海平面标准大气的压力比和温度比，即：

考虑不同功率状态时，发动机的耗油率也不相同，可以根据以下公式计算发动机不同功率状态时的耗油率：

(19)

其中：SFCpart、SHPpart分别为部分功率状态时的发动机耗油率和可用功率。

2.2 飞行状态与发动机功率状态的关系

从理论上讲，直升机飞行状态的设计点应该和发动机功率状态相匹配，这样,发动机和直升机才能都处于最有利的工作状态。表1给出了直升机飞行状态与发动机功率状态的对应关系。

3 算例验证

3.1 需用功率验证

为了验证本文采用的基于叶素积分法的旋翼功率计算方法，同时验证适用于高原的高精度直升机飞行性能计算所引入的全机配平和全机需用功率计算方法，本研究以UH-60A直升机为算例，验证其旋翼需用功率和前飞功率计算的准确性，计算了UH-60A前飞时的配平量和姿态值，并与NASA报告值进行对比，其结果如图5至图7所示。

表1 直升机飞行状态与发动机功率状态的对应关系

图5 UH-60A稳定前飞时总距操纵量随前飞速度的变化

图6 UH-60A稳定前飞时脚蹬操纵量随前飞速度的变化

图7 UH-60A稳定前飞时俯仰角随前飞速度的变化

从计算结果的对比可以看出本文的直升机需用功率分析模型是有效的，且计算精度较好。

其前飞需用功率如图8所示。

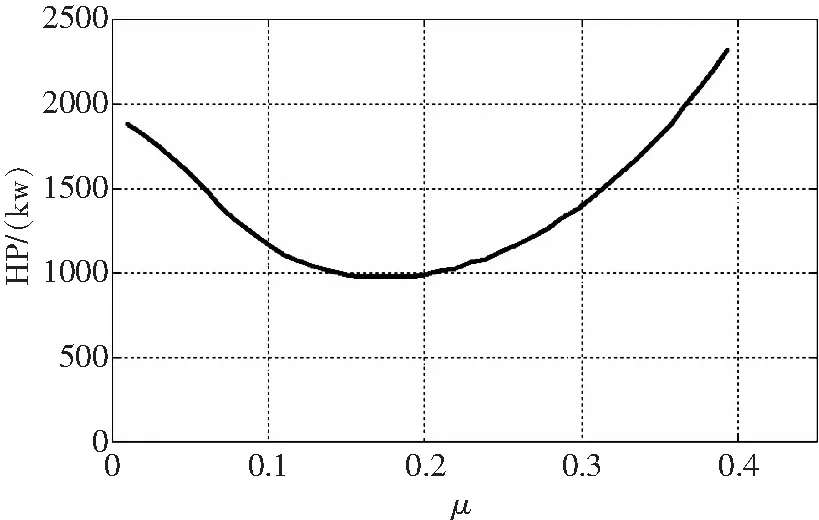
图8 UH-60A前飞需用功率图

3.2 飞行性能计算模型验证

直升机飞行性能是直升机使用技术要求的基本

指标，本研究的直升机飞行性能是指直升机常规飞行(不包括机动飞行)状态的性能，包括悬停性能、垂直飞行性能和前飞性能。

根据本文建立的直升机飞行性能分析模型，以UH-60A直升机为算例，计算其各项飞行性能，同实际飞行性能值进行比较，以验证本节建立的直升机飞行性能分析模型的有效性，计算结果如表2所示。本研究计算的UH-60A的起飞重量为7484kg，燃油重量为1060.5kg，有地效高度z/D=0.7，各项飞行性能对应的发动机功率状态、飞行高度和温度条件见表的备注，表中的各项飞行性能的实际值来自于文献[5]。

从计算结果的对比可以看出本文的直升机飞行性能分析模型是有效的，且计算精度较好。

表2 UH-60A飞行性能计算值和实际值

4 结论

通过本文的研究，可以得出以下几点结论：

1)本文根据高原的特点，提出了一种适合高原的高精度直升机飞行性能计算方法，首先从需用功率入手，在建立全机气动力模型及气动干扰模型的基础上，采用叶素理论及飞行动力学模型计算了全配平姿态的旋翼、尾桨需用功率，再由可用功率出发，建立了发动机功率高度温度特性模型和耗油率高度温度特性模型，大大提升了飞行性能计算精度。

2)本文结合算例展开计算，计算结果验证了该方法的有效性和优异性，为高原环境下的飞行性能计算提供了方法支撑。

[1] 《7210任务》办公室编．直升机气动力手册[M]．北京：国防工业出版社，1978．

[2] Pitt D M，Peters D A. Theoretical Prediction of Dynamic-inflow Derivatives[J].Vertica, 1981,5(1).

[3] Johnson W. Helicopter Theory[M].Princeton University Press, 1980.

[4] 高 正 陈仁良．直升机飞行动力学[M]．北京：科学出版社，2003．

[5] 倪先平．直升机手册[M]．北京：航空工业出版社，2003．

Research on Calculation Method of Helicopter Flight Performance for Plateau Environment

XU Zifang1, HONG Yongjun1，ZHU Qinghua2

(1.China Helicopter Research and Development Institute, Jingdezhen 333001,China；2.Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

Proposed a suitable calculation method for helicopter flight performance in plateau environment. Firstly, established aircraft aerodynamic model and flight dynamics model to give the required power based on trim state，then analyzed helicopter engine power and fuel consumption characteristics，lastly verified the effectiveness and accuracy of the method.

plateau；flight performance；high precision；calculation method

2016-05-06 作者简介：徐自芳(1992-)，女，江西景德镇人，硕士研究生，主要研究方向：直升机总体设计。

1673-1220(2016)03-001-05

V212.13；V212.4

A