基于扩展有限元法的裂纹扩展数值模拟及程序实现

崔 韦，熊 欣，喻溅鉴，王建军

(1.中国直升机设计研究所，江西 景德镇 333001；2 北京航空航天大学 能源与动力工程学院，北京 100191)

基于扩展有限元法的裂纹扩展数值模拟及程序实现

崔 韦1，熊 欣1，喻溅鉴1，王建军2

(1.中国直升机设计研究所，江西 景德镇 333001；2 北京航空航天大学 能源与动力工程学院，北京 100191)

常规有限元法在解决裂纹扩展问题时需要重构网格而使其应用受到局限。扩展有限元法(XFEM)使用扩充形函数描述不连续的位移场，具有在模拟裂纹扩展时无需更新网格模型的显著优点。基于Matlab语言实现了平面问题裂纹扩展模拟程序的开发，通过解析解算例和对某钛合金裂纹扩展试验的模拟验证了程序的精度。

扩展有限元法；裂纹扩展；数值模拟；Matlab

0 引言

疲劳引起的裂纹萌生和扩展是直升机结构失效的主要原因，近年来损伤容限设计广泛应用于直升机结构设计中[1]。常规有限元法(FEM)在模拟裂纹扩展、移动界面等不连续问题时，需要进行计算网格的重构，自动化的网格重构是困难而耗费计算资源的：一方面,全自动的网格重构无法保证全部划分结构化网格，目前计算力学界的主要策略为子模型内局部采用非结构化网格[2-4]；另一方面,网格重构将耗费较多计算资源。为了达到在模拟裂纹扩展时不进行网格重构，使用扩充形函数描述不连续位移场的扩展有限元法(eXtended Finite Element Method，简称XFEM)应运而生[5,6]。本文对扩展有限元法解决裂纹扩展问题的基本原理进行了阐述，基于Matlab语言实现了平面问题裂纹扩展模拟程序的开发，通过算例验证了程序求解应力强度因子和模拟裂纹扩展路径的精度，最后将程序用于某国产钛合金裂纹扩展试验的数值模拟。

1 扩展有限元法的原理

结构内任意形状的单一裂纹如图1所示，有限元网格的所有节点的集合记为S，所有围绕裂纹尖端的单元的节点记为SC，所有被裂纹贯穿的单元的节点(非SC)记为SH，其余节点为常规有限元节点。单元相应分为四类：(1)裂尖单元，单元节点全部由SC组成的单元；(2)贯穿单元，单元节点全部由SH组成的单元；(3)混合单元，单元节点由SC和/或SC与常规有限元节点组成；(4)常规有限元单元。其中，涉及到SC和SC节点的单元需要使用扩充形函数，以下分别介绍各类单元的扩充形函数。

图1 二维裂纹问题中的XFEM扩充节点

由常规有限元形函数、阶跃扩充形函数和渐进位移场扩充形函数，可以将包含二维平面不连续位移场表示为如下形式：

式中，I表示所有节点的集合，J为被贯穿单元的节点集合，K为裂尖单元所有节点的集合；NI，NJ和NK分别代表以上三种节点的形函数；uI代表常规有限元位移自由度，aJ和bK为节点附加自由度，分别代表对贯穿单元和裂尖单元位移场的扩充，成为Heaviside自由度和裂尖自由度；H(x)为阶跃函数，Φα(x)为渐进位移场函数。

2 平面问题裂纹扩展的程序实现

作者以商用数学应用程序Matlab为平台，使用m语言编写了二维问题的XFEM程序。该程序可以实现应力强度因子计算和裂纹扩展模拟的功能。在不引入扩充形函数时，该程序可以退化为常规有限元程序进行求解。程序进行裂纹扩展模拟的运行流程如图2所示，通过断裂韧度和门槛值作为循环结束判断标准的过程，在XFEM程序中进行实现。程序除主函数外，各子函数按功能可以分为初始化、前处理、求解器和后处理四类。在程序网格划分方面，由于XFEM描述裂纹时网格不依赖裂纹边界，而且研究的矩形计算域拓扑结构简单，因此，程序使用了结构化网格进行划分。结构化网格具有网格生成速度快、质量高和数据结构简单的优点。

2.1 算例：斜裂纹矩形板受均匀单向拉伸

为了验证自编程序对I、II复合型裂纹应力强度因子的计算精度，本算例模拟了斜裂纹矩形板受均匀单向拉伸问题。图3(a)所示矩形平板长H=5m，宽W=4m，裂纹长度a=1m，裂纹与载荷方向夹角度θ=67.5°，在上、下边施加均布拉力σ=1Pa。弹性模量E200GPa，泊松比v=0.3。程序网格如图3 (b)所示，约束右上角节点UX自由度，约束右下角节点UX、UY自由度，模拟上下边可转动单轴拉伸边界条件。计算了不同网格密度下2个裂纹尖端的应力强度因子KⅠ、KⅡ，计算结果如表1所示。

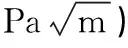
表1 斜裂纹矩形平板(θ=67.5°)单轴拉伸问题计算结果(SIF单位

图2 XFEM程序流程图

由表1可见，网格密度在160×200时计算结果具有较高精度，KⅠ、KⅡ与理论解的相对误差仅为1%左右，程序适合平面复合型问题的求解。将真实变形量放大1e10倍后绘制变形后网格如图 4(a)、(b)所示。

2.2 算例：三点弯曲裂纹扩展

程序对裂纹扩展模拟的有效性通过简支裂纹梁的三点弯曲算例进行验证，如图 5示意。简支梁长L=200mm,高h=40mm，宽度b=2mm，梁跨度中点布置一长a=10mm的初始裂纹。使用平面应力单元离散，网格规模为201×40。图示集中力载荷F=50N。Paris公式系数C=1.5e-11，指数m=3，裂纹扩展判据使用最大周向应力准则。在裂纹扩展计算中，假设断裂韧度KIC无限大，设定裂纹增量Δa=2mm，裂纹从10mm扩展至35mm分为5个裂纹扩展增量步进行计算。

计算结果表明，裂纹开裂角度θc与纯I型三点弯曲的理论值0°差距较小，均在1°左右。裂纹扩展路径如图 6所示，可见程序较好地模拟了纯I型问题的裂纹扩展问题。

图3 斜裂纹矩形板受均匀拉伸

图4 变形后的网格(图示为真实变形放大1e10倍)：

图5 三点弯曲裂纹扩展问题

3 某国产钛合金裂纹扩展性能试验数值模拟

为进一步验证本文扩展有限元程序的有效性与精度，对预研课题[9]某型国产钛合金裂纹扩展性能试验进行了数值模拟。钛合金M(T)试件及试验现场照片如图7所示。

取试验中两件应力比R=0.5试件的结果，对Paris公式进行拟合,如表2所示。

图6 三点弯曲梁的裂纹扩展路径

Paris公式RCnda/dN=C(ΔK)n0.57.516×10-82.906

图7 某国产钛合金M(T)试样及试验现场照片

使用扩展有限元程序对该裂纹扩展过程进行了模拟，目的在于将试验获得的Paris公式参数作为输入，验证程序对裂纹扩展长度的计算精度。有限元的数值模拟中，计算模型尺寸取试验件平均值，宽W=75.12mm，厚B=5.16mm,计算中初始半裂纹长取a=5.28mm，计算载荷加载均布应力σ=103.2MPa，计算网格为340*150。计算循环数与试验数据点对应，计算裂纹长度-循环数曲线如图8所示。

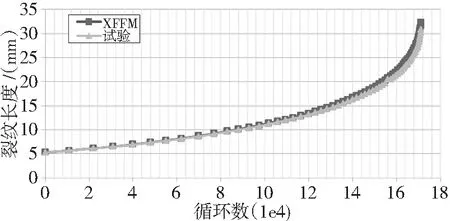
图8 钛合金试件裂纹扩展过程XFEM与

结果表明XFEM与试验裂纹长度最大差异在4%以内。可见扩展有限元程序在模拟裂纹扩展方面具有较好的精度。

4 结语

本文介绍了扩展有限元(XFEM)求解包含不连续位移场断裂力学问题的理论基础，基于Matlab编写了求解二维问题的XFEM程序。该程序可进行平面问题的裂纹扩展模拟。通过算例验证了XFEM方法求解二维问题I型和I、II复合型应力强度因子具有较好的精度；以三点弯曲算例验证了XFEM模拟裂纹扩展路径具有较高精度。通过对某国产钛合金裂纹扩展试验的数值模拟，验证了XFEM程序计算裂纹扩展具有较好的精度。XFEM在模拟裂纹扩展时不需重构网格，该独特优势使其具有较好的工程应用前景。

[1] 穆志韬, 曾本银. 直升机结构疲劳[M]. 北京：国防工业出版社, 2009.

[2] 贾学明, 王启智. 三维断裂分析软件FRANC3D[J]. 计算力学学报, 2004, 21(6): 764-768.

[3] Hou J, Goldstraw M, Maan S, et al. An evaluation of 3D crack growth using ZENCRACK[R]. Defence Science and Technology Organisation Victoria (Australia) Aeronautical and Maritime Research Lab, 2011.

[4] Richard H A, Fulland M, Sch?llmann M, et al. Simulation of fatigue crack growth using ADAPCRACK3D[C]. Fatigue. 2002: 1405-1412.

[5] Belytschko T, Black T. Elastic crack growth in finite elements with minimal remeshing [J]. International Journal for Numerical Methods in Engineering. 1999(86): 1141-1151.

[6] Belytschko T, Gracie R, Ventura G. A review of extended/generalized finite element methods for material modeling[J]. Modelling and Simulation in Materials Science and Engineering, 2009, 17(4): 043001.

[7] sher S, Fedkiw R P. Level Set Methods and Dynamic Implicit Surfaces [M]. Springer, 2003.

[8] 仇仲翼. 应力强度因子手册[M]. 北京: 科学出版社, 1993.

[9] 钛合金XX材料损伤容限性能研究[S]. 直升机设计研究所,2015.

Crack Propagation Numerical Simulation and Implementation by eXtended Finite Element Method

CUI Wei1, XIONG Xin1, YU Jianjian1, WANG Jianjun2

(1.China Helicopter Research and Development Institute, Jingdezhen 333001, China;2.School of Energy and Power Engineering, Beihang University, Beijing 100191, China)

Due to the demands of remeshing tasks, standard Finite element method is confined in crack growth simulations. Based upon research on enriched shape function of discontinues describing, a framework of crack propagation simulation was proposed based upon extended finite element method (XFEM). The theories of crack propagation simulation in XFEM were explained. Then a two-dimensional XFEM implementation within Matlab was presented. The accuracy of XFEM implementation was verified by static fracture mechanics examples and experiment of titanium alloy crack growth test.

eXtended Finite Element Method； crack growth; numerical simulation; Matlab

2016-02-19 作者简介：崔 韦(1985-)，男，天津人，博士，工程师，主要研究方向：直升机结构疲劳与损伤容限。

1673-1220(2016)03-013-05

V215.5+2；TB115.1

A