基于RIPless理论的层析SAR成像航迹分布优化方法

毕辉， 张冰尘， 洪文

1.中国科学院电子学研究所 微波成像技术重点实验室， 北京 100190 2.中国科学院大学， 北京 100190

基于RIPless理论的层析SAR成像航迹分布优化方法

毕辉1,2,*， 张冰尘1， 洪文1

1.中国科学院电子学研究所 微波成像技术重点实验室， 北京 100190 2.中国科学院大学， 北京 100190

层析合成孔径雷达成像(TomoSAR)是通过同一观测区域不同入射角的多幅二维合成孔径雷达(SAR)图像在高程向进行孔径合成，从而实现三维成像。近年来，压缩感知(CS)被用于高程向稀疏场景的重建，高程向重建质量取决于观测矩阵的性质，而航迹分布是影响观测矩阵重构性能的重要因素。相比于度量观测矩阵重构性能的其他约束条件，RIPless理论具有有效、直观和计算简单等优点。提出了一种基于RIPless理论的压缩感知层析SAR成像航迹分布优化准则，从而在航迹数目一定的情况下，获取最优分布以实现高程向优化重建。最后，通过仿真和实验验证了所提优化准则的有效性。

层析合成孔径雷达成像； 压缩感知； RIPless理论； 观测矩阵； 航迹优化

层析合成孔径雷达成像(Synthetic Aperture Radar Tomography, TomoSAR)是一种可以在高程向实现多相位中心分离的三维合成孔径雷达(Synthetic Aperture Radar, SAR)成像技术[1-4]，它通过多幅经过二维SAR处理和配准后的SAR图像(不同的入射角)在高程向上进行孔径合成以获取高程向分辨率，从而实现三维成像。

相比于干涉SAR(Interferometric Synthetic Aperture Radar, InSAR)[5-7]成像，层析SAR成像不仅可以获取散射体的高度信息，同时还能得到散射体高程向分布，实现三维场景的完全恢复。但层析SAR成像所需的观测值(航迹)数目较多，这带来了观测成本增加及时间基线去相关等问题。在航迹数目有限的情况下，针对观测区域高程向分布稀疏的情形，压缩感知(Compressive Sensing, CS)[8-10]方法被用于层析SAR成像[11-13]。根据压缩感知理论，在特定条件下，稀疏信号可以以远低于香农-奈奎斯特采样定理所需的样本数目实现准确重建。压缩感知可有效降低高程向重建所需航迹数且能够实现超分辨[12]，但高分辨率仍需较多航迹数的保证。如何在航迹数目有限的情况下，提高高程向分辨率，将是本文讨论的问题。

压缩感知重建中，观测矩阵需要满足一定的条件。其中，限制等距条件(Restricted Isometry Property, RIP)[10]、零空间性质(Null Space Property, NSP)[10]、限制正交条件(Restricted Orthogonality Property, ROP)[14]，精确重建条件(Exact Reconstruction Criteria, ERC)[15]等对观测矩阵进行评判，但这些评判准则计算复杂，难以在层析SAR成像的优化重建中发挥作用。2011年，Candes和Plan提出了RIPless理论[15]。2014年，Kueng和Gross进一步对该理论进行了完善[16]。RIPless理论认为，在观测矩阵的行向量独立同分布的前提下，若概率分布满足完备性条件和不相干条件，那么就可以以低于香农-奈奎斯特采样定理所需的样本数对稀疏信号进行准确重建。目前RIPless理论已用于分析信号形式对稀疏微波成像[17]性能的影响当中[18]。

在基于压缩感知的层析SAR成像中，观测矩阵与航迹分布密切相关，而航迹分布是影响高程向重建的重要因素。因而如何通过观测矩阵的约束条件对航迹分布进行优化设计，从而实现高程向最优重建将是一个值得研究的问题。本文针对上述问题，结合RIPless理论，提出了一种基于RIPless理论的压缩感知层析SAR成像航迹分布优化准则，在航迹数目一定时获取能对高程向进行优化重建的航迹分布。

本文的结构如下：第1节简要介绍了层析SAR成像模型；第2节介绍了压缩感知重建中的RIPless理论，并将其与层析SAR成像模型相结合，提出了基于RIPless理论的压缩感知层析SAR成像航迹分布优化准则；第3节利用仿真和实验验证了该航迹优化准则的有效性；第4节给出结论。

1 层析SAR成像模型

层析SAR成像中，每条航迹获取的数据均可重建为一幅二维SAR图像，利用多航迹获取的经过误差校正和配准之后的多幅二维SAR图像，可以获取高程向分辨率，实现三维成像。

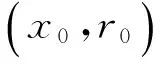
m=1,2,…,M

(1)

将高程向距离s在其范围Δs内离散化为L个均匀分布的点sl(l=1,2,…,L)，则第m个航迹处观测数据为

(2)

式中:rm,l为第m条航迹到高程向第l个点的瞬时斜距。系统的成像模型可以表示为

y=Φγ+n

(3)

(4)

针对高程向分布稀疏的情形，根据上述系统成像模型式(3)，本文利用式(5)对高程向反射函数进行压缩感知重建：

(5)

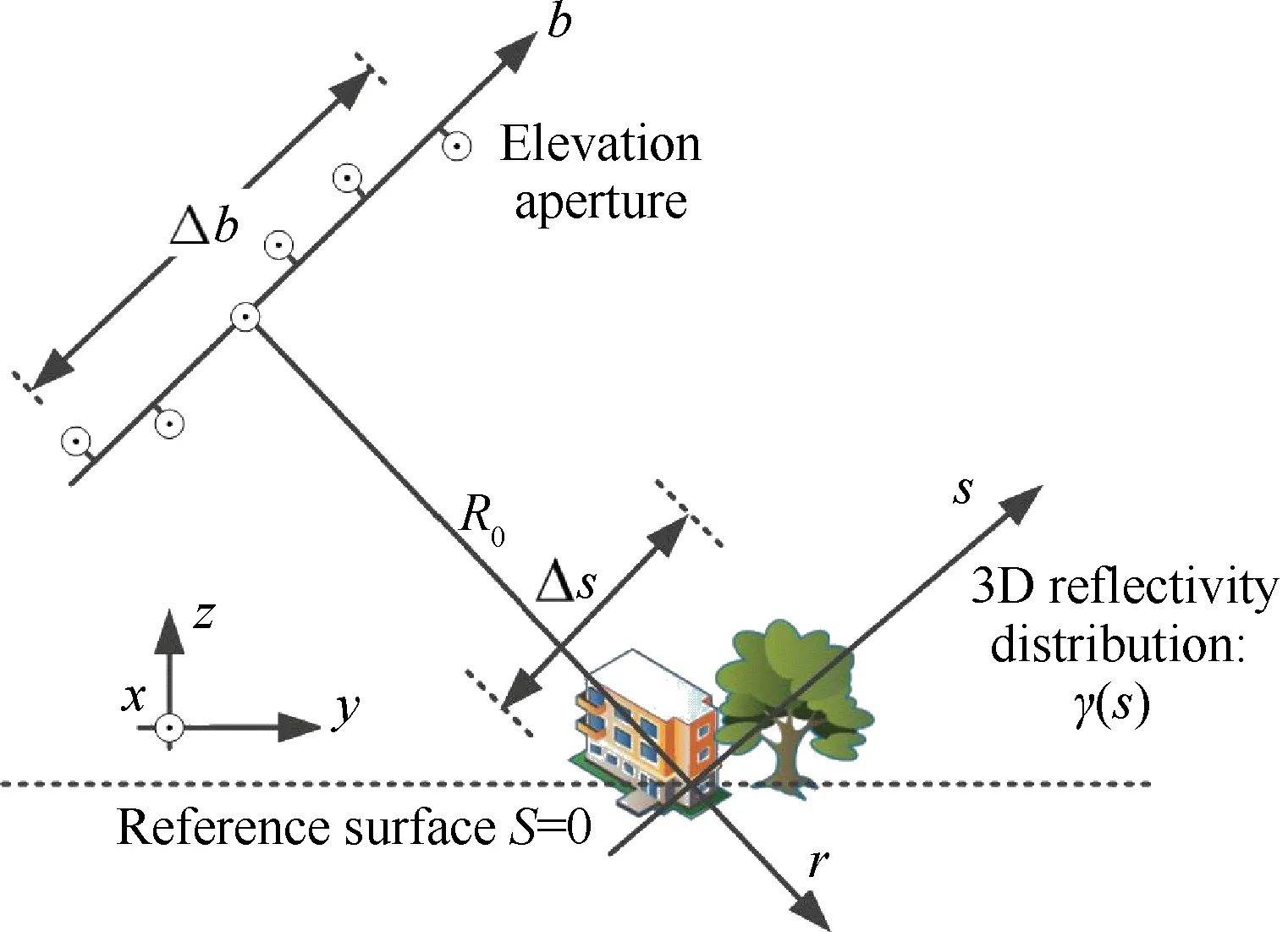
图1 层析SAR成像几何

Fig.1 TomoSAR imaging geometry

2 RIPless理论和航迹优化准则

2.1 RIPless理论

压缩感知观测模型为

z=Ax

(6)

(7)

其中：e1,e2,…,em为m×1的标准基向量。RIPless理论表明，当观测值数目m达到一定的值时，稀疏信号x可以通过式(5)实现准确恢复。而观测值数目仅依赖于概率分布F的两个性质。

完备性 概率分布F需要满足完备性，即协方差矩阵Σ=E[aa*]1/2是可逆的。其中协方差矩阵Σ的条件数为κ，它表示最大奇异值和最小奇异值的比值。

计算不相干参数之前需要对矩阵A进行归一化，使得τmax(E[aa*])=τmin(E[aa*])-1，其中τmax与τmin分别为矩阵E[aa*]的最大和最小特征值。

不相干性 不相干参数μ是满足式(8)的最小值：

(8)

ω≥1时，若观测值数目m满足：

m≥Cω2κμplgn

(9)

式中：C为常数，压缩感知重建的解具有唯一性，并且以1-e-ω的概率等于x。

2.2 航迹优化准则

由2.1节的RIPless理论可以看出，对于特定的观测场景，场景的非零元素的个数p和观测场景的大小n的数值是确定的，当观测值数目一定时，观测场景的重建概率1-e-ω反比于观测矩阵条件数κ与其协方差矩阵不相干参数μ的乘积。

矩阵的条件数是判断矩阵病态与否的一种度量，事实上它表征了矩阵对计算误差的敏感性。条件数越大，表明重建的稳定性就越差，反之重建稳定性越好。

不相干参数μ表征了观测场景点目标在回波中的分散程度，不相干参数越小，分散程度越大，对观测场景进行重建所需观测值数目越少。

依据RIPless理论及上述的分析，本文提出了基于RIPless理论的压缩感知层析SAR成像的航迹优化准则：

航迹数目一定时

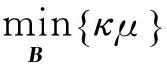
(10)

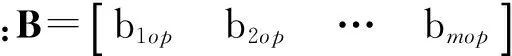
3 仿真、实验结果与分析

本节利用仿真和实验验证所提出的基于RIPless理论的压缩感知层析SAR成像航迹优化准则的有效性。

利用观测场景散射中心估计的准确性和相对均方误差(RelativeMeanSquareError，RMSE)来评价高程向的压缩感知重建效果，其中相对均方误差的定义为

(11)

3.1 仿 真

本节将通过仿真来验证所提出的航迹优化准则。作为对比，将基于本文中所提出的优化准则获取的航迹分布的压缩感知重建结果与优化均匀航迹分布及随机航迹分布的重建结果进行比较，验证航迹优化准则的有效性。需要说明的是，优化均匀航迹分布也是由本文中的优化准则得到的，它表征了所有相邻两条航迹之间的距离相同的航迹分布策略中最优的。

高程场景模拟森林区域的树冠和地面两层分布(两个散射中心)。仿真场景高程向上的地面和树冠两个散射中心分别在20m和50m处，散射强度比为1∶2。仿真参数如表1所示。设定航迹的高程向孔径大小为63m，且在整个实验过程中是保持不变的，即航迹的高程向孔径大小不随航迹数目和航迹分布策略的变化而变化。

表1 仿真参数

图2给出了航迹数目分别为6，7，10时，利用本文所提出的航迹优化准则获得的优化航迹分布对高程向进行压缩感知重建的结果。作为对比，优化均匀航迹分布及随机航迹分布的重建结果也在图2中给出。

由图2中的仿真结果可以看出，首先，当航迹数目为6时，随机航迹分布与优化均匀航迹分布均无法准确重建模拟场景的地面散射中心，而基于RIPless理论的优化航迹可以准确重建地面和树冠两层散射中心的位置。其次，当航迹数目为7和10时，相比于另外两种航迹分布策略，由本文所提出的优化准则获取的航迹分布策略对高程向散射中心的重建更接近于场景真实值。这也说明了基于RIPless理论的层析SAR成像航迹优化准则的有效性。

图3给出了不同的航迹数目下，基于RIPless理论的优化航迹分布、优化均匀航迹分布以及随机航迹分布的重构指标。首先，图3(a)表明，相比于另外两种航迹分布策略，优化航迹分布具有较小的重建RMSE，且随着航迹数目的增多均呈下降趋势。可以看到，当航迹数目超过一定值时，重建RMSE值趋于稳定，这个稳定的值由噪声水平所决定。上述现象出现的原因为航迹数目达到一个值后，继续增加的航迹获取的数据与已有数据的差别越来越小，对高程向重建结果的影响也就逐渐减小。其次，图3(b)表明，航迹数目相同时，基于RIPless理论的优化航迹分布的观测矩阵的不相干参数和其协方差矩阵条件数的乘积均要小于另两种分布策略。由第2节的分析可知，航迹数目一定时，不相干参数和条件数的乘积越小，重建的稳定性越好，重建效果越好。这也很好地验证了图2中的重建结果和结论。另外需要说明的是，基于RIPless理论的最优航迹分布策略对应的观测矩阵的不相干参数随着航迹数目的增多呈现下降趋势，但其协方差矩阵的条件数的变化不规则，这是因为航迹数目越多，观测场景的点目标分布越分散，进行降采样时丢失的信息就越少，则重建结果越好。而观测矩阵的协方差矩阵的条件数表征了矩阵的病态程度，它只表示最大和最小特征值的比值，而和矩阵的行数没有必然的联系。本文中的条件数只是保证在特定航迹数目时，观测矩阵的条件数与其协方差矩阵的不相干参数的乘积取得最小值。

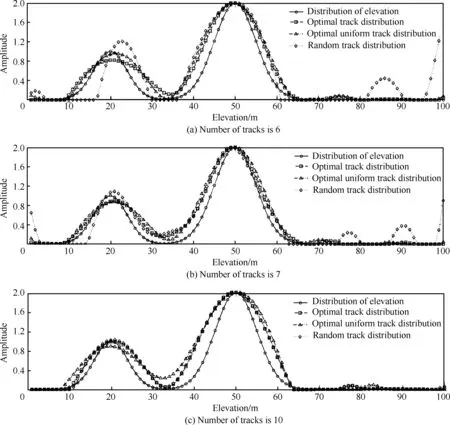
图2 不同航迹分布高程向重建结果

Fig.2 Reconstructed results of elevation with different track distributions

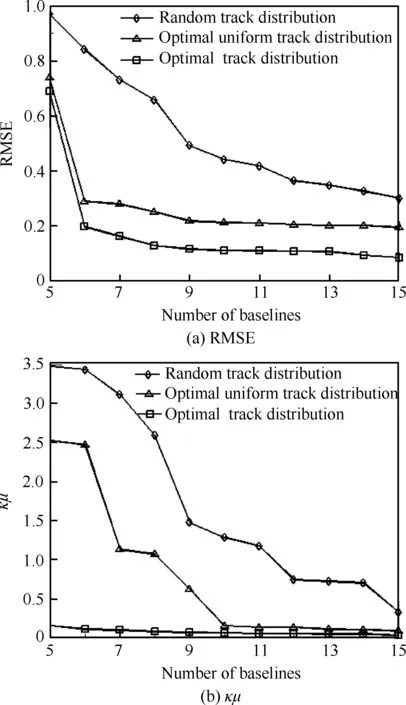
图3 不同航迹分布对高程向进行重建的指标比较

Fig.3 Comparison of reconstructed parameters along elevation with different track distributions

3.2 实 验

为了进一步说明所提出的基于RIPless理论的层析SAR成像航迹优化准则有效性，本节利用德国宇航局的E-SAR传感器[19]于2007年获得的P波段10条航迹的BioSAR数据(瑞典南部区域)进行实验验证[20]。实验参数如表2所示。

表2 实验参数

实验森林区域如图4(a)所示，实验中选取一个距离切片(见图4(b))，对该距离向切片上的每个方位-距离分辨单元依次进行高程向压缩感知重建。首先利用所有10条航迹(其分布如图5所示)数据进行重建，然后从所有航迹中取其中的7条航迹数据进行重建。本节将基于RIPless理论的优化航迹分布的重建结果与优化均匀航迹分布及随机航迹分布的结果相比较，以验证该优化准则。

图6(a)给出了全部10条航迹数据对高程向进行压缩感知重建的结果，图6(b)为航迹数目为7时，优化航迹分布的高程向重建结果，图6(c)和图6(d)则给出了从10条航迹中随机选取7条航迹后的高程向重建结果。由图6的结果可知，7条航迹下的优化航迹分布的高程向重建结果接近于10条航迹的结果，可以准确重建地面和树冠两层区域，而图6(c)和图6(d)中的重建结果中均出现了无法区分地面和树冠两层散射中心的现象(如图中矩形框内的区域所示)。图6(b)、图6(c)和图6(d)中不同航迹分布策略的观测矩阵的不相干参数与其协方差矩阵的条件数的乘积值的大小也准确反映了高程向的重建结果，观测矩阵的不相干参数与其协方差矩阵的条件数的乘积值越小，高程向重建效果越好。

图4 实验场景

Fig.4 Experimental scene

图5 航迹分布

Fig.5 Track distribution

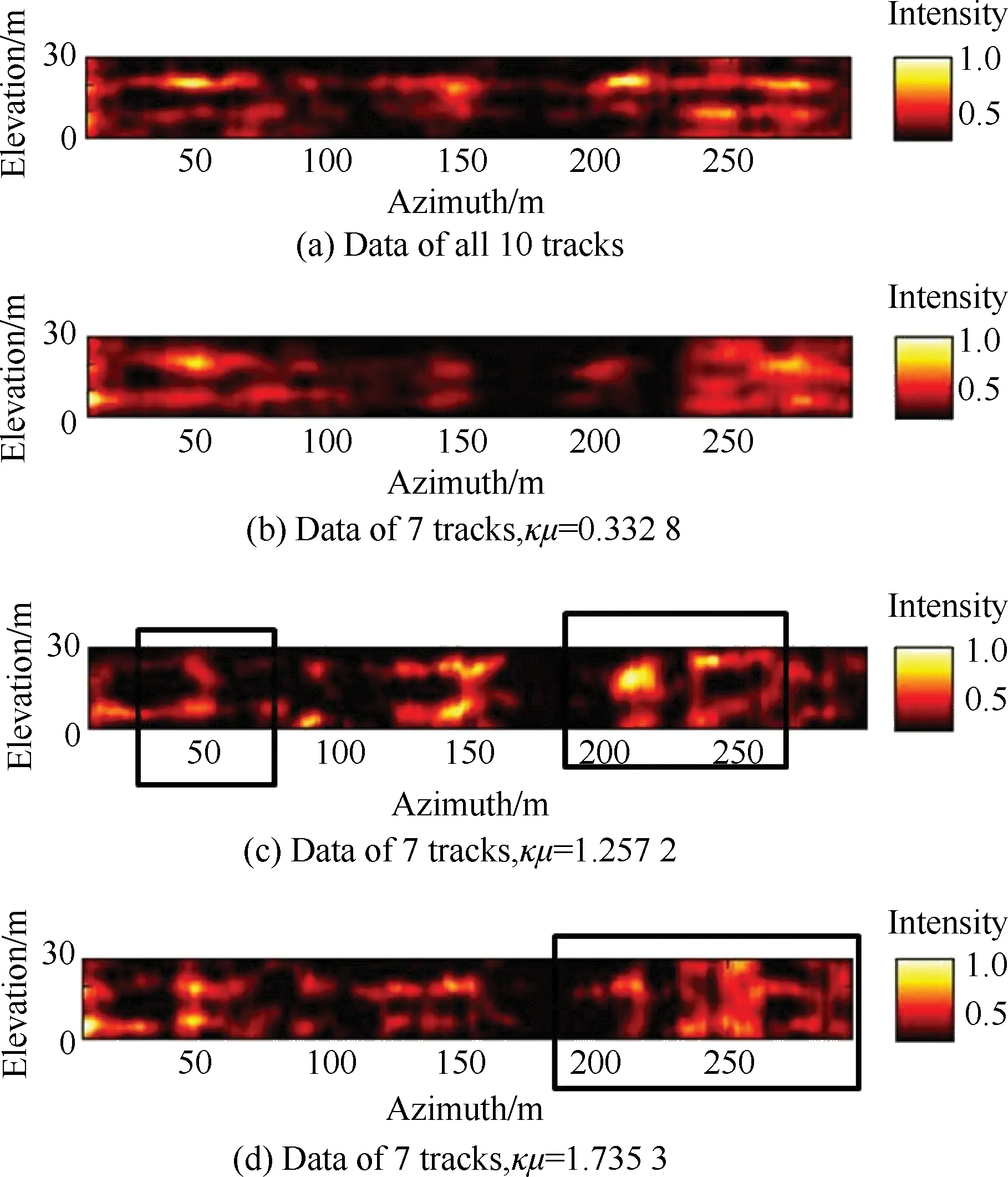
图6 不同航迹分布策略下的森林区域压缩感知重建结果

Fig.6 CS reconstructed results along elevation for forest with different track distributions

4 结 论

本文研究了航迹分布对压缩感知层析SAR成像高程向重建性能的影响。

1) 针对层析SAR成像，提出了一种基于RIPless理论的压缩感知层析SAR成像航迹优化准则。

2) 利用所提出的优化准则获取的航迹分布对高程向进行压缩感知最优重建。

3) 所提出的准则计算简单，能在观测几何确定的情况下，快速给出航迹分布策略。

另外还需说明的是，观测矩阵的不相干参数随着航迹数目的增加而减少，而表征观测矩阵对应的协方差矩阵的病态性的条件数的变化则是没有规律的。基于RIPless理论的航迹优化准则只是保证在航迹数目确定时，获取的航迹分布策略对应的条件数与其协方差矩阵的不相干参数的乘积是最小的，且该乘积的值随着航迹数目的增加而逐渐减小。

致 谢

感谢中国林业科学研究院资源信息研究所陈尔学教授提供的Biomass数据集(龙计划项目第三期支持，ID10609)，帮助我们验证了算法的实用性。

[1] REIGBER A, MOREIRA A. First demonstration of airborne SAR tomography using multibaseline L- band data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(5): 2142-2152.

[2] FORNARO G, LOMBARDINI F, SERAFINO F. Three-dimensional focusing multipass data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(3): 507-517.

[3] FORNARO G, LOMBARDINI F, SERAFINO F. Three-dimensional multipass SAR focusing: Experiments with long-term spaceborne data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(4): 702-714.

[4] LOMBARDINI F, MONTANARI M, GINI F. Reflecitivity estimation for multibaseline interferometric radar imaging of layover extended sources[J]. IEEE Transactions on Signal Processing, 2003, 51(6): 1508-1519.

[5] BAMLER R, HARTL P. Synthetic aperture radar interferoetry [J]. Inverse Problem, 1998, 14(4): 1-54.

[6] GABRIEL A, GOLDSTEIN R. Crossed orbit interferometry: Theory and experimental results from SIR-B[J]. International Journal of Remote Sensing, 1988, 9(5): 857-872.

[7] 胡庆东, 毛士艺. 干涉合成孔径雷达基线的估计[J]. 航空学报, 1998, 19(S1): 20-24. HU Q D, MAO S Y. Estimation of interferometric SAR baseline[J]. Acta Aeronoutica et Astronautica Sinica, 1998, 19(S1): 20-24 (in Chinese).

[8] DONOHO D. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.

[9] CANDES E J, TAO T. Near-optimal signal recovery from random projections: Universal encoding strategies[J]. IEEE Transactions on Information Theory, 2006, 52(12): 5406-5425.

[10] CANDES E, ROMBERG J, TAO T. Stable signal recovery from incomplete and inaccurate measurements[J]. Communications on Pure and Applied Mathematics, 2006, 59(8): 1207-1223.

[11] BUDILLON A, EVANGELISTA A, SCHIRINZI G. SAR tomography from sparse samples[C]//International Geoscience and Remote Sensing Symposium, 2009: 865-868.

[12] ZHU X, BAMLER R. Very high resolution spaceborne SAR tomography in urban environment[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(12): 4296-4308.

[13] ZHU X, BAMLER R. Tomographic SAR inversion L1-norm regularization-the compressive sensing approach[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(10): 3939-3846.

[14] CANDES E, TAO T. Decoding by linear programming[J]. IEEE Transactions on Information Theory, 2005, 51(12): 4203-4215.

[15] CANDES E, PLAN Y. A probabilistic and RIPless theory of compressed sensing[J]. IEEE Transactions on Information Theory, 2011, 57(11): 7235-7254.

[16] KUENG R, GROSS D. RIPless compressed sensing from anisotropic measurements[J]. Linear Algebra and its Applications, 2014, 441: 110-123.

[17] ZHANG B C, HONG W, WU Y R. Sparse microwave imaging: principles and applications[J]. Science China Information Sciences, 2012, 55(8): 1722-1754.

[18] 赵曜, 张冰尘, 洪文， 等. 基于RIPless理论的稀疏微波成像波形分析方法[J]. 雷达学报, 2013, 2(3): 265-270. ZHAO Y, ZHANG B C, HONG W, et al. RIPless based radar waveform analysis in sparse microwave imaging[J]. Journal of Radars, 2013, 2(3): 265-270 (in Chinese).

[19] HORN R. The DLR airborne SAR project E-SAR[C] //International Geoscience and Remote Sensing Symposium, 1996: 1624-1628.

[20] HAJNSEK, I, SCHEIBER R, ULANDER L, et al. BioSAR 2007: Technical assistance for the development of airborne SAR and geophysical measurements during the BioSAR 2007 experiment[R]. Oberpfaffenhofen: DLR, 2008.

毕辉 男， 博士研究生。主要研究方向： 稀疏微波成像、 层析合成孔径雷达成像。

Tel: 010-58887130

E-mail: bihui1991@163.com

张冰尘 男， 博士， 研究员， 硕士生导师。主要研究方向： 雷达系统与雷达信号处理、新体制雷达。

Tel: 010-58887124

E-mail: bczhang@mail.ie.ac.cn

洪文 女， 博士， 研究员， 博士生导师。主要研究方向： 三维微波成像等新概念、 新方法。

Tel: 010-58887105

E-mail: whong@mail.ie.ac.cn

Received： 2015-01-21； Revised： 2015-05-04； Accepted： 2015-05-10； Published online： 2015-05-25 09:55

URL： www.cnki.net/kcms/detail/11.1929.V.20150525.0955.004.html

Foundation item： CAS/SAFEA International Partnership Program for Creative Research Team

*Corresponding author. Tel.： 010-58887130 E-mail: bihui1991@163.com

Track distribution optimization method based on TomoSAR viaRIPless theory

BI Hui1,2, *, ZHANG Bingchen1, HONG Wen1

1.ScienceandTechnologyonMicrowaveImagingLaboratory,InstituteofElectronics,ChineseAcademyofSciences,Beijing100190,China2.UniversityofChineseAcademyofSciences,Beijing100190,China

Synthetic aperture radar tomography (TomoSAR) applies measured repeat-pass SAR images to synthetize an aperture in the elevation direction, so as to achieve three-dimensional imaging. In recent years, compressive sensing (CS) has been used for elevation reconstruction for the sparse elevation distribution. The imaging quality of elevation of CS-based TomoSAR depends on the recovery property of measurement matrix, which is affected by the track distribution. Compared to other restrictions of recovery property for measurement matrix, RIPless theory is intuitionistic, effective and simple to calculate. In this paper, we propose a track distribution optimal criterion for CS-based TomoSAR via RIPless theory to optimize the distribution of flight tracks and achieve optimal reconstruction of elevation when the number of tracks is fixed. Simulation and experimental results validate the validity of the proposed optimization criterion.

synthetic aperture radar tomography; compressive sensing; RIPless theory; measurement matrix; track optimization

2015-01-21；退修日期：2015-05-04；录用日期：2015-05-10； < class="emphasis_bold">网络出版时间：

时间： 2015-05-25 09:55

www.cnki.net/kcms/detail/11.1929.V.20150525.0955.004.html

中国科学院创新团队国际合作伙伴计划

.Tel.： 010-58887130 E-mail: bihui1991@163.com

毕辉， 张冰尘， 洪文． 基于RIPless理论的层析SAR成像航迹分布优化方法[J]． 航空学报, 2016, 37(2): 680-687. BI H, ZHANG B C, HONG W. Track distribution optimization method based on TomoSAR via RIPless theory[J].Acta Aeronautica et Astronautica Sinica, 2016, 37(2): 680-687.

http://hkxb.buaa.edu.cn hkxb@buaa.edu.cn

10.7527/S1000-6893.2015.0131

V243.2; TN958

： A

： 1000-6893(2016)02-0680-08

*