M-型皱褶芯材夹层板吸能性能研究

周华志， 王志瑾南京航空航天大学 航空宇航学院， 南京 210016

M-型皱褶芯材夹层板吸能性能研究

周华志， 王志瑾*
南京航空航天大学 航空宇航学院， 南京 210016

作为先进复合材料夹层结构，皱褶夹层板是一种具有众多优点的新型夹层板结构。本文建立了带有缺陷的皱褶芯材有限元模型，对M-型皱褶芯材的能量吸收率和几何参数之间的关系进行了研究。压缩试验仿真结果与CELPACT项目中的试验结果相符。与蜂窝芯材相比，皱褶芯材在吸能性能上表现出了很大的优势，其能量吸收率是蜂窝芯材的两倍多。此外，本文采用响应面法获得了M-型皱褶芯材几何参数和吸能性能指标之间的关系。最后，以吸能性能最优为目标，采用拉丁超立方抽样(LHS)方法获得初始样本，以多目标非支配排序遗传算法(NSGA-II)对皱褶芯材进行了优化。

皱褶夹层板； 抗坠撞； 能量吸收率； 响应面； 优化

提高直升机的抗坠毁能力，是现代直升机，特别是武装直升机生存能力设计的主要要求之一。直升机抗坠毁设计过程中，机身设计非常关键。而机身设计中，机身下腹部所处的位置决定了它在坠撞时最有可能(不考虑起落架)先接触到地面，因而其吸能能力的设计就成为了机身结构抗坠性设计的重中之重。

机身下腹部结构吸能主要是通过结构的大塑性变形和破碎来完成的。为了尽可能地减轻重量，直升机必须使用能量吸收率(Energy Absorption Coefficient, EAC)高的材料。材料的能量吸收率是指单位质量的抗坠毁吸能材料在飞行器触地坠毁时通过材料本身的变形、压溃过程吸收的机身冲击能量的多少。为了获得高EAC的结构和材料，国内外作了很多的研究。荷兰的国家航空实验室(NLR)设计的波纹梁结构是一种有效的缓冲吸能结构，已经成功地在NH-90直升机的地板下结构中用做缓冲吸能元件[1]。刘瑞同等研究了波纹梁的缓冲吸能原理，并讨论了结构尺寸的不同对波纹梁在轴向准静态载荷下的吸能能力和峰值载荷的影响[2]。龚俊杰和王鑫伟对长单波纹梁、短单波纹梁和三波纹梁的吸能能力进行了数值模拟[3]。Zhou等发现中等冲击速度下石墨/环氧复合材料单波纹板准静态加载和动态加载的抗坠毁性能无明显差异；此外，不同波纹圆心角的单波纹板的失效模式不同；他们还提出了一种刚度修正模型来预测单波纹板的失效模式[4]。

除波纹梁外，薄壁管是另一种有效的缓冲吸能结构。Indermuehle等对复合材料方锥管的碰撞冲击进行了仿真[5]。Nagel和Thambiratnam通过准静态分析研究了锥形薄壁管的壁厚、锥角、锥面数以及横截面尺寸对吸能能力的影响，获得了一些对抗坠毁设计有指导意义的结论[6]。Santosa等发现，泡沫填充材料的存在改变了薄壁管的破坏模式，从而更多的能量会在变形中耗散掉[7]。

复合材料结构因其特殊的损伤与破坏机理而具有更好的缓冲吸能性能。Tan和Chen研究了新型编织复合材料多胞结构(TCCSs)的吸能能力，发现：胞元越小，结构的吸能能力越好；胞元开角越接近90°，其吸能能力越好[8]。

倪先平等对波纹梁、厚蜂窝和T型组合件等元件进行了吸能特性研究，发现厚蜂窝下底板盒段和波纹梁盒段都有很好的吸能特性[9]。

皱褶芯材结构具有夹芯板结构共有的高比强度、高比刚度、消声和隔热等特性，芯材结构形式的多样性决定了皱褶夹芯板具有非常优异的结构可设计性，可以制造出如变厚度板、阶梯板和曲面板等各种各样的结构形式，而这是蜂窝夹芯结构做不到的。

皱褶夹芯板具有大量的空腔，为大塑性变形提供了可能性。因而，这种结构可能具有很强的吸能能力。

关于皱褶芯材的性能，国内外也做了很多的研究工作。王志瑾和Khaliulin对皱褶芯材结构的几何设计方法进行了研究[10]。曾会华和徐庆华给出了双阶型芯材和圆筒型芯材的构造方法[11]。张慧和王志瑾采用理论解析与数值分析两种方法，对V型皱褶芯材的剪切弹性模量进行了研究[12]。Heimbs等开发出了一套用于压剪组合试验的测试设备，并进行了一系列的试验；在对皱褶芯材的非线性力学性能的数值仿真研究中他们发现，网格密度对计算结果的精确度有一定的影响，而模型尺寸对计算结果的影响非常小；他们还建立了一套夹层板性能仿真的方法，并用此方法获得了皱褶芯材各方向压缩和剪切载荷下的应力-应变曲线；此外，他们还对材料破坏后的应力-应变曲线和材料的吸能性能进行了讨论[13-15]。

Baranger等开发出了一套考虑了皱褶芯材缺陷的建模方法。用该方法建立的模型进行的仿真计算结果与试验结果符合得很好[16]。

从上面的介绍可以看出，对皱褶夹芯板，国内外虽然已经有了一定的研究，但是主要偏向于结构的刚度和强度仿真，也就是说，对皱褶芯材和皱褶夹芯板的抗坠毁吸能性能的研究，不管是面内冲击还是面外冲击，研究的都很少。既然皱褶芯材具有抗坠毁结构所共有的一系列特点，对其进行抗坠毁吸能性能的研究是很有必要的。

本文采用有限元分析方法，对M-型皱褶芯材各参数对其吸能能力的影响进行了分析和讨论，采用响应面法求解能量吸收率和几何参数之间的关系。据此，以吸能性能最优为目标对皱褶芯材进行了优化。

1 皱褶芯材压缩吸能及优化设计理论

1.1 数值求解方法

皱褶芯材的压缩吸能过程可以看做一个高度非线性的准静态问题，并具有相当复杂的内部接触和后屈曲问题。对于这样的问题，显式动力学有限元分析方法是一种有效的解决方法。该方法适用于求解动力学响应时间相对较短的大型模型以及进行典型非线性事件或过程的分析，使用连续的大变形理论(模型可以经历大的变形和扭转)或几何线性变形理论(应变和位移较小)，可以进行非线性耗散产生热量的绝热应力分析和复杂接触的准静态分析。

ABAQUS/Explicit是一种典型的显式动力学有限元分析求解器。它采用中心差分方法对运动方程进行显式的时间积分，应用上一个增量步的动力学状态计算下一个增量步的动力学状态。该方法占用的资源随模型尺寸线性增长，计算效率高。因此，本文采用ABAQUS/Explicit对M-型皱褶芯材Z方向准静态压缩问题进行求解。

动力学基本方程为

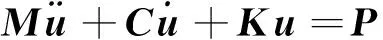
(1)

采用中央差分积分法则对式(1)进行求解。中央差分积分法则可以表述为

(2)

式中：i为显式动力学分析步中的增量数；Δt为显式动力学分析步中的时间增量。

上述的显式积分法则很简单，但其自身并不能保证显式动力学程序的高计算效率。高计算效率的关键在于使用了对角单元质量矩阵，这是由于在积分开始时，根据牛顿第二定律有

(3)

式中：P(i)为第i个增量步中的载荷向量；I(i)为第i个增量步中的内力向量。此处使用了集中质量矩阵，因为其逆矩阵易于计算，且质量矩阵的逆矩阵与内力向量相乘时只需要n次计算，n为模型的自由度。

显式有限元分析的积分是通过许多小的时间增量来完成的。而中心差分方法可能会发散。在无阻尼的情况下，保证计算不发散的时间增量Δt需满足

(4)

式中：ωmax为系统中的最高频率。

有阻尼的情况下，Δt需满足

(5)

式中：ξ为最高频率模态的临界阻尼部分。

1.2 优化设计理论

皱褶芯材的吸能能力和芯材多个几何参数相关。直接进行多参数优化分析，计算耗时长、效率低。为此，本文首先利用拉丁超立方抽样(LHS)方法在设计变量空间中选取一定的样本点，分别建立有限元模型，获得各样本点的吸能性能响应，利用这些样本点和响应值建立吸能性能的响应面模型。最后采用多目标非支配排序遗传算法(NSGA-II)对响应面模型进行优化。

1.2.1LHS抽样

LHS抽样最早由Mckay提出，由Stein给出比较数学化的表述[17]。LHS是一种可以替代MonteCarlo方法的效果好的方差缩减技术，在仿真模拟、优化计算和可靠性计算方面得到较为广泛的应用。其抽样步骤为：①将每一维分成互不重叠的M个区间，每个区间有相同的概率；②在每一维里的每一个区间中随机抽取一个点；③再从每一维里随机抽取出第②步中选出的点并组成样本点。

1.2.2 多项式响应面模型

多项式响应面是多学科设计优化中最为常用的一种代理模型[18]，其基本数学表达形式为

(6)

式中：xi和xj分别为m维自变量x的第i和j个分量；β0、βi和βij为未知参数，将它们按照一定次序排列，构成列向量β。求解多项式拟合模型的关键就是求解列向量β。

1.2.3NSGA-II

NSGA-II全称为“带有精英策略的非支配排序遗传算法”[19]，该算法主要考虑种群个体之间的支配和非支配关系，以此达到快速非支配排序的目的。其算法流程如图1所示。

图1 NSGA-II流程图

Fig.1 Flowchart of NSGA-II

2 M-型皱褶芯材结构及其有限元建模

2.1 M-型皱褶芯材的几何构成

图2 M-型皱褶芯材几何参数

Fig.2 Geometric characteristics of M-type folded core

等高度的M-型皱褶芯材是由矩形单元1和平行四边形单元2构成[10]，单元之间沿边沿相连。从构造上可以分出M形的凹线3、凸线4和锯齿形线5。M-型皱褶芯材的几何参数如图2所示。图2中：2S为M形线的步长；2L为锯齿形线的步长；V为M形线的折幅；B为锯齿形线的间距；H为芯材高度。

为了更方便地进行皱褶芯材参数的变化和建模，给出如式(7)所示的导出参数。

(7)

这些参数和锯齿形线的间距B之间是完全独立的，在芯材高度H给定的前提下，这些参数的组合可以完全确定一种M-型皱褶芯材构型。

2.2 有限元建模

本文采用Python语言结合ABAQUS有限元分析软件进行有限元的参数化建模。模型的规模对皱褶芯材的性能没有太大的影响。为了简化模型，降低计算成本，选择的模型规模为横排3个胞元，纵排6个胞元。

网格尺寸对模型的计算精度有一定的影响。网格过粗，会导致计算精度差，计算出来的结果没有意义；网格过细，计算成本太高，且网格细到一定程度会导致网格长厚比太小，无法继续使用壳单元建模。考虑到建模方便以及计算精度，最终选定网格尺寸为1mm。而网格的类型选为四边形减缩积分壳单元S4R。

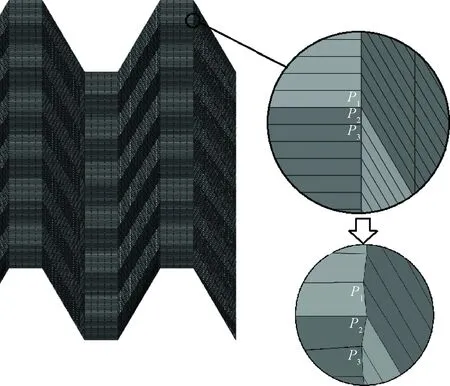
图3 节点偏移法

Fig.3 Node shaking method

由于制造工艺等原因，实际皱褶芯材必然会存在一定的缺陷，从而导致芯材的强度和刚度等的下降。在仿真计算中，对这些缺陷的处理有3种方法：材料性能折减法、节点偏移法和由Baranger等提出的缺陷模拟方法[16]。本文选择的是节点偏移法。该方法如图3所示，通过随机改变每一个节点的位置来模拟皱褶芯材的缺陷，可以较好地模拟皱褶芯材成形过程中的偏移和损伤，但无法处理材料的缺陷。在偏移的过程中，偏移向量采用球坐标表示：方位角和仰角在0°～360°之间随机选取；偏移距离在0～0.5mm之间随机选取。偏移距离上限定为0.5mm是因为网格尺寸为1mm，更大的偏移距离可能会导致网格扭曲，有限元计算无法进行。

芯材上下各加一个刚性面板，下面板与芯材接触，上面板离芯材有一段很短的距离，以避免随机改变的节点位置高于上面板。上下面板与芯材之间通过接触约束连接，接触算法采用罚函数法，摩擦系数取为无穷大，以模拟真实结构中面板和芯材的胶接结构。计算中涉及到芯材的后屈曲大变形阶段，因此定义了芯材的自接触。

边界条件为下面板固支，上面板具有一个向下的恒定速度，以模拟面板与芯材接触并压缩芯材的过程。最终的有限元模型如图4所示。

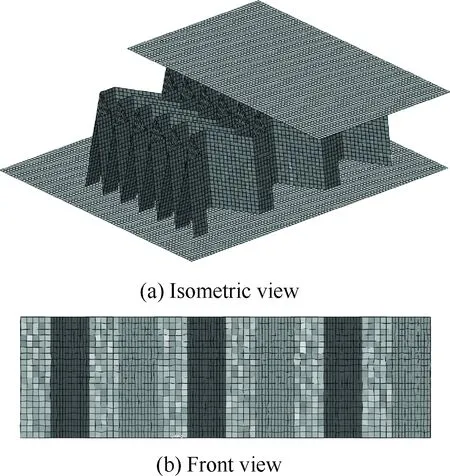
图4 皱褶芯材有限元模型

Fig.4 Finite element model of folded core

2.3 材料性能

皱褶芯材所用材料为芳纶纸。由于该材料的压缩应力-应变曲线比较复杂，因此在建立有限元模型时，对其进行了一定程度的简化，将其简化为理想弹塑性曲线。简化后的应力-应变曲线和原应力-应变曲线如图5所示。图中的原始应力-应变曲线来自文献[20]。由于皱褶芯材受压时材料很快发生屈曲，弹性变形阶段吸收的能量相较于吸收的总能量而言很少，故将弹性段性能进行如此的简化是可行的。之后的有限元计算结果与试验结果的对比也说明了这一点。

图5 材料应力-应变曲线

Fig.5 Stress-strain curves of material

在ABAQUS中，分别使用Elastic模块及Plastic模块定义材料的弹塑性行为，将材料定义为理想弹塑性材料。

2.4 仿真结果

为了验证模型的正确性，取文献[13]中的试件参数建立有限元模型，将仿真得到的等效压缩应力-应变曲线和文献[13]中试验测得的等效应力-应变曲线进行了比较。等效应力-应变曲线如图6所示，其中：等效应力定义为压力与皱褶芯材在垂直于压力的平面上的投影面积之比；等效应变定义为芯材压缩长度与皱褶芯材高度之比。

可以看出，用本文模型仿真得到的曲线和试验得到的曲线在大部分区域都是吻合的，但仿真所得的屈服应力略低于试验值。这是由于在材料的简化模型中，舍去了真实材料中存在的峰值应力段，但屈服应力的误差不大，且影响很小，可以接受。此外，后屈曲段计算结果相较于试验结果也偏低，这是由于在芯材的自接触中忽略了摩擦。压缩过程中，皱褶芯材吸收的能量与其应变的关系曲线如图7所示。可以看出，二者相差较小。

图6 等效应力-应变曲线

Fig.6 Equivalent stress-strain curves

图7 能量-等效应变曲线

Fig.7 Energy-equivalent strain curves

图6中的曲线可以分为4段：弹性段、屈曲段、平直段和致密段。在弹性段，等效应力和应变等比例上升，芯材材料处于弹性变形过程，该过程中可能伴随部分皱褶芯材壁板屈曲；当足够多壁板都发生屈曲时，皱褶芯材发生屈曲，等效应力下降；应变继续增加，应力-应变曲线进入平直段，芯材持续屈曲及压溃，这个过程中等效应力保持不变；当变形足够大时，芯材进入致密段，其各个壁板互相接触，芯材被压实，等效应力开始迅速增加。在致密段，可以认为皱褶芯材已经不具备减震缓冲能力。

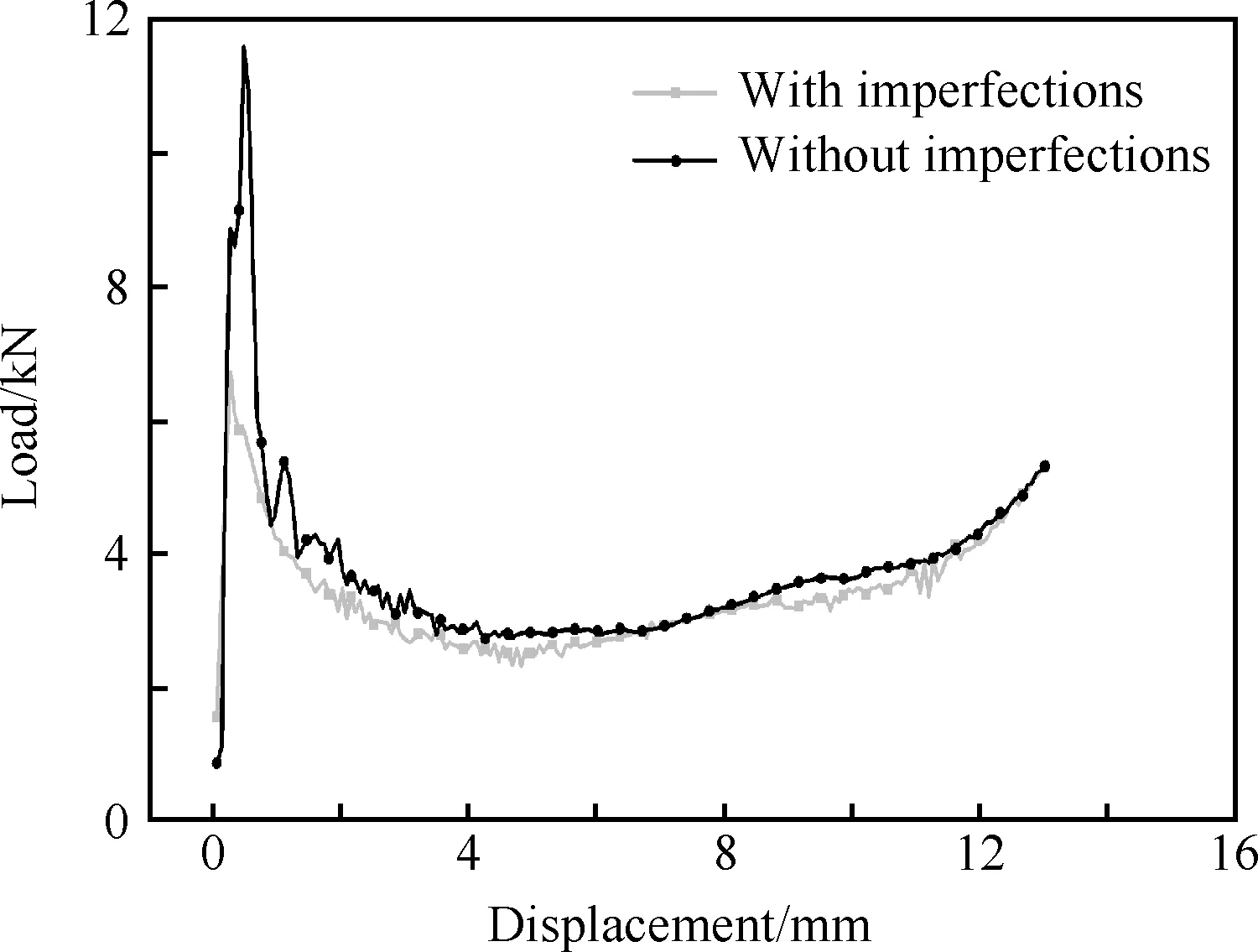
图8 有缺陷和没有缺陷的皱褶芯材载荷-位移曲线

Fig.8 Comparison of load-displacement curves of folded core with and without imperfections

有缺陷芯材和没有缺陷芯材的载荷-位移曲线的对比如图8所示。从8图中可以看出，缺陷导致芯材屈服应力下降了很多。

加载速度对皱褶芯材吸能能力的影响如图9所示。从图中9可以看出，在选取的变化范围内，加载速率对吸能性能几乎没有影响。考虑到试验中加载速度v为2mm/s，本文中加载速度也取为2mm/s。

图9 不同加载速度下的吸能-位移曲线

Fig.9 Energy absorbed-displacement curves at different compression speeds

2.5 吸能性能对比

为了验证皱褶芯材具有强的吸能能力，本文将皱褶芯材与铝蜂窝芯材的吸能进行了对比。根据文献[21]中的蜂窝芯材参数，本文设计了A=13.5mm，B=5.9mm，λ=30°，α=9°，H=25mm的皱褶芯材，其密度比约为0.1，密度比和芯材高度与文献[21]中的蜂窝芯材保持一致。材料参数与文献[21]中的参数一致。压缩过程中皱褶芯材的变形过程如图10所示。压缩9mm后，经有限元仿真计算获得皱褶芯材压缩过程中吸收的能量，压溃质量取为整个皱褶芯材的质量，代入式(8)计算。

EAC=吸收的能量/吸能结构质量

(8)

计算得到的皱褶芯材EAC=9.93kJ/kg。而文献[21]中蜂窝芯材压缩9mm后的EAC=4.01kJ/kg。皱褶芯材的吸能效率可达蜂窝芯材的两倍多，说明皱褶芯材具有优越的吸能性能，可以作为抗坠毁压缩吸能材料使用。

图10 皱褶芯材压缩过程

Fig.10 Compression process of folded core

3 皱褶芯材的优化设计

为获得具有最佳吸能效率的皱褶芯材几何构型，需对皱褶芯材几何参数进行优化。

3.1 优化问题的数学描述

M-型皱褶芯材具有5个几何参数。其中高度H一般是给定的，本文给定高度H=20mm，与文献[13]中皱褶芯材试件的高度一致。采用LHS方法取得若干组参数，计算其EAC。以此为基础构建响应面函数。在获得响应面函数的基础上，采用NSGA-II进行优化。

皱褶芯材的设计过程中需要考虑工艺的影响，有些参数的组合是不可能制造出来的，为此，需要对参数进行适当的约束。

优化问题的数学描述如式(9)所示。

(9)

式中：t为材料厚度，这个参数一般都是指定的，本文中取0.3mm；第2个公式为工艺约束，它表示皱褶芯材V形线的跨距不能过小，以便于加工成形。

3.2 EAC的响应面函数

优化时若对每组样本点分别建模进行计算以获得能量吸收率，耗时长，效率低。一种提高效率的方法是求解能量吸收率的响应面函数，以此替代建模求解的过程。为了获得EAC的响应面函数，采用LHS方法在一定范围内随机选择了30组样本点，对这30个样本点分别计算EAC，获得的EAC的响应面函数为

EAC=664.76B-608.38A-3 270.23λ-

36 369α-61.84B2+8.55BA-

85.50Bλ-58.34Bα+7.30A2+

141.87Aλ+543.88Aα-2 064.32λ2+

440.98λα+47 860.32α2+15 377.53

(10)

式中：所有角度的单位为弧度。

为了确定拟合结果的正确性，另外随机取了98组样本点，按式(11)计算EAC的误差值。

(11)

式中：ε为误差；EACs为有限元仿真得到的吸能系数；EACc为采用代理模型计算得到的吸能系数。通过对各误差值进行算术平均，得到其平均误差为3.24%，拟合结果能够真实反映EAC随几何参数的变化。

3.3 优化结果

采用LHS方法获得初始样本点，采用NSGA-II对皱褶芯材进行优化，优化过程中采用响应面函数计算设计点的EAC。

图11 优化历史

Fig.11 Optimization history

优化历史如图11所示。图中：矩形代表符合约束条件的设计点；菱形代表不符合约束条件的设计点。可以看出，优化结果收敛得很好。优化结果为：A=4.5mm，B=5.3mm，α=7.3°，λ=33.2°，EAC=8.748kJ/kg。

4 总 结

1) 建立了带有缺陷的皱褶芯材准静态压缩吸能有限元模型，模型分析结果与试验相符。皱褶芯材中缺陷的存在会降低皱褶芯材等效屈服应力，从而降低结构的承载能力，但对吸能能力影响不大。

2) 将皱褶芯材吸能能力和蜂窝芯材作了对比，皱褶芯材能量吸收率可达蜂窝芯材的两倍多，说明皱褶芯材具有更好的吸能性能。

3) 给出了EAC随几何参数变化的响应面函数。

4) 对皱褶芯材进行了优化设计，得出了满足约束条件下吸能性能最优的皱褶芯材几何参数。

[1] LAVOIE J A, MORTON J. Design and application of a quasistatic crush test fixture for investigating scale effects in energy absorbing composite plates: NASA Contractor Report 4526[R]. Washington, D.C.: National Aeronautics and Space Administration, 1993: 1-57.

[2] 刘瑞同, 王鑫伟, 荚淑萍. 碳纤维-环氧树脂波纹梁吸能能力的试验研究[J]. 航空学报, 2001, 23(1): 59-61. LIU R T, WANG X W, JIA S P. Effect of trigger geometry on energy absorption of composite waved-beams[J]. Acta Aeronautica et Astronautica Sinica, 2001, 23(1): 59-61 (in Chinese).

[3] 龚俊杰, 王鑫伟. 复合材料波纹梁吸能能力的数值模拟[J]. 航空学报, 2005, 26(3): 298-302. GONG J J, WANG X W. Numerical simulation of energy absorption capability of composite waved beams[J]. Acta Aeronautica et Astronautica Sinica, 2005, 26(3): 298-302 (in Chinese).

[4] ZHOU W Y, CRAIG J, HANAGUD S. Crashworthy behavior of graphite/epoxy composite sine wave webs[C]//32nd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference. Reston: AIAA, 1991: 1618-1626.

[5] INDERMUEHLE K, BARNES G, NIXON S, et al. Simulating composites crush and crash events using ABAQUS[C]//50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference. Reston: AIAA, 2009: 1-12.

[6] NAGEL G M, THAMBIRATNAM D P. A numerical study on the impact response and energy absorption of tapered thin-walled tubes[J]. International Journal of Mechanical Sciences, 2004, 46(2): 201-216.

[7] SANTOSA S, BANHART J, WIERZBICKI T. Experimental and numerical analyses of bending of foam-filled sections[J]. Acta Mechanica, 2001, 148(1-4): 199-213.

[8] TAN X C, CHEN X G. Modelling energy absorption in textile composite cellular structures[C]//49th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference. Reston: AIAA, 2008: 1-12.

[9] 倪先平, 王永亮, 荚淑萍, 等. 直升机机身下部复合材料典型结构耐坠特性研究[J]. 复合材料学报, 2003, 20(4): 51-57. NI X P, WANG Y L, JIA S P, et al. Analysis of crash impact behavior of typical composite components of helicopter bottom structure[J]. Acta Materiae Compositae Sinica, 2003, 20(4): 51-57 (in Chinese).

[10] 王志瑾, KHALIULIN V I. 皱褶结构芯格构型的几何设计方法[J]. 南京航空航天大学学报, 2002, 34(1): 6-11. WANG Z J, KHALIULIN V I. Geometry design method of folded structure[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2002, 34(1): 6-11 (in Chinese).

[11] 曾会华, 徐庆华. 皱褶芯材结构的几何设计与研究[J]. 内江科技, 2009, 30(3): 84. ZENG H H, XU Q H. Geometry design and study of folded core structure[J]. Magazine of Neijiang Science, 2009, 30(3): 84 (in Chinese).

[12] 张慧, 王志瑾. 复合材料层合板皱褶芯材当量力学性能研究[J]. 江苏航空, 2012, 1(S1): 133-136. ZHANG H, WANG Z J. Equivalent mechanical properties study of composite folded core sandwich structure[J]. Jiangsu Aviation, 2012, 1(S1): 133-136 (in Chinese).

[13] HEIMBS S, MIDDENDORF P, KILCHERT S, et al. Experimental and numerical analysis of composite folded sandwich core structures under compression[J]. Applied Composite Materials, 2007, 14(5-6): 363-377.

[14] HEIMBS S, CICHOSZ J, KLAUS M, et al. Sandwich structures with textile-reinforced composite foldcores under impact loads[J]. Composite Structures, 2010, 92(6): 1485-1497.

[15] HEIMBS S, MEHRENS T, MIDDENDORF P, et al. Numerical determination of the nonlinear effective mechanical properties of folded core structures for aircraft sandwich panels[C]//6th European LS -DYNA Users’ Conference. Sweden: Gothenburg, 2007: 29-30.

[16] BARANGER E, GUIDAULT P A, CLUZEL C. Numerical modeling of the geometrical defects of an origami-like sandwich core[J]. Composite Structures, 2011, 93(10): 2504-2510.

[17] 方开泰, 王元. 数论方法在统计中的应用[M]. 北京: 科学出版社, 1996: 222-224. FANG K T, WANG Y. Application of the number theory in statistics[M]. Beijing: Science Press, 1996: 222-224 (in Chinese).

[18] 马兆允, 徐亚栋. 多项式响应面方法在结构近似分析中的应用[J]. 科技资讯, 2006, 33: 111-112. MA Z Y, XU Y D. Application of polynomial response surface method in structural approximate analysis[J] . Science & Technology Information, 2006, 33: 111-112 (in Chinese).

[19] DEB K, AGRAWAL S, PRATAP A, et al. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II[J]. Lecture Notes in Computer Science, 2000, 1917: 849-858.

[20] FISCHER S, DRECHSLER K, KILCHERT S, et al. Mechanical tests for foldcore base material properties[J]. Composites Part A: Applied Science and Manufacturing, 2009, 40(12): 1941-1952.

[21] HONG S T, PAN J, TYAN T, et al. Quasi-static crush behavior of aluminum honeycomb specimens under compression dominant combined loads[J]. International Journal of Plasticity, 2006, 22(1): 73-109.

周华志 男， 博士研究生。主要研究方向： 飞行器结构设计、 复合材料结构优化设计、 新型轻质结构设计。

Tel: 025-84891791

E-mail: 2543436974@qq.com

王志瑾 女， 博士， 博士生导师。主要研究方向： 飞行器结构设计、 复合材料结构优化设计、 热防护结构设计、 新型轻质结构设计。

Tel: 025-84891791

E-mail: zhijin@nuaa.edu.cn

Received： 2015-03-04； Revised： 2015-04-02； Accepted： 2015-06-01； Published online： 2015-06-29 13:49

URL： www.cnki.net/kcms/detail/11.1929.V.20150629.1349.002.html

Foundation items： Funding of Jiangsu Innovation Program for Graduate Education (KYLX_0298); the Fundamental Research Funds for the Central Universities

*Corresponding author. Tel.： 025-84891791 E-mail: zhijin@nuaa.edu.cn

Analysis of energy absorption capability of M-type folded coresandwich structure

ZHOU Huazhi, WANG Zhijin*

CollegeofAerospaceEngineering,NanjingUniversityofAeronauticsandAstronautics,Nanjing210016,China

The folded core sandwich panel, as an advanced sandwich composite structure, is a new type sandwich structure and has a lot of advantages. In this paper, a finite element model of the folded core with imperfections is set up to study the relation between the energy absorption coefficient and the geometric characteristics of M-type folded core. The result of the dynamic compression test simulation agrees well with the experimental result in the CELPACT program. When compared with the ability of honeycomb core, the folded core shows great advantages in energy absorption ability. The energy absorption coefficient of the folded core is more than twice the coefficient of the honeycomb core. The relations between the energy absorption ability and the geometric characteristics of M-type folded core are studied with the help of the response surface method. Finally, an optimization based on the Latin hypercube sampling (LHS) and multi-objective non-dominated sorting genetic algorithm (NSGA-II) is proceeded to obtain the folded core with the best energy absorption ability.

folded core sandwich panel; crashworthiness; energy absorption coefficient; response surface; optimization

2015-03-04；退修日期：2015-04-02；录用日期：2015-06-01； < class="emphasis_bold">网络出版时间：

时间： 2015-06-29 13:49

www.cnki.net/kcms/detail/11.1929.V.20150629.1349.002.html

江苏省普通高校研究生科研创新计划资助项目(KYLX_0298)； 中央高校基本科研业务费专项资金

.Tel.： 025-84891791 E-mail: zhijin@nuaa.edu.cn

周华志， 王志瑾． M-型皱褶芯材夹层板吸能性能研究[J]． 航空学报, 2016, 37(2): 579-587. ZHOU H Z, WANG Z J. Analysis of energy absorption capability of M-type folded core sandwich structure[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(2): 579-587.

http://hkxb.buaa.edu.cn hkxb@buaa.edu.cn

10.7527/S1000-6893.2015.0168

V214.9

： A

： 1000-6893(2016)02-0579-09

*