DLR-F6/FX2B翼身组合体构型高阶精度数值模拟

王运涛， 孟德虹， 孙岩， 张玉伦， 李伟

1.中国空气动力研究与发展中心 计算空气动力研究所， 绵阳 621000 2.中国空气动力研究与发展中心 空气动力学国家重点实验室， 绵阳 621000

DLR-F6/FX2B翼身组合体构型高阶精度数值模拟

王运涛1， 孟德虹1， 孙岩2,*， 张玉伦1， 李伟1

1.中国空气动力研究与发展中心 计算空气动力研究所， 绵阳 621000 2.中国空气动力研究与发展中心 空气动力学国家重点实验室， 绵阳 621000

基于雷诺平均Navier-Stokes(RANS)方程和结构网格技术，采用五阶空间离散精度的加权紧致非线性格式(WCNS)和剪切应力输运(SST)两方程湍流模型，开展了DLR-F6和DLR-F6_FX2B 2种翼身组合体构型的高阶精度数值模拟，计算外形来自AIAA 第三届阻力预测研讨会。主要目的是确认WCNS模拟跨声速典型运输机构型和预测局部构型变化引起的气动特性变化量的能力。在固定升力系数条件下，采用粗、中、细3套网格开展了网格收敛性研究，从气动力系数、压力系数分布、表面流态等方面研究了网格规模对DLR-F6和DLR-F6_FX2B翼身组合体数值模拟结果的影响；采用中等网格开展了来流迎角对2种翼身组合体气动特性的影响研究。通过与National Transonic Facility (NTF)的试验结果和CFL3D的计算结果对比，表明采用高阶精度计算方法得到了网格收敛的数值模拟结果，较好地模拟了DLR-F6翼身组合体局部修型引起的微小气动特性变化和翼身结合部流动特性的差异。

RANS方程； WCNS； 流场模拟； 网格密度； 气动特性

基于雷诺平均Navier-Stokes(RANS)的数值模拟技术已经成为气动设计工作者手中重要的设计工具，但其数值模拟运输机高速巡航构型阻力系数的可信度水平依然有待进一步提高，数值模拟结果受网格密度、湍流模型、计算方法影响较大[1-4]。计算流体力学(CFD)软件和方法的验证与确认工作一直是空气动力学研究的热点之一,其中最具代表性的工作是AIAA组织的系列阻力预测研讨会(DPW I～DPW V)[5-9]、高升力预测研讨会(HiLiftPW I～II)[10]以及欧盟资助的两期欧洲高升力计划(EUROLIFT I～II)[11-12]。以上系列研讨会均通过提供共同研究模型和标准网格，邀请世界范围内或欧盟内部的空气动力学研究机构共同参与CFD的验证和确认工作，其主要目的是评估运输机构型气动特性数值模拟的现状，明确CFD技术下一步发展方向，促进CFD应用水平的提高和相关流动机理研究工作的进展。

DLR-F6翼身组合体构型及其DLR-F6_FX2B修型构型是AIAA DPW III选择的研究模型。文献[13]汇总了来自世界范围的、采用多种网格拓扑结构和多种湍流模型的26组计算结果，通过与NTF(National Transonic Facility)的试验结果相比较，主要结论为数值模拟结果并没有很好地模拟DLR-F6构型局部修型引起的气动特性差量,不同软件的计算结果之间气动数据分散程度较大。文献[13]汇总的数值模拟结果均是采用二阶空间离散精度的方法获得的，基于三阶以上空间离散精度的数值模拟结果尚未见相关报道。文献[14]采用加权紧致非线性格式(WCNS)开展了DLR-F6翼身组合体的数值模拟，计算状态来自AIAA DPW II，计算构型与本文的基本构型相同，但基于平均气动弦长的雷诺数为300万，而本文的计算雷诺数为500万，且更关注DLR-F6翼身组合体局部修型引起的微小气动特性变化。文献[15]采用WCNS和DLR-F6翼身组合体开展了剪切应力输运(SST)湍流模型不同离散精度对数值模拟结果的影响分析。

本文基于RANS方程和结构网格技术，采用五阶空间离散精度的WCNS[16-17]和Menter SST[18]两方程湍流模型，开展了DLR-F6和DLR-F6_FX2B 2种翼身组合体构型的高阶精度数值模拟，重点关注高阶精度数值方法模拟局部构型变化引起的气动特性变化量的能力。在固定升力系数下，采用粗(Coarse)、中(Medium)、细(Fine)3套网格开展了网格收敛性研究，从气动力系数、压力系数分布、表面流态等方面研究了网格规模对2种翼身组合体构型气动特性的影响；采用中等网格开展了来流迎角对2种翼身组合体构型气动特性的影响研究。

1 高阶精度计算方法

任意坐标系下的RANS方程组可分为采用雷诺平均得到的流动控制方程和湍流模型控制方程2个部分。在本文的研究中，流动控制方程对流项离散采用五阶精度的WCNS格式，黏性项的离散采用六阶精度中心格式，边界及近边界条件采用单边四阶精度格式离散；湍流模型采用Menter SST两方程模型，湍流模型及边界条件的离散采用与流动控制方程相同的高阶精度离散方法。以下简单介绍五阶空间离散精度的WCNS格式和四阶精度的边界及近边界格式，详细介绍可参见文献[16]。设网格间距为h，以ξ方向为例， WCNS格式可表示为

四阶精度的边界及近边界格式表示为

2 计算模型与计算网格

DLR-F6翼身组合体是由德国宇航院(DLR)设计的现代运输机典型巡航构型，设计马赫数Ma=0.75, 升力系数CL=0.50，该构型是AIAADPWII的研究模型之一，为了消除翼身结合部的局部分离对数值模拟结果的影响，文献[19]设计了DLR-F6翼身组合体的局部修型构型DLR-F6_FX2B，AIAADPWIII选择了基本构型和修型构型做为研究模型，并将来流雷诺数由3.0×106提高到5.0×106。DLR-F6基本构型及局部修型构型如图1所示，几何参数见表1。风洞试验是在美国NASA的2.5m×2.5mNTF跨声速风洞中完成的，试验结果[20]包括气动特性、压力分布和表面流态等。

本文工作采用的多块对接结构网格由商业软件生成。为了开展网格收敛性研究生成了粗、中、细3套网格，DLR-F6_FX2B构型粗网格的表面网格及局部放大图如图2所示。3套网格的基本参数见表2，其中B.L.为边界层。DLR-F6基本构型的网格拓扑与网格分布与DLR-F6_FX2B构型完全相同，以避免网格因素对数值模拟结果的影响。

图1 DLR-F6和DLR-F6_FX2B翼身组合体构型

Fig.1 DLR-F6 and DLR-F6_FX2B wing-body configuration

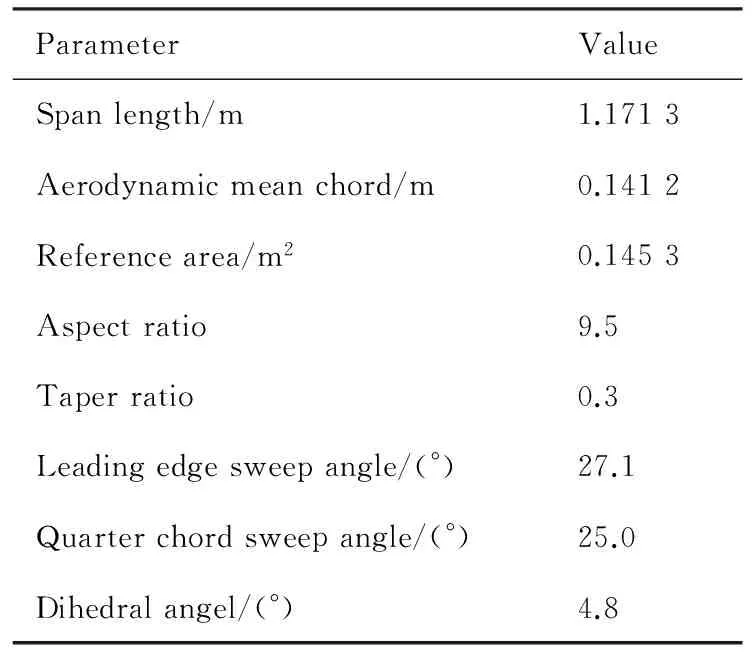
表1 DLR-F6翼身组合体构型基本参数

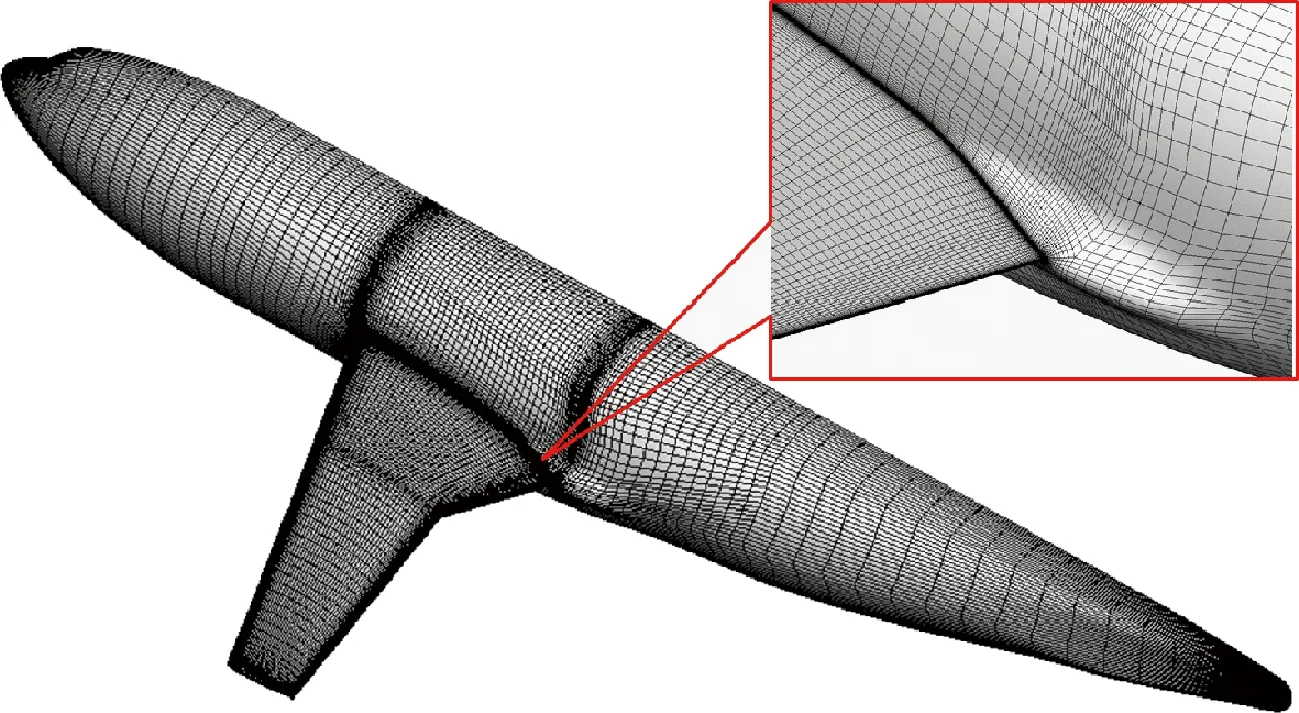
图2 DLR-F6_FX2B翼身组合体构型的表面网格

Fig.2 Surface grid for DLR-F6_FX2B wing-body configuration

表2 DLR-F6_FX2B翼身组合体的网格参数

Table 2 Grid parameters for DLR-F6_FX2B wing-body configuration

ParameterCoarseMediumFineNodenumber3868996922968825125188FirstgriddistanceinB.L./mm0.000600.000400.00027GridnumberinB.L.415373GridratioinB.L.1.2691.2091.147

3 网格收敛性

本节采用粗、中、细3套网格和高阶精度计算方法开展了网格密度对计算结果的影响研究，主要包括气动力系数、表面压力系数和表面流态，计算采用全湍流方式。来流条件为:Ma=0.75，Re=5.0×106。

3.1 气动力系数

表3给出了固定升力系数下(CL=0.500±0.001)，采用粗、中、细3套网格得到的DLR-F6和DLR-F6_FX2B翼身组合体的阻力系数CD、压差阻力系数CDp、摩擦阻力系数CDf和俯仰力矩系数Cm。相应的阻力系数的试验结果通过曲线拟合得到[13]。固定升力系数下，试验得到的DLR-F6翼身组合体及局部修型构型的阻力系数分别为0.027 5±0.000 1和0.027 3±0.000 2，修型前后的阻力系数变化量为0.000 2±0.000 3。由表3 可以看出，本文采用中网格和细网格计算得到的阻力系数相同，且比采用粗网格得到的阻力系数略小。对于DLR-F6/FX2B构型和以附着流动为主的计算状态，阻力系数随网格规模变化不大的事实说明壁面第一层网格距离和边界层内的网格伸展率比网格规模本身对数值模拟结果更重要。固定升力系数下的迎角和俯仰力矩特性随着网格密度的增加均是单调变化的。修型前后，计算得到的阻力系数变化量为0.000 3，在试验结果的误差范围之内。

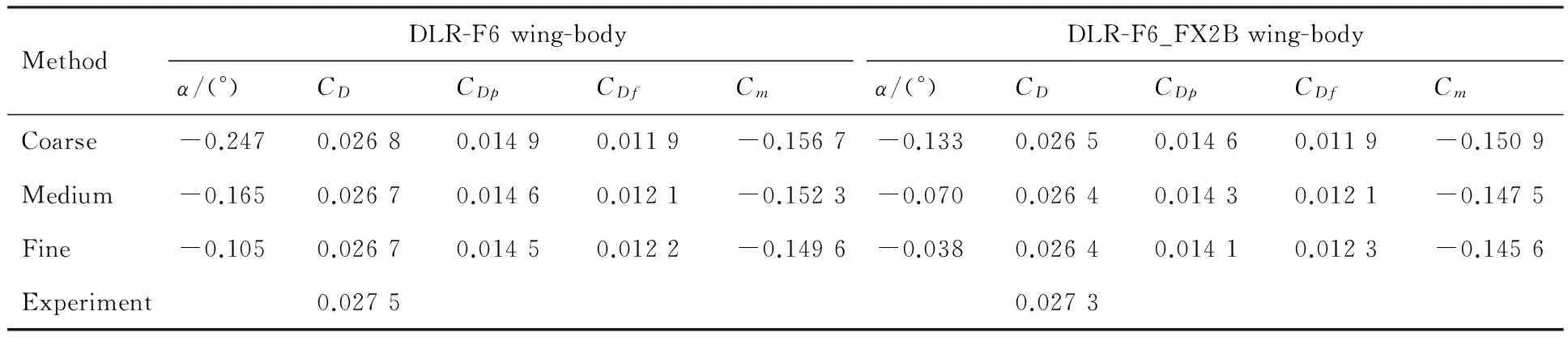
表3 DLR-F6和DLR-F6_FX2B翼身组合体的气动特性 (CL=0.500±0.001)

3.2 表面压力系数

图3给出了DLR-F6_FX2B构型网格密度对机翼3个不同展向站位η=0.239、0.411、0.847表面压力系数Cp的影响。网格密度对机翼中部上表面的激波宽度略有影响(η=0.411)，而对机翼上表面的其他位置和机翼下表面的压力分布基本没有影响。中网格和密网格在不同站位的压力分布具有较好的一致性。网格密度对DLR-F6构型表面压力系数的影响与此类似。

图3 DLR-F6_FX2B不同展向站位的压力系数分布

Fig.3 Pressure coefficient distribution at different spanwise sections of DLR-F6_FX2B

3.3 表面流态

图4给出了DLR-F6构型和DLR-F6_FX2B构型采用不同网格密度得到的翼身结合部上表面极限流线，采用摩擦阻力系数进行物面着色。

图4 上表面极限流线

Fig.4 Streamlines on upper surface

采用不同密度的网格均较好地分辨出了DLR-F6构型翼身结合部后缘的局部分离区(图中红色圆圈内)，随着网格密度增加，翼身结合部后缘局部分离区纵向与横向的宽度略微增加。采用不同密度的网格均较好地显示了DLR-F6构型翼身结合部局部修型的效果，即翼身结合部后缘的局部分离区消失，这是固定升力系数下，DLR-F6_FX2B构型的阻力系数略小于DLR-F6构型的阻力系数的主要原因。

4 气动特性随迎角的变化

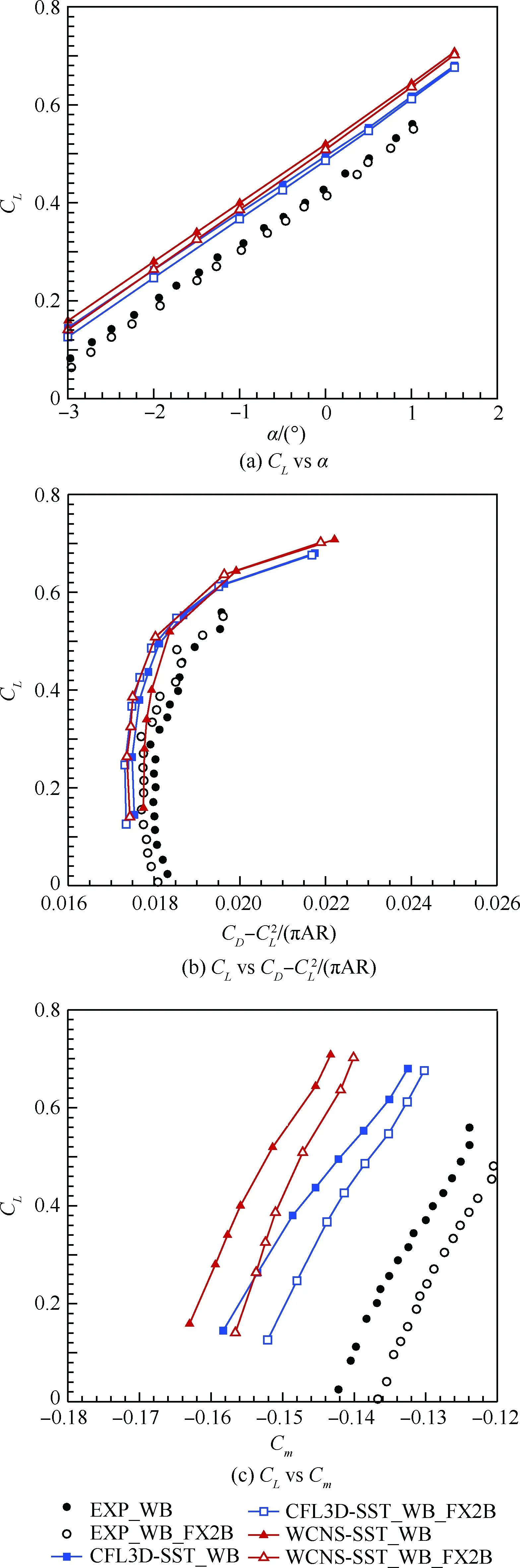
图5 DLR-F6和DLR-F6_FX2B翼身组合体的气动特性

Fig.5 Aerodynamic characteristics of DLR-F6 and DLR-F6_FX2B wing-body configuration

在计算迎角范围内，采用高阶精度计算方法得到的相同迎角下的升力系数略大于CFL3D的计算结果，且均大于试验值；两组计算结果均显示在相同迎角下，局部修型后的升力系数小于修型前的升力系数，这与试验结果的变化趋势是一致的。相同升力系数下，对于DLR-F6构型，本文计算得到的理想阻力系数大于CFL3D的计算结果；对于DLR-F6_FX2B构型，本文计算得到的理想阻力系数则与CFL3D的计算结果相当；采用2种计算方法得到阻力系数均反映出翼身结合部修型后引起的阻力系数减小的趋势，且变化量在升力系数大于0.50后逐渐减少，这与试验结果的变化趋势是一致的。对于相同升力系数下的俯仰力矩系数，本文计算得到的2个翼身组合体构型的低头力矩均大于CFL3D的计算结果；采用2种方法得到的计算结果均反映出修型后的俯仰力矩系数减小，这与风洞试验结果的变化趋势是一致的。根据文献[13]的研究结论，计算模型中没有考虑风洞试验模型的弹性变形是导致升力系数、俯仰力矩系数的计算结果与风洞试验结果之间存在差异的主要原因之一。

5 结 论

1) 在固定升力系数下，采用粗、中、细3套网格和高阶精度计算方法得到了具有网格收敛性的气动力结果；网格分布对机翼中部上表面的激波宽度和翼身结合部后缘局部分离区大小略有影响。

2) 高阶精度的数值模拟结果较好地反映了局部修型引起的气动特性变化量和翼身结合部流动特性的差异。

本文的下一步工作将在计算模型中考虑静气动弹性的影响，进一步开展气动特性的计算与试验结果的对比分析。

[1] SLOTNICK J, KHODADOUST A, ALONSO J, et al. CFD vision 2030 study: A path to revolutionary computational aerosciences: NASA/CR-2014-218178[R]. Washington, D.C.： NASA, 2014.

[2] TINOCO E N, BOGUE D R, KAO T J, et al. Progress toward CFD for full flight envelope[J]. The Aeronautical Journal, 2005, 109(1100): 451-460.

[3] 徐嘉, 刘秋洪, 蔡晋生, 等. 基于隐式嵌套重叠网格技术的阻力预测[J]. 航空学报, 2013, 34(2): 208-217. XU J, LIU Q H, CAI J S, et al. Drag prediction based on overset grids with implicit hole cutting technique[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(2): 208-217 (in Chinese).

[4] KROLL N, BIELER H, DECONINCK H, et al. ADIGMA—A European initiative on the development of adaptive higher-order variational methods for aerospace application[C]//Noteson Numerical Fluid Mechanics and Multidisciplinary Design. Berlin: Springer-Verlag, 2010.

[5] LEVY D W, ZICKUHR T, VASSBERG J C, et al. Summary of data from the first AIAA CFD drag prediction workshop: AIAA-2002-0841[R]. Reston： AIAA, 2002.

[6] LAFLIN K R, KLAUSMEYER S M, ZICKUHR T, et al. Data summary from the second AIAA computational fluid dynamics drag prediction workshop[J]. Journal of Aircraft, 2005, 42(5): 1165-1178.

[7] VASSBERG J C, TINOCO E N, MANI M, et al. Abridged summary of the third AIAA CFD drag prediction workshop[J]. Journal of Aircraft, 2008, 45(3): 781-798.

[8] VASSBERG J C, TINOCO E N, MANI M, et al. Summary of the fourth AIAA CFD drag prediction workshop: AIAA-2010-4547[R]. Reston： AIAA, 2010.

[9] LEVY D W, LAFLIN K R, TINOCO E N, et al. Summary of data from the fifth AIAA CFD drag prediction workshop: AIAA-2013-0046[R]. Reston： AIAA, 2013.

[10] RUMSEY C L, LONG M, STUEVER R A. Summary of the first AIAA CFD high lift prediction workshop: AIAA-2011-0939[R]. Reston： AIAA, 2011.

[11] HEINZ H. Overview about the European high lift research programme EUROLIFT: AIAA-2004-0767[R]. Reston： AIAA, 2004.

[12] RUDNIK R, FRHR.V.GEYR H. The European high lift project EUROLIFT II—Objectives, approach, and structure: AIAA-2007-4296[R]. Reston： AIAA, 2007.

[13] VASSBERG J V, TINOCO E N, MORE M, et al. Comparison of NTF experimental data with CFD predictions from the third AIAA CFD drag prediction workshop: AIAA-2008-6918[R]. Reston： AIAA, 2008.

[14] 王运涛， 孙岩， 王光学, 等. DLR-F6翼身组合体的高阶精度数值模拟[J]. 航空学报， 2015, 36(9): 2913-2919. WANG Y T, SUN Y, WANG G X, et al. High-order accuracy numerical simulation of DLR-F6 wing-body configuration[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(9): 2913-2919 (in Chinese).

[15] 王运涛， 孙岩， 王光学, 等. 高阶精度方法下的湍流生成项对跨声速流动数值模拟的影响研究[J]. 空气动力学学报， 2015, 33(1): 25-30. WANG Y T, SUN Y, WANG G X, et al. Numerical study of the effect of turbulent production terms on the simulation of transonic flows with high-order numerical method[J]. Acta Aerodynamica Sinica, 2015, 33(1): 25-30 (in Chinese).

[16] DENG X G, ZHANG H X. Developing high-order weighted compact nonlinear schemes[J]. Journal of Computational Physics, 2000, 165(1): 24-44.

[17] DENG X G, MIN R B, MAO M L, et al. Further studies on geometric conservation law and application to high-order finite difference scheme with stationary grid[J]. Journal of Computational Physics, 2013, 239: 90-111.

[18] MENTER F R. Two-equation eddy-viscosity turbulence models for engineering application[J]. AIAA Journal, 1994, 32(8): 1598-1605.

[19] VASSBERG J C, SCLAFANI A J， DEHAAN M A. A wing-bodyfairing design for the DLR-F6 model: A DPW-III case study: AIAA-2005-4730[R]. Reston： AIAA, 2005.

[20] GATLIN G M, RIVER S M, GOODLIFF S L, et al. Experimental investigation of the DLR-F6 transport configuration in the National Transonic Facility: AIAA-2008-6917[R]. Reston： AIAA, 2008.

[21] TINOCO E N, VENKATAKRISHNAN C, WINKLER C. Structured and unstructured solvers for the third AIAA CFD drag predicition workshop[J]. Journal of Aircraft, 2008, 45(3): 738-749.

王运涛 男， 博士， 研究员， 博士生导师。主要研究方向： 计算空气动力学。

Tel: 0816-2463037

E-mail: ytwang@skla.cardc.cn

孟德虹 男， 硕士， 助理研究员。主要研究方向： 计算空气动力学。

Tel: 0816-2463062

E-mail: mdh157@163.com

孙岩 男， 博士研究生。主要研究方向： 计算流体力学。

Tel: 0816-7067915

E-mail: supersunyan@163.com

张玉伦 男， 硕士， 副研究员。主要研究方向： 流体力学。

Tel: 0816-2463062

E-mail: ylzhang@skla.cardc.cn

李伟 男， 硕士， 研究实习员。主要研究方向： 计算空气动力学。

Tel: 0816-2463062

E-mail: kuaileo6@163.com

Received： 2015-03-10； Revised： 2015-04-07； Accepted： 2015-05-06； Published online： 2015-05-15 13:17

URL： www.cnki.net/kcms/detail/11.1929.V.20150515.1317.002.html

Foundation item： National Key Basic Research Program of China (2014CB744803)

*Corresponding author. Tel.： 0816-7067915 E-mail: supersunyan@163.com

High-order accuracy numerical simulation of DLR-F6/FX2Bwing-body configuration

WANG Yuntao1, MENG Dehong1, SUN Yan2,*, ZHANG Yulun1, LI wei1

1.ComputationalAerodynamicsInstitute,ChinaAerodynamicsResearchandDevelopmentCenter,Mianyang621000,China2.StateKeyLaboratoryofAerodynamics,ChinaAerodynamicsResearchandDevelopmentCenter,Mianyang621000,China

Based on the Reynolds-averaged Navier-Stokes (RANS) equations and structured grid technology, the fifth-order weighted compact nonlinear scheme (WCNS) and shear stress transport (SST) turbulence model are adopted to simulate DLR-F6 wing-body and FX2B fairing configuration from the third AIAA CFD drag prediction workshop. The main purpose of the present work is to further validate the ability of WCNS in the simulation of transonic problems and the prediction of aerodynamic characteristic variation due to tiny variation of the configuration. The grid convergence study is performed with coarse, medium and fine grid systems at fixed lift coefficient, and the effects of grid density on the simulation of DLR-F6 with and without FX2B fairing are studied from the aspects of aerodynamic coefficients, pressure distribution and flow pattern on the surface. The variations of aerodynamic characteristics with angles of attack are performed with the medium grid system. Compared to the experimental data from the National Transonic Facility (NTF)and CFL3D numerical results, the numerical simulation indicate that grid convergence results are obtained with the high-order numerical method; the small incremental aerodynamic characteristics and the local flow difference at the wing-body junction with and without FX2B fairing can be predicted reasonably.

RANS equations; WCNS; flow simulation; grid density; aerodynamic characteristics

2015-03-10；退修日期：2015-04-07；录用日期：2015-05-06； < class="emphasis_bold">网络出版时间：

时间： 2015-05-15 13:17

www.cnki.net/kcms/detail/11.1929.V.20150515.1317.002.html

国家重点基础研究发展计划 (2014CB744803)

.Tel.： 0816-7067915 E-mail: supersunyan@163.com

王运涛， 孟德虹， 孙岩, 等． DLR-F6/FX2B翼身组合体构型高阶精度数值模拟[J]． 航空学报, 2016, 37(2): 484-490. WANG Y T, MENG D H, SUN Y，et al. High-order accuracy numerical simulation of DLR-F6/FX2B wing-body configuration[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(2): 484-490.

http://hkxb.buaa.edu.cn hkxb@buaa.edu.cn

10.7527/S1000-6893.2015.0124

V211.7

： A

： 1000-6893(2016)02-0484-07

*