涡破裂诱导的垂尾抖振气动弹性分析
赵子杰, 高超, 张正科西北工业大学 航空学院, 西安 710072
涡破裂诱导的垂尾抖振气动弹性分析
赵子杰, 高超, 张正科*
西北工业大学 航空学院, 西安 710072
通过试验方法分析了三角翼前缘分离涡与垂尾抖振之间的关系,深入研究了尾迹流动对垂尾抖振各阶模态的激励作用。计算得到了垂尾模型固有频率及各阶模态。在风洞试验中,应用激光片光烟流场显示技术,得到了三角翼模型在风速为30 m/s下,各迎角的涡结构;使用加速度传感器测量了垂尾翼根和翼梢的抖振响应;使用热线风速仪测量了垂尾翼根和翼梢位置的脉动速度分量。结果表明:前缘涡破裂后产生的高湍流度的尾迹是垂尾抖振的直接原因,抖振边界与涡破裂的强度和位置有关;涡破裂后尾迹与垂尾产生共振,使得抖振加速度响应频率与垂尾固有频率一致;涡破裂后,在较小迎角下,尾迹对垂尾的高频振动模态的激励较为明显,在较大迎角下,涡破裂流动对垂尾低频振动模态的激励加强了。
垂尾抖振; 大迎角; 前缘涡; 抖振加速度; 振动模态
现代战斗机多采用双垂尾布局设计,这种设计可以提高飞机的机动性和隐身性,同时有一定的战损冗余。同时,现代飞行器要实现大迎角飞行,超机动飞行和改善过失速机动性能,常使用边条翼或鸭翼,这主要是利用分离涡产生非线性涡升力及协调亚、跨、超声速不同速度范围对机翼平面形状要求的矛盾。然而,当飞行器迎角过大时,主翼或边条翼产生的分离涡会在到达垂尾前破裂,当垂尾浸润在高湍流度的尾迹中时,在这种强非线性扰动的作用下,垂尾抖振就被激励出来, 垂尾抖振问题是一种典型的考虑气动弹性耦合效应的随机振动问题[1-2]。强度较弱的抖振会引起垂尾结构疲劳,缩短使用寿命,严重的抖振会导致垂尾结构的破坏[3]。
1930年7月21日在英国Kent郡Moephan坠毁的一架容克斯F-13(Junkers F 13)航空运输机,拉开了此类问题研究的序幕。随后的研究指出,造成飞机失事的原因是由于尾翼严重抖振造成的结构失效[4]。1970年至1980年,F-14、F-15、F-16和F-18等一批现代高性能战斗机开始在美国空军和海军中服役。此类战斗机,由于机翼较薄并拥有尖拱状的机身前体,在进行大迎角高机动飞行时,涡流提供了很大一部分气动载荷[5-7],当机身前体主翼及边条的分离涡破裂后,垂尾常需要承受较高的抖振载荷。F-18“大黄蜂”型战斗机,是一种典型的采用双垂尾大后掠边条翼的战斗机,这种布局使得F-18型战斗机具有极佳的大迎角飞行性能。F-18的边条翼使大黄蜂在作大迎角机动时能拉出涡流,迅速地填充到机翼背风面,改善飞机的飞行性能。由于边条翼前缘涡(边条涡)的强劲表现,使得F-18战斗机的垂尾抖振也成为一个严重的问题。以上的特点使F-18型战斗机成为研究垂尾抖振的典型模型。Lee等[8]早期的研究表明, 当前缘边条翼的分离涡在垂尾之前破裂后,尾迹会形成强湍流流动,尾迹的随机脉动压力会激起垂尾结构的强迫振动。随后世界各国装备有该型飞机的国家均对此问题进行了研究。美国国家航空航天局(NASA)最早开展了“高阿尔法计划(High Alpha Technology Program)”,并对F-18型战斗机进行了飞行试验[6];此后,澳大利亚[9],英国[10],加拿大[11-12]和美国[13-15]联合开展了研究项目TTCP(The Technical Cooperation Program)[16]对F-18型战斗机进行了大量的风洞试验,并对其在大迎角下的抖振特性和抖振机理进行了深入探讨。其风洞试验与飞行试验的结果吻合很好,试验测得F-18战斗机垂尾抖振一阶弯曲模态的频率为16.7 Hz,一阶扭转模态的频率为46.7 Hz,且抖振频率不随动压和迎角变化,但垂尾不同位置的加速度变化与迎角有关,其研究成果被用于F-18E/F型的改进。目前最新的关于F-18型战斗机垂尾抖振的研究多集中在数值模拟方面[17-18]。另外,并不是所有的垂尾抖振都起因于边条涡破裂,F-15的垂尾抖振就是由于主翼涡破裂引起的[7, 19]。近年来随着美国第五代战斗机的大批服役,关于F-22型[20-21]和F-35型[22]战斗机垂尾抖振特性的研究也引起了国外学者的重视。
在涡流场作用下的垂尾抖振特性及机理研究方面,Wentz[23]对1∶48的F/A-18飞机模型进行的垂尾表面热膜和流场显示水洞试验表明,垂尾表面湍流度随迎角的增大而升高;抖振的发生与边条涡破裂密切相关,而且涡破裂与垂尾是否安装无关。进一步的研究表明边条涡破裂后形成的大范围的非定常尾迹是垂尾抖振的主要诱因,其中黏性对垂尾表面脉动压力的影响不大,不同雷诺数、不同马赫数下垂尾抖振的特性基本一致,水洞试验、风洞试验和自由飞试验的结果吻合很好[24-25]。Mayori和Rockwell[26]使用了一个简化模型来研究抖振的成因,模型由一个三角翼和一块平板组成,三角翼用于产生一个沿流向的涡,然后将平板置于涡破裂后的尾迹中,同时使用粒子图像测速(Particle Image Velocimetry, PIV)法测量沿流向不同截面的涡流场。结果表明,涡破裂后的下游尾迹随时间呈现大范围的波动和变形,当尾迹通过平板时,会分裂成两部分,且同时远离平板对称面,平板附近的涡流场呈明显的非定常。事实上,垂尾抖振与许多不稳定性有关: 涡核的非周期运动[27];前缘涡的螺旋变形与螺旋形破裂[28-29];涡破裂后,尾迹沿流向的高湍流度流动[30]。Kim等[31]使用一个三角翼和垂尾的组合模型,进行了PIV水洞试验。结果显示垂尾的抖振载荷不仅与前缘涡有关,而且与前缘涡与垂尾相互作用形成的二次涡有密切的联系。此后Kim等[32]还对该模型的PIV试验结果进行了本征正交分解(Proper Orthogonal Decomposition, POD),得到了占总流动能量79.56%的前40阶的流场结构,由此也可看出,前缘涡破裂后的尾迹是强湍流、非定常并包含有许多不同尺度涡结构的流动,更适于用统计学方法进行分析。Hill等[33]对一个三角翼后安装了一对垂尾的模型进行了风洞试验,试验测量了不同风速下垂尾表面的脉动压力,绘制了表面压力云图,同时给出了脉动压力的频率响应。李劲杰等[34]也在风洞中测量了两种不同形状的边条翼布局的双垂尾抖振模型抖振特性,对模型的抖振响应进行了分析,讨论了分离涡对抖振特性的影响。涡核破裂现象是一种明显的产生湍流的现象, 它可以使层流变成湍流,在各种高强度的湍流成分中, 包含着准周期的频率成分,有人预测湍流中的准周期成分是造成机翼及尾翼抖振的主要原因[35]。
本文通过流场显示和三角翼表面压力测量试验,研究三角翼前缘涡破裂与垂尾抖振的关系。同时测量涡破裂后尾迹的频率特性和垂尾不同位置的频率响应,深入研究垂尾的气动弹性响应随迎角的变化。目的是为进一步研究垂尾抖振与涡破裂后流场之间的关系,深入探讨抖振形成的机理。考虑到前缘涡破裂与垂尾抖振对雷诺数并不敏感[35],试验只选取了一个风速(U∞=30 m/s)。
1 试验模型


图1 模型几何外形及流场显示位置剖面图
Fig.1 Model geometry and flow visualization locations
模型在风洞中安装时,为避免风洞洞壁附面层的影响,三角翼半模安装在高出风洞底部100 mm 的端板上(见图2),端板厚15 mm,使用亚克力板(Polymethylmethacrylate, PMMA)制作,端板与风洞下壁面平行。主翼与风洞下壁面及端板垂直,端板中间有一个圆形的转盘,主翼固定在该转盘上,由转盘转动来实现迎角的变化。垂尾与连接杆固定,与主翼垂直,与端板平行,垂尾距三角翼翼根(三角翼垂直对称面)为h=76 mm。连接杆牢固的固定在主翼背风面,三角翼与连接杆的强度与刚度都远远超过垂尾部分,试验时,只考虑垂尾的抖振响应。

图2 试验设置示意图
Fig.2 Sketch of experimental setup
在激光片光烟流场显示试验中,共测量了三角翼上4个位置的流场,分别位于x1/Cw=40%、x2/Cw=68.5%、x3/Cw=81%和x4/Cw=97.2%处(对应图1中Location 1、Location 2、Location 3和Location 4)。三角翼上安装了两排测压孔,分别位于x2/Cw=68.5%和x4/Cw=97.2%处。
另外,端板前缘使用MSE(Modified Super Ellipse)外形,外形由式(1)给出。这种外形设计最早由Lin等[36]提出,这样的设计可以最大程度地避免由前缘逆压梯度造成的分离,并沿端板前缘向下游提供一个可接受的压力梯度场,从而使得对端板层流附面层的扰动降到最低,延长层流附面层的长度。
(1)
式中:AR为曲率;bh为椭圆的短轴;x为坐标主方向;幂指数m(x)和n由式(2)给出,即
(2)
使用三角翼产生的前缘分离涡来模拟战斗机的边条涡,通过研究前缘涡与垂尾相互作用的物理过程(如图3所示),探索垂尾的气动弹性特性,研究抖振产生的机理,是本文的目的,使用简化的模型可去除不必要的飞机外形的影响。

图3 试验原理简图
Fig.3 Schematic diagram for experiments
2 试验设备与测量方法
试验是在低速风洞进行。试验段尺寸为0.6 m×0.6 m×2 m,风速范围为1.5~90.0 m/s,湍流度为0.15%。本次试验模型迎角范围为0°~34°,风速为30 m/s。
三角翼前缘涡的发展变化及最终破裂的过程由烟流激光片光显示技术记录。激光器使用美国COHEREN Genesis MX系列半导体激光器,最大输出功率为3.3 W,试验中,在不同位置剖面,激光器始终与三角翼垂直。发烟器使用美国Concept Smoke System ViCount 1300系统,发烟剂为矿物油混合物,烟雾粒子直径为 0.2~0.3 μm,对流体有很好的跟随性且对激光有较好的反射性。发烟管位于端板前缘,正对模型头部迎风面,出口速度不大于0.5 m/s。当模型有迎角时,烟流可沿三角翼前缘向背风面绕流,形成清晰的前缘涡。激光片光照片由尼康D800相机拍摄。
压力采集系统采用美国Pressure Systems DTC Initium压力采集单元,采样频率为650 Hz,精度为±1 Pa。
试验还用美国DANTEC StreamLine System 热线风速仪(CTA)同时测量了三角翼在不同迎角下的尾迹脉动频谱特性。采样速率为10 kHz,每个试验状态采集6 s。热线支架在风洞中的安装和与三角翼的空间关系如图4所示。为避免支架脱涡引起的颤振,热线支架安装在一个有对称翼型外形的移测机构上。热线探头正对来流,并可在水平和垂直方向上移动。本次试验中,为测量三角翼尾迹对垂尾的影响,热线探头的高度与垂尾所在高度一致,并在垂尾所在高度平面内,沿虚拟的“垂尾”翼根到翼梢移动(如图5所示)。

图4 在风洞中热线风速仪探头及支架的安装
Fig.4 Hot-wire anemometer and bracket setup in wind tunnel
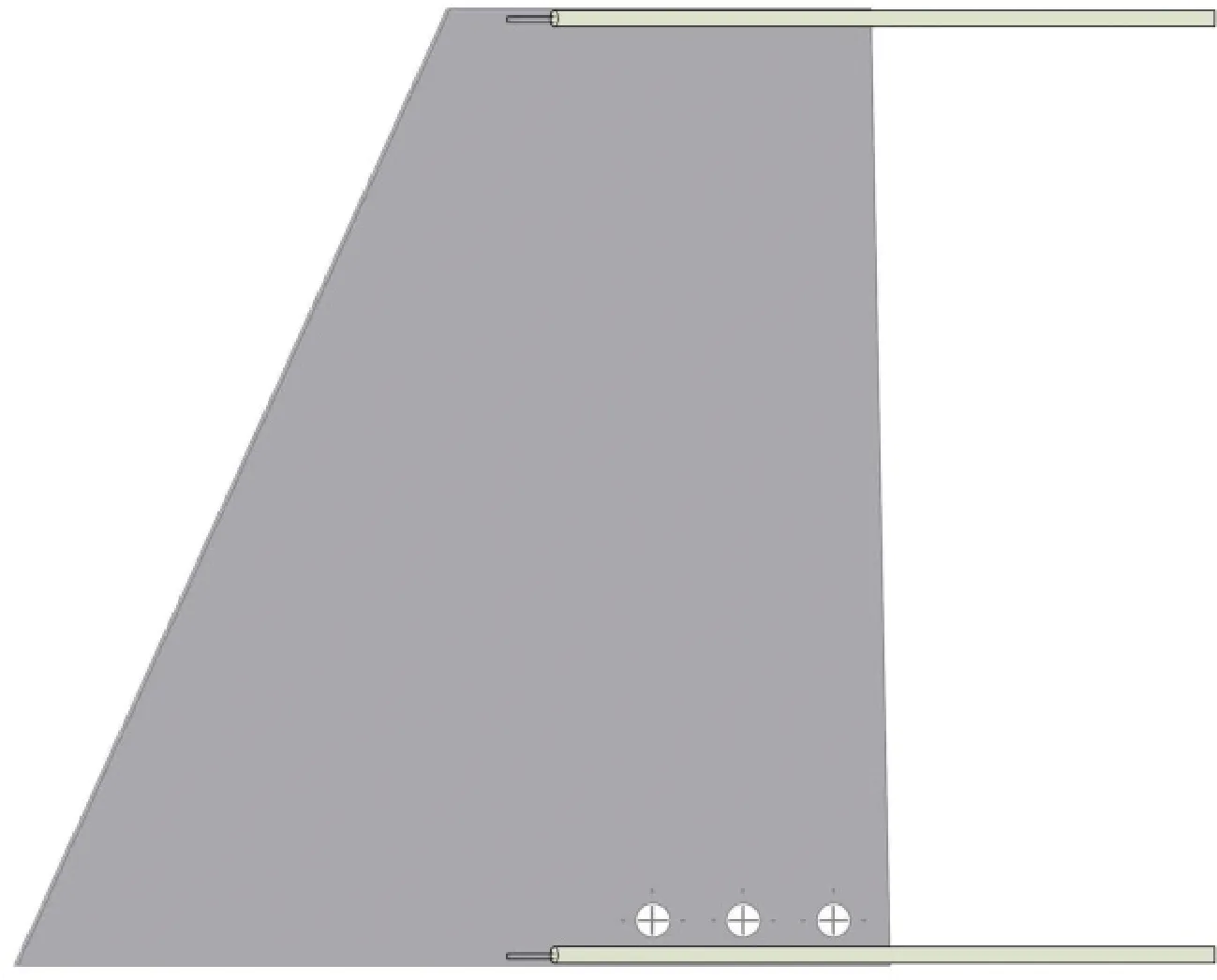
图5 热线探头测量位置示意图
Fig.5 Hot-wire probe measurement locations
两个加速度计分别安装在垂尾翼梢后缘和翼根前缘,用以测量垂尾不同位置的加速度。加速度计在垂尾上的安装位置如图6所示。采用美国PCB PIEZOTRONICS 352a24型加速度计,测量范围为±50g,精度为0.000 2gRMS,频率范围为1~8 000 Hz。加速度计使用专用胶粘在安装位置,迎风面做流线化处理。该型加速度计重约1 g,对结构的质量分布影响基本可以忽略。

图6 在风洞中加速度计的安装
Fig.6 Accelerometers setup in wind tunnel
3 垂尾固有频率及模态分析
垂尾结构固有模态的计算用ANSYS14.0。垂尾建模时使用笛卡儿坐标系(如图7所示),用z表示垂直翼面方向的位移,则模态振型与位移之间的关系可以表示为[37]
(3)
式中:fi(x,y)为结构的第i阶正则模态振型;qi(t)为结构的第i阶模态位移向量;N为模态阶数。考虑系统的动力学方程:
(4)
式中:对于第i阶模态, Mi为系统的质量矩阵;Ci为阻尼矩阵;Ki为刚度矩阵。实际飞行中,li(t)包含两部分,一部分为流体作用于垂尾的刚体载荷(Rigid-bodyLoading)liD(t),另一部为涡破裂后引起的非定常气动载荷(UnsteadyAerodynamicForce)liA(t)。所以li(t)可以写成:
li(t)=liD(t)+liA(t)
(5)
ANSYS14.0workbenchmodal模块对于模态分析有如下假设: 假设材料属性为线弹性;利用小变形理论,且不考虑非线性特征;系统无阻尼;就本垂尾模型而言,结构没有外激励和预应力。基于后两条假设,实际控制方程中,Ci和li(t)为0;合并式(3)和式(4)可得
(6)
式中:ωi为第i阶模态的固有频率。
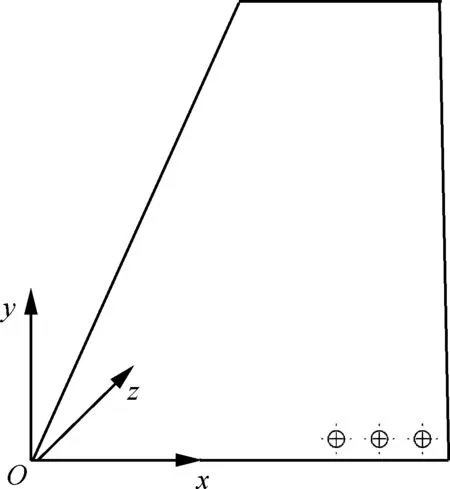
图7 垂尾建模所用坐标系
Fig.7 Coordinate system of vertical tail model
网格划分使用非结构网格,网格拓扑如图8所示,其中模型共采用了18 751个节点,9 091个单元。
模型采用硬铝为材料,计算条件设置:弹性模量为69GPa,密度为2.78×103kg/m3,松泊比为0.33。考虑到模型的实际安装条件,计算的边界条件为垂尾模型翼根后缘设置3个螺孔为固定约束,其余部分为自由变形。
表1为垂尾模型各阶模态的固有频率,图9为垂尾模型前12阶模态振型图。图中第1阶振动模态固有频率为31.97Hz,从对应的振型图中可以看出是垂尾一弯。第2阶模态固有频率为69.56Hz,对应振型图中可以看出为垂尾一扭。

图8 网格拓扑
Fig.8 Mesh topology

表1 各阶模态固有频率

图9 垂尾模型模态振型图
Fig.9 Modal shapes of vertical tail
4 结果与讨论
4.1 烟流场显示
三角翼前缘涡(边条涡)的存在使升力增加,同时它还会提高翼面上附面层的动量,从而增强附面层抗拒逆压梯度的能力,延迟分离,使机翼的失速迎角大大增加[38],不过当迎角大到一定程度,前缘涡会发生破裂,产生包含高湍流度的尾迹流动。本节用烟流技术观察前缘涡的结构演变。
试验记录了0°至34°共15个迎角下若干截面的流场结构,这里只显示14°至24°的结果。图10 给出了模型不同迎角下4个截面位置的流场图。由图10可看出,在迎角α=14°时,三角翼上下表面的压力差为前缘涡提供了很强的能量,使得三角翼前缘涡在4个截面位置结构明显,涡核清晰可见。不过前缘涡的边缘,随着流动向下游发展,开始变得模糊。值得注意的是,在前缘涡和端板壁面之间有一个较亮的区域,在该区域内流速较慢,这是由于端板附面层的影响。当迎角增加到16°时,前缘涡的强度也有所增强,同时三角翼表面的逆压梯度也随迎角增加而增强,截面1至截面3处的涡结构也更加明显,前缘涡的大小也随着迎角的增加而变大,在所有观测位置上,有可分辨的涡核,涡结构未发生破裂,涡核位置也更加远离物面。当迎角继续增加到18°后,涡结构开始变的不稳定。在前3个截面,前缘涡结构依旧清晰,在截面4,涡核变的难以分辨,涡结构发生变形,并开始螺旋型的破裂。在迎角20°时,随着能量不断耗散,前缘涡的破裂位置已提前到截面3。在截面3上,涡核难以分辨,不过此时涡边缘依旧可以分辨,涡结构开始扭曲,到了截面4,已经没有涡核,且无法分辨涡结构,此时的涡结构已完全破裂。在迎角22°时,前缘涡的破裂位置依旧在截面3,不过此时截面3上的涡结构的大小显著大于迎角20°的情况,且边缘变得十分模糊,形状也不规则。截面2上的涡结构也开始发生变形,边缘开始变得模糊,涡核时隐时现。随着迎角增加到24°,前缘涡在截面2的变形愈加明显,且影响范围越来越大,截面3和截面4的涡结构已彻底破裂并迅速扩散,几乎观测不到涡结构的边缘,涡破裂后的影响范围变得很大,整个尾迹区呈现高湍流度的情况。可以推断,此时,若垂尾浸润在尾迹区,作用在垂尾表面的随机脉动压力将变的很强。
图10 三角翼不同迎角各剖面烟流/激光片光涡流场
Fig.10 Smoke/laser sheet vortex structure at each location of delta wing at different angles of attack
总的来讲,在小迎角时(α=14°,16°),前缘涡基本没有发生破裂,当迎角继续增大,前缘涡开始发生破裂,而且其破裂点随迎角的增大不断向上游移动。当迎角增大时,涡破裂后尾迹的扩散范围也不断增大。
4.2 压力测量结果
图11为风速U∞=30 m/s下三角翼上两个不同截面沿展向压力系数Cp的分布,坐标的无量纲化参考长度取三角翼当地半展长。本文主要关心前缘涡破裂前后的流场情况,后缘附近的压力系数分布是关注的重点,因此这里只给出了Location 4 (x4/Cw=97.2%),迎角α=10°~34°的压力系数分布结果。图11(a)和图11(b)是α=10°~20°的压力系数分布结果,由图可以看出,在这一迎角范围内,吸力峰值基本集中在y/Blocal=0.7左右,涡吸力影响的范围在y/Blocal=0.6到y/Blocal=0.9之间一个狭窄的范围内,且Cp的峰值在α=20°时达到最大,这表明三角翼前缘涡在从小迎角增大到α=20°时,主涡强度在增强。当然,Cp峰值不仅与涡强有关,还与涡核距翼面高低位置有关,较高的涡核位置会使得Cp的峰值下降[39]。
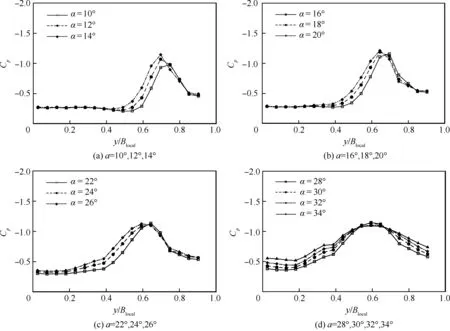
图11 U∞=30 m/s, Location 4 (x4/Cw=97.2%) 处翼面沿展向的压力系数分布
Fig.11 U∞=30 m/s, span wise pressure coefficient distribution at Location 4 (x4/Cw=97.2%)
由图10可以了解到,在这一迎角范围内,涡核位置随迎角的增加而远离翼面,因此,此时Cp峰值的增加可以认为是涡强度增加的结果。随着迎角进一步增加(见图11(c)),压力系数分布有了较明显的变化,Cp变得平坦,未见有明显集中的吸力峰,主涡影响的范围开始扩散,推断此时主涡已经开始破裂。由图11(d)可见,随着迎角增加至28°~34°,吸力峰变得更加平坦,在y/Blocal=0.2到y/Blocal=1.0 的范围内都有明显的负压,同时吸力峰峰值不随迎角变化,推测此时前缘涡已经完全破裂,尾迹影响的范围变得很大。此外,压力系数分布曲线在迎角α=28°~34°时,翼根靠近端板壁面的位置负压上翘,是由于随着前缘涡逐渐远离物面,三角翼在靠近端板的位置又形成了一个二次涡,使得三角翼翼根附近的负压增强。对比流场显示的结果可知,虽然在x4/Cw=97.2%的位置,涡结构已经开始发生破裂,但从压力系数分布的结果来看,涡真正开始破裂的迎角应该在22°附近。
4.3 抖振边界
图12给出了模型垂尾翼梢和翼根加速度均方根值aRMS随迎角变化曲线,由图可以看出,模型垂尾抖振加速度响应在迎角20°之前都很小,迎角超过20°后,翼根和翼梢加速度开始急剧增加,翼梢的加速度响应在α=24°时达到最大,翼根的加速度响应在α=26°时达到最大,之后加速度响应随着迎角继续增加而逐渐减小,加速度减小的变化率明显低于加速度增加的变化率,在迎角到达34°时,垂尾的加速度响应仍较抖振发生前高。

图12 垂尾翼梢和翼根加速度均方根αRMS值随迎角的变化
Fig.12 Acceleration root mean square αRMSof vertical tail tip and root at different angles of attack
对比流场显示的结果,前缘涡在α=18°时开始发生破裂,不过此时,前缘涡仍有较为清晰的边缘,垂尾并未浸润在破裂后的尾迹中,当迎角继续增加至20°后,涡破裂的范围开始不断变大,垂尾受到前缘涡破裂后形成的强湍流流动的激励,开始发生抖振,在翼梢和翼根位置抖振响应最剧烈的迎角分别为24°和26°,当迎角继续增加,由于前缘涡的尾迹的范围越来越大,相应的尾迹中的单位体积内脉动速度分量的能量开始降低,使得垂尾抖振的强度开始下降。
图13为模型垂尾翼梢和翼根湍流度εT随迎角变化曲线,由图可以看出,翼梢位置的湍流度从α=18°时开始增加,此后翼梢位置的湍流度随迎角的增加而持续增加,而翼根位置的湍流度从α=24°时才开始增加。对比激光片光流场显示的结果,前缘涡在α=18°时开始发生破裂,因此垂尾翼梢位置的湍流度开始增加,而此时三角翼前缘分离涡未完全破裂,涡结构仍然远离三角翼面,因此垂尾翼根位置的湍流度并不高。当主涡完全破裂后,尾迹的范围变得很大,因此翼根位置的湍流度也开始急剧增加。
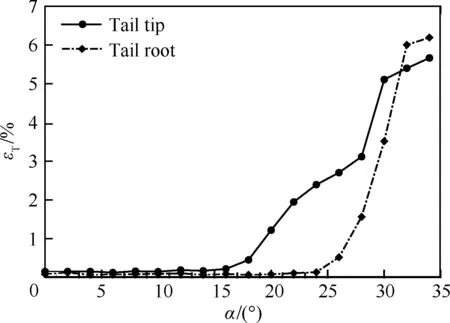
图13 垂尾翼梢和翼根位置尾迹湍流度随迎角的变化
Fig.13 Turbulence intensity in the vicinity of tail tip and tail root within the wake of the main wing at different angles of attack
涡破裂后尾迹中的强湍流成分是造成抖振的主要原因,而对比图12和图13,垂尾附近的湍流度随迎角的增大而不断增大,而垂尾的加速度响应先增加后减小,这看似矛盾的关系需从涡破裂后的尾迹的流动特性和垂尾的结构特性来分析。
4.4 尾迹流场的频率特性与垂尾的气动弹性响应
图14为翼梢加速度频谱图,垂尾抖振各模态的频率不随迎角发生变化,但加速度振幅不同。5个振幅峰值对应的频率如表2所示,对比表1,发现垂尾模型在各迎角下的不同模态的抖振频率与垂尾某几阶模态的固有频率一致,比较图9所示的垂尾各阶结构模态,分别对应第1阶、2阶、3阶、5阶和7阶模态。由此可见,垂尾抖振各模态的频率与外加激励无关,只和垂尾本身的固有频率有关。值得注意的是,抖振响应的频率并不是覆盖了所有结构的固有频率,频率超过660 Hz的振动模态在风洞试验中未测量到。
此外,抖振发生后,迎角较小(α=22°,24°)时,抖振频率在355 Hz时加速度振幅最大,当迎角增加到26°和28°时,加速度振幅的最大峰值已经移到振动频率为152 Hz的模态。且振动频率为68 Hz 的垂尾一扭的加速度振幅也较迎角22°和24°时有了较大增长。随着迎角继续增加,垂尾抖振的垂尾一阶弯矩模态(F=30 Hz)对应的振幅峰值在迎角32°时达到最大。似乎随着迎角的增加,垂尾抖振响应的能量从高频的抖振模态向低频的抖振模态转移。图12中,翼梢加速度均方根偏差在24°时达到最大。垂尾的这种抖振特性与垂尾结构本身有关,垂尾模型类似一端固定的薄板,一般来说低频振动往往伴随较大的位移,而加速度较小,高频振动尽管位移较小,但加速度较大[40]。

表2 垂尾抖振主模态振动频率

图14 不同迎角下翼梢加速度频谱图
Fig.14 Spectrum charts of vertical tail tip acceleration at different angles of attack
图15为不同迎角下垂尾翼梢位置尾迹频谱图。总体而言,尾迹中的脉动速度分量随迎角的增加而增加,这与图13的结论一致。由于前缘涡破裂后会形成许多尺度不一的涡结构,此时的流动事实上是一种准周期的流动[35]。在迎角24°时,流动中的脉动分量集中在频率为150~350 Hz 之间(图15(b)中虚线框所示),当迎角增加至32°后,流动中的脉动分量移至较低的频率范围(10~200 Hz,图15(f)中虚线框所示),对比图14,可以推断,相对较小迎角下的涡破裂流动激励了垂尾的高频振动模态,大迎角下的涡破裂流动激励了垂尾较低频率的振动模态,而高频振动模态下的加速度振幅较大,这就不难理解为什么翼梢加速度均方根值会在迎角24°时达到最大,虽然此时尾迹的湍流度并不是最大。

图15 不同迎角下垂尾翼梢位置尾迹频谱图
Fig.15 Spectrum charts of velocity at vertical tail tip flow field at different angles of attack
5 结 论
1) 垂尾抖振的产生与主翼前缘涡的破裂有着密切的联系,主翼前缘涡破裂后产生的高湍流度的尾迹将垂尾裹挟其中,是垂尾抖振的直接原因;抖振边界不仅与前缘涡是否破裂、破裂程度有关,还与尾迹的扩散范围有关。
2) 主翼前缘涡破裂后的尾迹包含许多尺度不一的涡结构,其中的低频成分与垂尾模型的低频振动模态产生了共振,诱导了抖振的发生;在试验的迎角范围内,当垂尾发生抖振时,其振动频率与垂尾的固有频率一致;垂尾抖振只集中在低频振动模态上。
3) 垂尾翼梢加速度响应随迎角的增加先增大后减小,并在24°时达到最大,而翼梢附近的流场湍流度随迎角增大而持续增大。加速度响应的增长与湍流强度的增长有关,之后减小是由于相对较小迎角下的涡破裂后的尾迹流动增强了垂尾的高频振动模态,大迎角下的尾迹对垂尾较低频率的振动模态激励效果显著,高频振动模态下的加速度较大,而低频振动模态下的加速度较小。
[1] MAYORI A, ROCKWELL D. Interaction of a stream wise vortex with a thin plate: A source of turbulent buffeting[J]. AIAA Journal, 1994, 32(10): 2022-2030.
[2] CANBAZOGLU S, LIN J C, WOLFE S, et al. Buffeting of fin-Distortion of incident vortex[J]. AIAA Journal, 1995, 33(11): 2144-2150.
[3] LEE B H K. Vertical tail buffeting of fighter aircraft[J]. Progree Aerospace Sciences, 2000, 36(3): 193-279.
[4] DUNCAN W, ELLIS D, SCRUTON C. First report on the general investigation of tail buffeting: R&M-1457[R]. British, London: British Aeronautical Research Committee, 1932.
[5] ZIMMERMAN N, FERMAN M, YURKOVICH R N. Prediction of tail buffet loads for design application: AIAA-1989-1378[R]. Reston: AIAA, 1989.
[6] FISHER D F, FRATE J H D, RICHWINE D M. In-flight flow visualization characteristics of the NASA F-18 high alpha research vehicle at high angles of attack: NASA TM 4193[R]. Ames: NASA Ames Research Center Dryden Fligh Research Facility, 1990.
[7] FERMAN M, HUTTSELL L, TURNER E. Experiments with tangential blowing to reduce buffet response on an F-15 model[J]. Journal of Aircraft, 2004, 41(4): 903-910.
[8] LEE B H K, BROWN D, ZGELA M, et al. Wind tunnel investigation and flight tests of tail buffet on the CF-18 aircraft: DTIC Document ADP006218[R]. Canada Ottawa: National Aeronautical Establishment Ottawa, 1990.
[9] MARTIN C, GLAISTER M, MACLAREN L D, et al. Ross F/A-18 1/9th scale model tail buffet measurements: NASA TR-188[R]. Washington, D.C.: NASA, 1991.
[10] MABEY D. Measurements of fin buffeting on an ‘F-18’model and derived interpretive hypothesis: DRA Bedford, Technical Memorandum Aero 2224[R]. British: Bedford, 1991.
[11] LEE B H K, MARINEAU-MES S. Investigation of the unsteady pressure fluctuations on an F/A-18 wing at high incidence[J]. Journal of Aircraft, 1996, 33(5): 888-894.
[12] LEE B H K, MARINEAU-MES S. Load measurements on the leading-edge extension, wing, and body of an F/A-18[J]. Journal of Aircraft, 1998, 35(2): 295-300.
[13] MOSES R W, PENDLETON E. A comparison of pressure measurements between a full-scale and a 1/6-Scale F/A-18 twin tail during buffet: NASA-TM-110282[R]. Washington, D.C.: NASA, 1996.
[14] MEYN L A, JAMES K D. Full-scale wind-tunnel studies of F/A-18 tail buffet[J]. Journal of Aircraft, 1996, 33(3): 589-595.
[15] PETTIT C L, BROWN D L, Banford M P, et al. Full-scale wind-tunnel pressure measurements of an F/A-18 tail during buffet[J]. Journal of Aircraft, 1996, 33(6): 1148-1156.
[16] BEAN D, LEE B H K. Correlation of F/A-18 buffeting from wind-tunnel and flight tests[J]. Journal of Aircraft, 1995, 32(6): 1351-1358
[17] ELMEKAWY A, KANDIL O A, BAYSAL O. F/A-18 twin-tail buffet modeling using non-linear eddy viscosity models: AIAA-2014-2447[R]. Reston: AIAA, 2014.
[18] BARNES C J, VISBAL M R, GORDNIER R E. Investigation of aeroelastic effects in streamwise-oriented vortex/wing interactions: AIAA-2014-1281[R]. Reston: AIAA, 2014.
[19] LEMAY S P, LOVATO J A. Experimental investigation of the vortex-vertical tail interaction on an F-15: AIAA-1994-0070[R]. Reston: AIAA, 1994.
[20] BLACK C L, PATEL S R, ANDERSON W D. Low speed wind tunnel buffet testing on the F/A-22[J]. Journal of Aircraft, 2006, 43(4): 879-885.
[21] BLACK C L, PATEL S R. Buffet fatigue sequence generation from F-22 flight test data using frequency domain methods: AIAA-2007-1765[R]. Reston: AIAA, 2007.
[22] POTOCZSKY A, MOSES R W. An analysis method to predict tail buffet loads of fighter aircraft: AIAA-2005-2291[R]. Reston: AIAA, 2005.
[23] WENTZ W H, Jr. Vortex-fin interaction on a fighter aircraft: AIAA-1987-2474[R]. Reston: AIAA, 1987.
[24] WOLFE S, CANBAZOGLU S, LIN J C, et al. Buffeting fins—An assessment of surface pressure loading[J]. AIAA Journal, 1995, 33(11): 2232-2234.
[25] BEYERS M E, ERICSSON L. Why is LEX vortex breakdown on the F/A-18 configuration insensitive to Reynolds number: AIAA-2001-0690[R]. Reston: AIAA, 2011.
[26] MAYORI A, ROCKWELL D. Interaction of a streamwise vortex with a thin plate—A source of turbulent buffeting[J]. AIAA Journal, 1994, 32(10): 2022-2029.
[27] MENKE M, GURSUL I. Unsteady nature of leading edge vortices[J]. Physics of Fluids, 1997, 9(10): 2960-2966.
[28] GARG A, LEibovich S. Spectral characteristics of vortex breakdown flowfields[J]. Physics of Fluids, 1979, 22(11): 2053-2064.
[29] GURSUL I. Unsteady flow phenomena over delta wings at high angle of attack[J]. AIAA Journal, 1994,32(2): 225-231.
[30] GURSUL I, YANG H. On fluctuations of vortex breakdown location[J]. Physics of Fluids, 1995, 7(1): 229-231.
[31] KIM Y, OZGOREN M, ROCKWELL D. Vortex breakdown-tail interaction[J]. AIAA Journal, 2003, 41(3): 544-549.
[32] KIM Y, ROCKWELL D, LIAKOPOULOS A. Vortex buffeting of aircraft tail: Interpretation via proper orthogonal decomposition[J]. AIAA Journal, 2005, 43(3): 550-559.
[33] HILL B, LEVINSKI O, WATMUFF J. Experimental investigation of generic buffet configuration: AIAA-2006-3485[R]. Reston: AIAA, 2006.
[34] 李劲杰, 杨青, 肖春生. 边条翼布局流场及其双垂尾抖振特性研究[J]. 航空学报, 2006, 27(3): 395-398. LI J J, YANG Q, XIAO C S. Investigation of flow and twin-vertical tail buffet characteristics of leading-edge extension configuration[J]. Acta Aeronautica et Astronautica Sinica, 2006, 27(3): 395-398 (in Chinese).
[35] 吕志咏, 祝立国, 张明禄. 三角翼前缘涡破裂形式及特性研究[J]. 力学学报, 2006, 38(1): 113-118. LU Z Y, ZHU L G, ZHANG M L. Study on some breakdown forms and characteristics of leading edge vortex over delta wings[J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(1): 113-118 (in Chinese).
[36] LIN N, REED H L, SARIC W S. Effect of leading-edge geometry on boundary-layer receptivity to freestream sound[M]//Instability, Transition, and Turbulence. New York: Springer, 1992: 421-440.
[37] 商霖. 基于ANSYS有限元分析的模态质量计算方法[J]. 导弹与航天运载技术, 2011(3): 55-57 . SHANG L. Modal mass computation based on ANSYS finite element analysis[J]. Missiles and Space Vehicles, 2011(3): 55-57 (in Chinese).
[38] GURSUL I. Review of unsteady vortex flows over slender delta wings[J]. Journal of Aircraft, 2005, 42(2): 299-319.
[39] 冯亚南, 刘日之, 邢玉山. 双三角翼外翼前缘钝度对气动特性的影响[J]. 北京航空航天大学学报, 1993(1): 57-61. FENG Y N, LIU R Z, XING Y S. The effect of outboard leading-edge bluntness of doube-delta wing on its aerodynamic characteristics[J]. Journal of Beijing University of Aeronautics and Astronautics, 1993(1): 57-61 (in Chinese).
[40] 李德葆, 陆秋. 工程振动试验分析[M]. 北京: 清华大学出版社, 2004: 250-251. LI D B, LU Q. Analysis of experiments in engineering vibration[M]. Beijing: Tsinghua University Press, 2004:250-251 (in Chinese).
赵子杰 男, 博士研究生。主要研究方向: 跨声速空气动力学, 流动控制。
E-mail: zhaozijie84@gmail.com
高超 男, 博士, 教授, 博士生导师。主要研究方向: 试验空气动力学, 计算空气动力学。
Tel: 029-88491224-22
E-mail: gaochao@nwpu.edu.cn
张正科 男, 博士, 教授, 硕士生导师。主要研究方向: 计算空气动力学。
Tel: 029-88491224-15
E-mail:zkzhang@nwpu.edu.cn
Received: 2015-05-06; Revised: 2015-06-02; Accepted: 2015-06-17; Published online: 2015-07-27 10:31
URL: www.cnki.net/kcms/detail/11.1929.V.20150727.1031.002.html
Foundation item: Key-Levorotary Pre-Research Foundation of China (9140C420301110C42)
*Corresponding author. Tel.: 029-88491224-15 E-mail: zkzhang@nwpu.edu.cn
Aeroelastic analysis of vertical tail buffeting induced byvortex breakdown
ZHAO Zijie, GAO Chao, ZHANG Zhengke*
SchoolofAeronautics,NorthwesternPolytechnicalUniversity,Xi’an710072,China
The relationship between breakdown vortex and vertical tail buffeting is analyzed by experiment. The stimulation effects which the wake of breakdown vortex exerts on various modes of vertical tail buffeting are investigated in detail. The normal modes and natural frequencies of vertical tail model are calculated by numerical method firstly. Then, the vortex structure of delta wing at different angles of attack is recorded by laser sheet flow visualization technique at 30 m/s. The buffeting responses of vertical tail tip and root are measured by accelerometer. The oscillation velocity of the wake is measured using the hot-wire anemometer. The results show that the vertical tail buffeting originates from the breakdown vortex. The buffet boundary is related to the location and intensity of the vortex breakdown. The wake of the vortex resonates with the vertical tail and further reinforces the buffeting phenomenon. As a result, the buffeting frequencies are identical with natural frequencies of the tail structure. The broken-down vortex at relative low angles of attack generates high frequency vibration mode of the vertical tail whereas at high angles of attack gives rise to the low frequency vibration mode.
vertical tail buffeting; high angles of attack; leading edge vortex; buffeting acceleration; vibration mode
2015-05-06;退修日期:2015-06-02;录用日期:2015-06-17; < class="emphasis_bold">网络出版时间:
时间: 2015-07-27 10:31
www.cnki.net/kcms/detail/11.1929.V.20150727.1031.002.html
重点实验室预研基金 (9140C420301110C42)
.Tel.: 029-88491224-15 E-mail: zkzhang@nwpu.edu.cn
赵子杰, 高超, 张正科. 涡破裂诱导的垂尾抖振气动弹性分析[J]. 航空学报, 2016, 37(2): 491-503. ZHAO Z J, GAO C, ZHANG Z K. Aeroelastic analysis of vertical tail buffeting induced by vortex breakdown[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(2): 491-503.
http://hkxb.buaa.edu.cn hkxb@buaa.edu.cn
10.7527/S1000-6893.2015.0188
V211.47; V215.3+6
:A
: 1000-6893(2016)02-0491-13
*

