寿命系数定寿的原理和方法

张福泽空军装备研究院 航空装备研究所， 北京 100076

寿命系数定寿的原理和方法

张福泽*
空军装备研究院 航空装备研究所， 北京 100076

通过对疲劳载荷谱损伤值的研究，发现金属材料的疲劳寿命与疲劳试验载荷谱损伤值成线性关系，即金属材料的疲劳寿命随疲劳试验载荷谱的轻重成线性关系。由此规律推导出寿命系数，通过寿命系数可以降低全尺构件的疲劳试验时间。根据已有的疲劳试验数据研究的寿命系数值显示，在平均谱(疲劳损伤值为50%)基础上加重至58.33%损伤谱可降低全尺寸疲劳试验时间11%，75%损伤谱可降低36%，91.5%损伤谱可降低51%。由此得出：为了减少全尺疲劳试验时间，可以用加重载荷谱进行全尺寸疲劳试验，获得重谱下的寿命，再利用样件的寿命系数将其还原到平均谱下的平均寿命，然后用规范规定的疲劳分散系数除以平均寿命，给出使用寿命。这样既实现了减少疲劳试验时间的目的，又不违背规范规定的疲劳分散数值，使飞机定寿既经济又可靠。

疲劳寿命； 疲劳损伤； 寿命系数； 平均载荷谱； 重谱

众所周知，全尺寸疲劳试验是一项既费时又费钱的工程，如大型运输机的全机疲劳试验要进行12万～24万飞行小时，疲劳试验时间约5～10年，耗资几千万到上亿元人民币。为此，各国“疲劳界”一直在努力寻找解决这个难题的方法，遗憾的是，至今仍没有找到公认有效的方法。

美国在《联合使用规范指南(JSSG—2006)》[1]中规定：用平均谱进行疲劳试验时，试验时间是4倍使用寿命(3倍裂纹形成寿命，1倍裂纹扩展寿命)；用重谱进行疲劳试验时，试验时间由原来的使用寿命4倍降至2倍。中国在《军用飞机结构强度规范(GJB67.6A—2008)》[2]中也如此规定。按“GJB67.6—85”规范理解，用重谱试验可降低2倍的疲劳分散系数。这样规定的原因是什么？至今各国尚未给出合理的解释。

为了探讨上述问题，笔者在文献[3]中，对平均谱和重谱如何影响疲劳分散性的问题进行了深入研究。研究的结论是：在使用载荷下的重谱能降低寿命而不能降低疲劳分散系数。即在使用载荷下，平均谱的疲劳寿命比重谱长，二者的疲劳分散系数相等。这说明在使用载荷下，重谱不能降低疲劳分散系数。由此引起人们对重谱进行疲劳试验可降低试验时间产生疑义。为解决这些问题，本文进行如下研究。

1 研究的总体思路

文献[3]通过论证和试验验证，证明在使用载荷下，用重谱进行疲劳试验，可降低试验寿命，减少试验时间，但分散系数与用平均谱试验的分散系数是相等的。这就是说，重谱不能降低分散系数，用重谱试验仍需用平均谱的分散系数，这显然与文献[1]和文献[2]这2部规范规定的内容相悖。目前，国内外现行规范中的疲劳分散系数取值都是平均谱下寿命的分散系数值[4-5]。为了获得用重谱试验可减少试验时间的优势，又能用上平均谱下寿命的分散系数，本文研究出一种“寿命系数定寿法”来解决这个国际难题。

2 寿命系数定寿法的理论依据

2.1 金属材料的疲劳寿命是试验谱损伤的函数

(1)

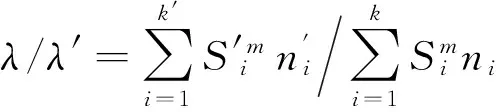
(2)

式(2)表示金属材料在2种谱载荷作用下，寿命比λ/λ′与谱块损伤比的函数关系，即金属材料的疲劳寿命是试验谱损伤的函数。

2.2 金属材料的疲劳寿命与试验谱损伤值呈线性关系

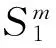
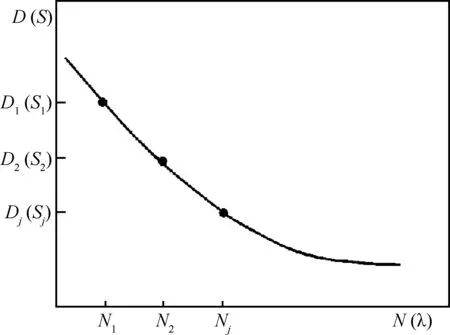
图1 试验的D -N曲线

Fig.1 D -N curve of test

由于D-N曲线即是S-N曲线，因此在中等寿命区，S-N曲线的近似线性关系，即是D-N曲线的近似线性关系。由此得出，金属材料的试验疲劳寿命与试验谱损伤值有近似线性关系。试验验证见本文4.1节。

3 寿命系数定寿法

3.1 寿命系数η

3.2 寿命系数η=L50/L′曲线和取值

由寿命系数η定义，可绘制出推断的寿命系数η与不同损伤谱试验的寿命Li的关系曲线，如图2所示。图2中的纵坐标是寿命系数ηi，横坐标是标准试样在不同损伤谱试出寿命Li。寿命系数η的取值，即是标准试样的平均谱寿命L50除以某一重谱寿命L′的值。

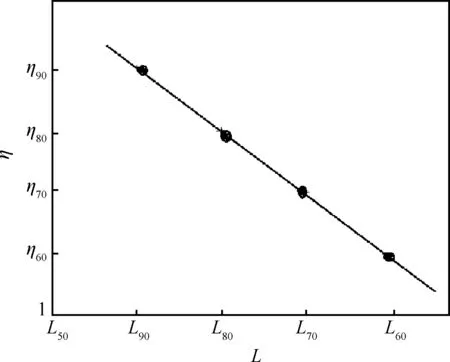
图2 η -L推断原理曲线

Fig.2 Principle η -L curve of deduction

3.3 具体算法

寿命系数定寿法，简单地说，就是用小试样试出寿命系数，来减少大构件疲劳试验时间的方法。

具体讲，寿命系数定寿法，就是通过小试样试出的寿命系数，把大构件用重谱试出的疲劳寿命转换成大构件在平均谱下的疲劳寿命。用算式表示为L50=ηL′。理论和试验都证明，对于试验到破坏的相同构件，重谱试出的寿命L′要低于平均谱的试验寿命L50，重谱试验时间要低于平均谱的试验时间，即重谱可以降低试验时间。由于构件定寿的规范规定，寿命指标是平均谱下的寿命，重谱下的寿命不能作为定寿寿命指标，因此本文通过标准试样试出的寿命系数，把大构件在重谱下的寿命L′转换成大构件在平均谱下的寿命L50，然后再除以规范规定的平均寿命的分散系数，给出高可靠度和高置信度的使用寿命。这样就实现了国内外开始自有全尺寸大构件疲劳试验以来，研究人员一直追求的减少疲劳试验时间的目的。

3.4 用η求疲劳试验时间降低的百分率f

1) 用η求减少的疲劳试验寿命ΔL

ΔL=L50-L′=ηL′-L′=L′(η-1)

(3)

2) 用η求疲劳试验时间降低的百分率f

由于在全尺寸疲劳试验中，完成一个谱块的试验就有一个谱块的寿命，即试验寿命与试验谱块成正比，而每个谱块试验时间又是一定的，因此试验寿命与谱块试验时间成正比，令ΔL对应的时间为Δt，L50对应的时间为t,因此可得

f=Δt/t50=ΔL/L50=L′(η-1)/L′η=1-1/η

(4)

4 试验验证

4.1 30CrMnSiA钢件

1) 疲劳试验件

按中航工业北京航空材料研究院试样标准图纸制作30CrMnSiA钢板试样：中心孔直径∅3,应力集中系数Kt=2.5，890 ℃油淬，520 ℃回火，强度极限δb=1 057 MPa。

2) 试验载荷谱

试验载荷谱由文献[8]中表3和表4提供，谱的基础数据是某机型飞机的实测数据，按谱的损伤值不同编制出：50%损伤的平均谱和58.33%、75%、91.6%损伤的3种重谱。

3) 试验机与试验单位

疲劳试验机是MTSS8810：静载精度≤±1%、动载精度≤2%。

试验单位：中航工业哈尔滨飞机工业集团理化试验室。

4) 疲劳试验、数据和曲线

用50%、58.33%、75%和91.5% 4种损伤谱分别进行疲劳试验，试验数据和计算的η值见表1，根据试验数据和计算的寿命系数η值，绘制的D-L曲线、η-L曲线和η-D曲线如图3所示。

表1 30CrMnSiA钢在不同损伤谱下的试验寿命和寿命系数

Table 1 30CrMnSiA steel test life and life factor at distinct damage spectrum

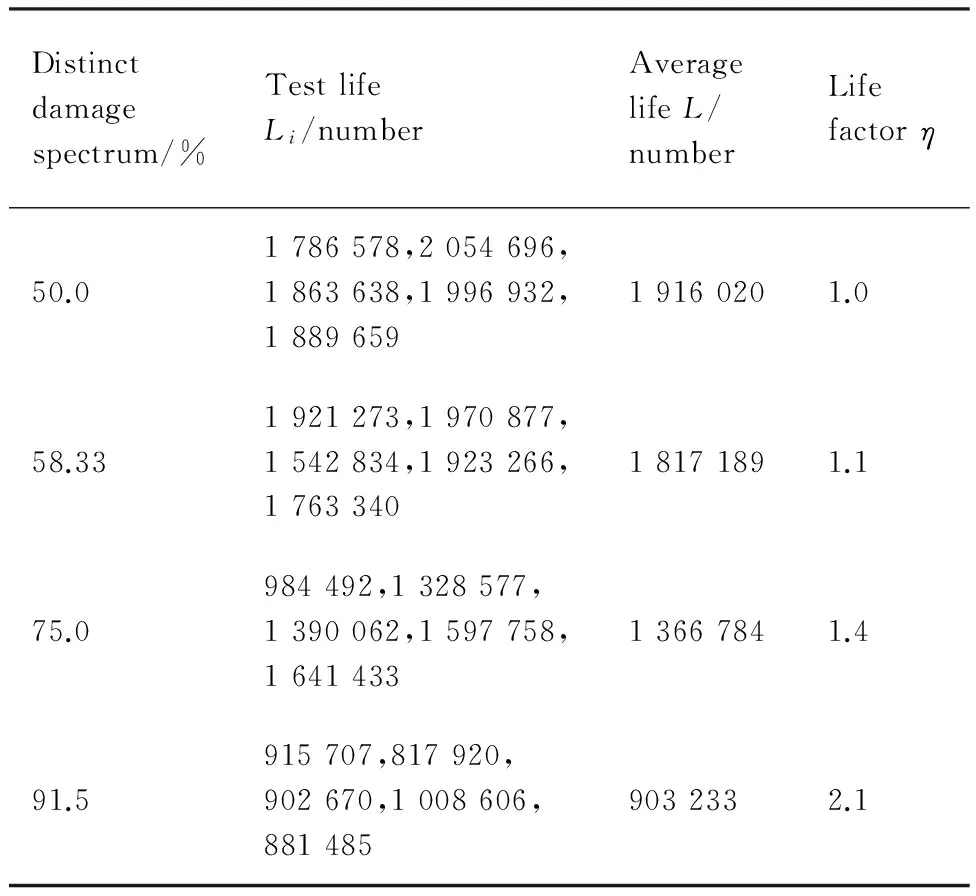
Distinctdamagespectrum/%TestlifeLi/numberAveragelifeL/numberLifefactorη50.01786578,2054696,1863638,1996932,188965919160201.058.331921273,1970877,1542834,1923266,176334018171891.175.0984492,1328577,1390062,1597758,164143313667841.491.5915707,817920,902670,1008606,8814859032332.1

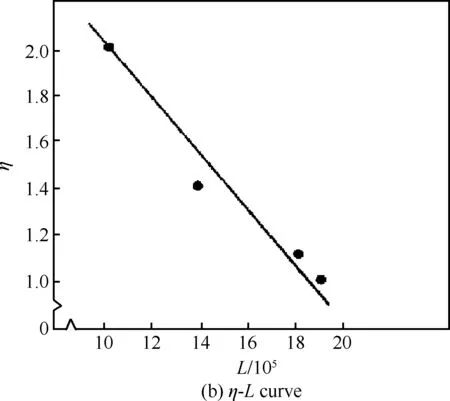
图3 30CrMnSiA试验的D-L,η-L和η -D曲线

Fig.3 D-L， η-L and η -D curves of 30CrMnSiA test

4.2 LC4铝件

为了验证LC4铝件试验的D-L曲线、η-D曲线和η-L的曲线分布规律，从文献[3]的表3～表5 和表3～表6中选出Lc4材料的试验数据，即平均谱(50%损伤值)和3级重谱(58.33%、75%、91.5%损伤值)的疲劳试验寿命Li，列入表2 中，由表2数据和计算值绘制的D-L曲线、η-D曲线和η-L曲线如图4所示。

表2 LC4铝在不同损伤谱下的试验寿命和寿命系数

Table 2 LC4 aluminum test life and life factor at distinct damage spectrum

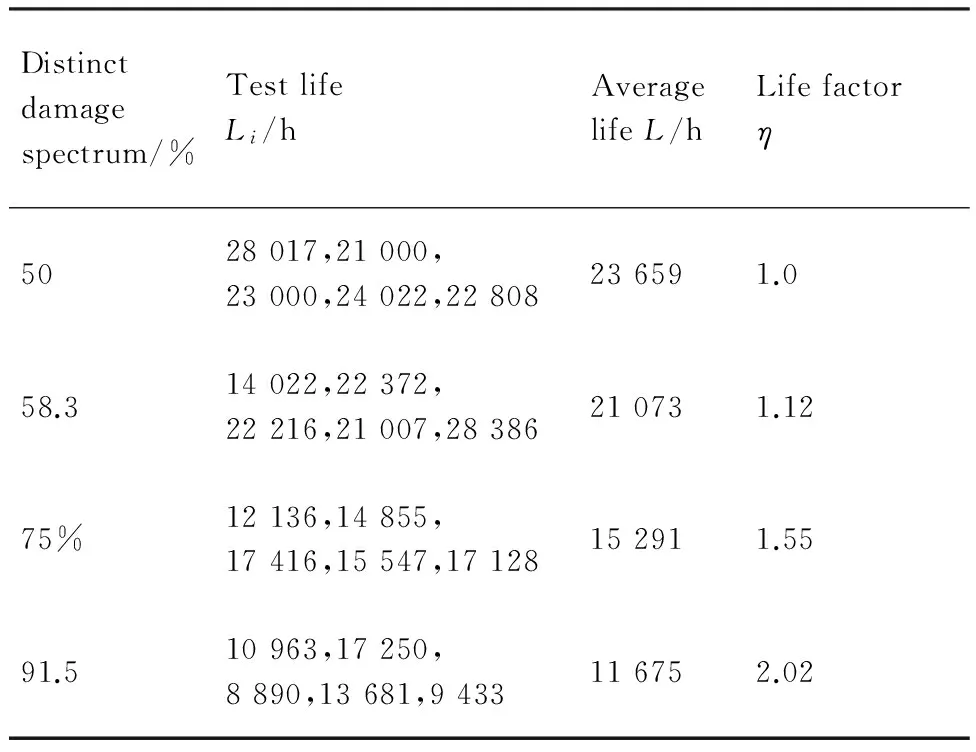
Distinctdamagespectrum/%TestlifeLi/hAveragelifeL/hLifefactorη5028017,21000,23000,24022,22808236591.058.314022,22372,22216,21007,28386210731.1275%12136,14855,17416,15547,17128152911.5591.510963,17250,8890,13681,9433116752.02

4.3 D -L、η -L和η -D曲线分析

1) 钢和铝两种材料试件的试验寿命L(N)与谱的损伤值呈线性关系，与本文论证结论一致。

2) 钢和铝两种材料试件的试验寿命L(N)与寿命系数η呈线性关系，与本文论证结论一致。

3) 钢和铝两种材料试件的试验寿命系数η与谱的损伤值呈线性关系，与本文论证结论一致。

4) 本文的η-D曲线的η=2点对应90%的重谱，这可解释《JSSG—2006》规范规定的重谱可缩减2倍疲劳试验时间。反之，也证明本文的寿命系数定寿法正确。这说明，有了D-L和η-D曲线，人们可以根据试验需要，选择不同重谱进行试验，就可获得相应的缩短试验时间。

5) 图3(c)和图4(c)的η-D曲线还存在延长线的情况，即谱的损伤值小于50%的轻谱情况。由于此情况不仅不能减少全尺寸大部件疲劳试验时间，反而会增加，因此本文没有进行试验验证研究。但此情况对修正轻谱试验寿命是有用的。

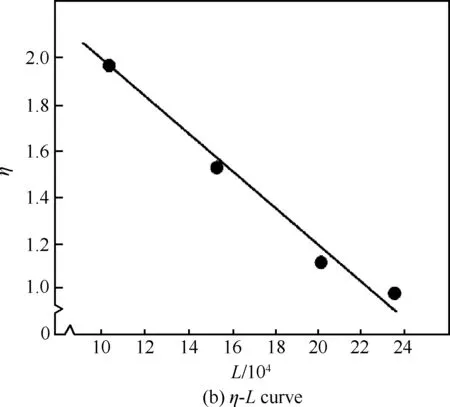
图4 LC4试验的D -L，η -L和η -D曲线

Fig.4 D -L，η -L and η -D curves of LC4 test

5 实施步骤和示例

5.1 编制试验载荷谱

如何编制重谱，目前国内外尚没有公认的方法。文献[9]首次提出按疲劳损伤和载荷加载顺序概念编制“代表起落谱”，之后得到广泛应用。本文认为，编谱要遵循两项基本原则：一要遵循谱的轻重由疲劳损伤大小值控制；二要遵循载荷迟滞效应对寿命影响的规律，即遵循谱的载荷加载顺序对寿命影响规律。本文用于验证试验的平均谱和重谱就是按这两项原则编制的。

1) 平均谱 损伤值是50%的载荷谱。

2) 重谱 损伤值大于50%的载荷谱，如60%、80%、90%损伤谱。

5.2 通过试样疲劳试验绘制η -L曲线

1) 分别用50%、60%、80%和90%损伤谱进行样件疲劳试验，获得各级谱下的寿命L50、L60、L80和L90。

2) 根据η的定义可得：η50=L50/L50=1；η60=L50/L60;η80=L50/L80;η90=L50/L90。

3) 绘制η-L曲线：由样件试验获得的L50、L60、L80、L90和计算获得的各寿命对应的ηi值(1、η60、η80、η90)，可在η-L坐标系中绘出实测曲线，如图7 所示。

5.3 用η求L50的示例

1) 假设用85%损伤谱的重谱做LC4全尺寸结构件的疲劳试验，获得试验寿命L85。

2) 用重谱(85%损伤谱)寿命L85求全尺寸大构件的平均寿命L50：由图4(c)可查得D85对应的η85是1.82，由此，L50=1.82L85。

5.4 用η求疲劳试验时间下降百分率f

以LC4铝为例,由表2的各η值和式(4)求得各重谱下的f：58.33% 重谱的f=0.11、75%重谱的f=0.35、91.5%重谱的f=0.51，即相对平均谱的试验时间，分别降低的疲劳试验时间比率为11%、35%和51%。

6 结 论

1) 通过金属材料疲劳损伤研究，给出金属试件疲劳试验寿命L与疲劳试验谱的损伤值D呈近似线性关系。这个研究结论为不同损伤谱的寿命之间折算提供了理论支持，以此推导出寿命系数等于平均谱的寿命除以重谱的寿命(η=L50/L′)，为建立寿命系数定寿法提供了前提条件。

2) 依据寿命系数内涵，研究给出寿命系数定寿原理和方法。寿命系数定寿法是用高损伤谱试验的大构件寿命乘以小试件试出的寿命系数，可得平均谱下的大构件平均寿命，再用这个平均寿命除以规范规定的分散系数，给出使用寿命。这样既保证了规范规定的分散系数取值不变，又可降低全尺寸构件疲劳试验时间，这是各国疲劳界多年一直希望解决的难题。

3) 本寿命系数定寿法可用于任何损伤谱的疲劳试验和定寿，具有很好的通用性。《JSSG—2006》规范规定可将试验时间缩短1/2，只是本文的η-D曲线上一个点(η=2点)，这不仅证明规范这种规定的的合理性，反之，也证明了寿命系数定寿法的正确性和通用性。利用η-D曲线可修正设计试验谱不准对使用寿命的影响问题。

4) 在相同谱载下，钢和铝的各级寿命系数基本相等，这说明寿命系数取值主要影响因素是试验谱的损伤值，与材料关系不大。由此得出：多种材料组成的整机可用同一寿命系数定寿。

[1] Jointly apply specification guide of U.S.: JSSG-2006[S]. Beijing: Ministry of National Defense, 2006.

[2] 军用飞机强度规范:GJB67.6A-2008[S]. 北京： 国防技术委员会， 2008. Military airplane structural strength specification: GJB67.6A-2008[S]. Beijing: Defense Technology Commission, 2008 (in Chinese).

[3] 张福泽. 使用载荷下的重谱能降低寿命不能降低疲劳分散系数[J]. 航空学报, 2013, 34(8): 1892-1896. ZHANG F Z. Heavy spectra under operational loads may reduce life, but not fatigue scatter factors[J]. Acta Aeronoutica et Astronautica Sinica, 2013, 34(8): 1892-1896 (in Chinese).

[4] 军用飞机强度规范: GJB67.6-85[S]. 北京: 国防技术委员会, 1986. Military airplane structural strength specification: GJB67.6-85[S]. Beijing: Defense Technology Commission, 1986 (in Chinese).

[5] 高镇同. 飞机疲劳分散系数， BH-B884[R]. 北京： 北京航空学院， 1982. GAO Z T. Fatigue scatter factors of aircraft， BH-B884[R]. Beijing: Beijing University of Aeronautical and Astronautics， 1982 (in Chinese).

[6] 张福泽. 裂纹形成寿命类比计算法[J]. 航空学报, 1982,3(2): 51-60. ZHANG F Z. An analogy method for crack initiation life prediction[J]. Acta Aeronoutica et Astronautica Sinica, 1982, 3(2): 51-60 (in Chinese).

[7] 张福泽. 裂纹扩展寿命类比计算法[J]. 航空学报, 1985, 6(2): 194-200. ZHANG F Z. An analogy method for propagation life prediction[J]. Acta Aeronoutica et Astronautica Sinica, 1985, 6(2): 194-200 (in Chinese).

[8] 刘文珽， 王智. 单机寿命监控技术指南[M]. 北京： 国防工业出版社， 2010. LIU W T, WANG Z. Monitoring techniques guide of aircraft life[M]. Beijing: Chinese National Defense Industry press， 2010 (in Chinese).

[9] 张福泽. 飞机载荷谱编制新方法[J]. 航空学报, 1998, 19(5): 518-524. ZHANG F Z. New method of drawing up aircraft load spectrum[J]. Acta Aeronoutica et Astronautica Sinica, 1998, 19(5): 518-524 (in Chinese).

张福泽 男， 中国工程院院士。主要研究方向： 飞机寿命。

Tel: 010-66713310

E-mail: zhangfuzemail@163.com

Received： 2015-09-30； Revised： 2015-10-29； Accepted： 2015-12-06； Published online： 2015-12-22 15:00

URL： www.cnki.net/kcms/detail/11.1929.V.20151222.1500.008.html

*Corresponding author. Tel.： 010-66713310 E-mail: zhangfuzemail@163.com

Theory and method of determination life by life factor

ZHANG Fuze*

AeronauticalArmamentsResearchInstitude,EquipmentAcademyofAirForce,Beijing100076,China

This paper, through research on damage value of fatigue load spectrum, finds out that the fatigue life of metallic material is linear with the damage value of fatigue test load spectrum, namely, the fatigue life of metallic material is linear with the weight of fatigue test load spectrum. Life factor can be deduced from the regularities, and the fatigue test time of full-scale component can be reduced from life factor. From what is displayed in the life factor of existing fatigue test data research, when adding damage value on the basis of average spectrum (fatigue damage value is 50%), 58.3% damage spectrum can reduce 11% of the full-scale component fatigue test time, 75% damage spectrum can reduce 36% and 91.5% damage spectrum can reduce 50%. It comes to the conclusion in this paper as follows: for the purpose of reducing full-scale fatigue test time, load spectrum enhancement is to be employed in full-scale fatigue test, which renders the life in load spectrum enhancement. Then the life factor of sample is used to revert it to the average life under average load spectrum. This average life is then divided by the standard fatigue dispersion coefficient, which renders service life. This method reduces the fatigue test time without violating the standard fatigue dispersion values, making the determination of aircraft life economical and reliable.

fatigue life; fatigue damage; life factor; average spectrum; heavy spectrum

2015-09-30；退修日期：2015-10-29；录用日期：2015-12-06； < class="emphasis_bold">网络出版时间：

时间： 2015-12-22 15:00

www.cnki.net/kcms/detail/11.1929.V.20151222.1500.008.html

.Tel.： 010-66713310 E-mail: zhangfuzemail@sina.com

张福泽． 寿命系数定寿的原理和方法[J]． 航空学报, 2016, 37(2): 404-410. ZHANG F Z. Theory and method of determination life by life factor[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(2): 404-410.

http://hkxb.buaa.edu.cn hkxb@buaa.edu.cn

10.7527/S1000-6893.2015.0330

V215.5

：A

： 1000-6893(2016)02-0404-07

*