后掠机翼人工转捩最佳粗糙带高度数值预测

田永强， 张正科,*， 屈科， 翟琪

1.西北工业大学 翼型叶栅空气动力学国家重点实验室， 西安 710072 2.纽约城市大学 城市学院 土木工程系， 纽约 NY10031, 美国

后掠机翼人工转捩最佳粗糙带高度数值预测

田永强1， 张正科1,*， 屈科2， 翟琪1

1.西北工业大学 翼型叶栅空气动力学国家重点实验室， 西安 710072 2.纽约城市大学 城市学院 土木工程系， 纽约 NY10031, 美国

介绍了基于当地变量的γ-Reθ转捩模型，并将该模型应用到后掠机翼的转捩预测和人工转捩最佳粗糙带高度以及人工转捩技术能够模拟的大气飞行雷诺数的确定中。为检验γ-Reθ转捩模型对后掠机翼转捩的预测能力，对ONERA M6机翼和DLR-F4标模机翼进行了边界层转捩预测，采用结构化网格和有限体积法求解雷诺平均Navier-Stokes(RANS)方程，得到了机翼表面的摩擦阻力系数分布，从而可以得到相应的转捩位置，预测得到的转捩位置与试验结果比较吻合，说明该模型对后掠机翼转捩预测是可信的。最后在DLR-F4标模机翼上表面固定了粗糙带，通过相同的方法得到了转捩位置，从而确定了马赫数为0.785、雷诺数为3.0×106时最佳粗糙带高度为0.11 mm；通过不断增大雷诺数使自由转捩位置不断向前缘移动，验证了人工转捩对大气飞行雷诺数的模拟能力。结果表明，在最佳粗糙带高度为0.11 mm 下，可以实现对大气飞行高雷诺数的模拟。

人工转捩； 粗糙带高度； 转捩模型； 后掠机翼； 雷诺数； 边界层

飞行器模型风洞试验除非在全尺寸雷诺数风洞中进行，否则模型的边界层状态是不能完全模拟飞行器在大气中的飞行情形的。大气飞行的全尺寸飞行器，从各部件的前缘区域开始多为湍流，如果不采取人工转捩措施，风洞试验模型上总存在相当长度的层流区[1-4]。这种情况在小迎角时主要影响阻力，较大迎角时由于层流和湍流分离情形的不同，也会影响飞行器的其他气动参数，从而使得风洞试验所得数据的工程应用价值大大降低。为了能在小尺寸风洞中获得具有高雷诺数特点的试验数据，通常采用边界层人工转捩的方法，而其中最常用的就是粘贴粗糙带强制模型表面边界层在粗糙带处转捩。

一般来讲，在给定雷诺数下，当粗糙带较低时，转捩会发生在粗糙带下游某处，当粗糙带高度逐渐增加时，转捩位置会从下游向粗糙带逼近，直到某个高度转捩恰好发生在粗糙带所在位置，这个高度就是使转捩发生在粗糙带处的最小高度，当粗糙带高度继续增加超过这个最小高度后，转捩仍然发生在粗糙带处，所以高度增加的部分除了对流场带来更大的扰动、增加额外阻力外，对人工转捩试验并无实际益处。因而这个最小粗糙带高度即最佳粗糙带高度。事实上这个最小粗糙带高度仍然会对流场、压力分布造成扰动，也带来附加阻力，但这是在小尺寸风洞中要模拟大气飞行条件下全尺寸飞行器表面边界层状态的人工转捩试验必须付出的代价。通常对粗糙带的基本要求为：①在粗糙带下游，模型边界层由层流转捩为稳定的湍流；②经过粗糙带后边界层厚度增加较少，对边界层外势流影响小；③粗糙带附加阻力小[3]。为把粗糙带高度对流场、压力分布、阻力造成的影响降低到最小程度，需要确定出最佳粗糙带高度。

确定最佳粗糙带高度归根结底是要准确地判断转捩的发生。层流向湍流的转捩是现代流体力学领域最具挑战性的难题之一。边界层转捩通常可划分为3种模式：自然转捩、旁路转捩和分离诱导的转捩。

自然转捩是指自由来流湍流度小于1%的情形下的转捩[5-6]。其转捩过程包括几个阶段：①当动量厚度雷诺数达到一个临界值时层流边界层变为线性不稳定，并且对微小扰动很敏感，从而发展成一种二维Tollmien-Schlichting波形式的不稳定；②这个不稳定性在边界层内获得某种程度的放大，使得这个不稳定波变为非线性，从而无黏机制发挥作用，导致带有大脉动的三维扰动出现[7]；③三维不稳定模态在基态和零频率下增长，增长过程中展向速度分布形成波峰和波谷，基态在每个周期形成的Λ结构会排成行，每个Λ结构主要包括连续变形的Λ涡和一个三维的Λ或Δ形的强剪切层，剪切层导致Λ结构的连续拉伸与其“腿部”的涡量集中；④三维高频谱模态的快速生长，在Λ涡中间阶段，其腿部尖端多次重联形成发卡涡，发卡涡在流向速度的时间序列中其中央出现瞬时“尖峰”并在下游逐渐增多，近壁面区域峰值位置附近，准随机的非周期性扰动增长[8]；⑤流动中高度脉动的部分发展成为湍斑，湍斑不断增长，并在层流边界层中向下游运动，聚合成充分发展的湍流边界层[5,9]。

旁路转捩是指自由来流湍流度大于1%的情形下的转捩。在这个模式中，由于来流湍流度较高，自然转捩的第一阶段(也可能包括第二、三、四、五阶段)被完全跳过，从而在来流扰动的影响下湍斑直接在边界层内生成。到目前为止还没能在来流湍流度大于1%的情形下在边界层内探测到Tollmien-Schlichting波，因此，1%的来流湍流度经常被看做是自然转捩和旁路转捩的分水岭。应该注意的是，壁面粗糙度也可导致旁路转捩，只不过这里的扰动发源于壁面而非源于来流湍流度。另外，直接给边界层注入湍流也可能导致旁路转捩发生，比如在发热的涡轮叶片或静子上的冷却孔注入湍流[5,9]。

分离诱导的转捩是指层流边界层在压力梯度影响下发生分离，转捩就会因无黏不稳定机制而在分离的剪切层(可能再附也可能不再附)里发展和发生。这种情况下，由于湍流导致的强化掺混，剪切层可能会再附。这种再附会在壁面形成层流分离/湍流再附式气泡。这种类型的转捩会在边界层绊线后出现，并因强逆压梯度引起的分离所致[6,10]。

试验中判断转捩及确定最佳粗糙带高度的方法有升华法[11-14]和温敏漆(Temperature Sensitive Paint, TSP)技术[15-16]。但最佳粗糙带高度一般会随雷诺数变化，雷诺数越大，最佳粗糙带高度越小。如果用试验手段确定某雷诺数下的最佳粗糙带高度，需要反复尝试，成本高、周期长。而用数值模拟的方法预测转捩、人工转捩及最佳粗糙带高度，则可为试验提供先期指导，大大节省试验成本。

预测转捩的数值方法主要有：①基于小扰动理论的线性稳定性理论的eN方法；②求解抛物型稳定性方程(PSE)方法；③直接数值模拟(DNS)方法和大涡模拟(LES)方法；④基于湍流模型的方法。eN方法是基于线性稳定性理论的半经验方法，它假设边界层内各种频率的小扰动向下游传播，当其参数进入中性曲线不稳定区域后，它们就会被放大。各频率的波从开始被放大处起，设沿波的传播方向累计的线性放大倍数达到预设值eN时的位置为xT(ω)，那么各频率求得的最小xT就是转捩发生的位置[17-18]。eN方法既没有考虑初始扰动性质及大小，也没有考虑非线性演化的影响，所以N只能是一种经验值，而且只能适用于边界层外的流动扰动很小的情况，对每一类情况都需要确定相应的N的取值[19-21]。PSE方法用PSE计算初始扰动的演化，一旦演化变得剧烈，表现为计算发散，或扰动动能和摩擦力系数剧烈抬升，则认为突变过程开始，转捩发生，PSE方法虽然取得了很大的进步，但还处于发展过程中[22-24]。DNS方法和LES方法计算量大，对计算机硬件要求较高，目前距离工程应用还有很大距离[25-26]。基于雷诺平均方程的湍流模型预测方法利用湍流模型来预测转捩，抓住了转捩的统计特性。这方面的研究可分为3类：低雷诺数湍流模型及其修正形式、考虑间歇性的转捩模型和最近出现的基于当地变量的新型模型。由当地变量构造的新型模型中最具代表性的是Menter和Lantry在2004年提出的一种耦合到剪切应力输运(SST)k-ω二方程模型中的完全基于流场当地变量的γ-Reθ转捩模型[5,9,17-19]。γ-Reθ转捩模型考虑了间歇因子γ和动量厚度雷诺数Reθ，构造了两个变量的输运方程，和原SSTk-ω二方程模型结合起来，又称为Transition SST四方程模型。该模型的特点[19]是：①可以使用不同的经验函数进行标定；②能够涵盖不同的转捩机制；③不依赖于初场，即无论初始边界层是层流还是湍流都具有相同的解；④不影响基础湍流模型在完全湍流区的行为；⑤不依赖坐标系的选取；⑥适用于三维边界层的流动。成婷婷等[17-18]采用γ-Reθ转捩模型对翼型风洞固定转捩试验最佳粗糙带高度进行了数值预测，表明该转捩模型对翼型转捩位置和最佳粗糙带高度具有很好的预测能力。

本文用γ-Reθ转捩模型对后掠机翼的自由转捩进行数值模拟预测，验证模型对后掠机翼转捩的模拟能力，并在此基础上对后掠机翼人工转捩的最佳粗糙带高度进行数值预测。

1 γ -Reθ转捩模型简介

1.1 间歇因子输运方程

模拟转捩区流动需要引入间歇因子γ，γ-Reθ转捩模型中γ定义为流动处于有脉动和无脉动状态的时间比例，控制着湍斑的生成，当转捩开始后γ开始增长，湍流涡黏性系数μt被重新定义为μt,eff=γμt。间歇因子γ输运方程为

(1)

式中：σγ=1；ρ为密度；U为当地速度；t为时间尺度；μ为黏性系数；转捩源项为

(2)

式中：S为应变率的模；Flength为控制转捩区长度的经验关联函数；Fonset为触发间歇因子γ增长的函数；Ca1=2；Ce1=1；Cγ3=0.05。再层流化源项为

(3)

式中：Ω为涡量的模；Ca2=0.06；Ce2=50；Fturb定义为

(4)其作用为使层流边界层或者黏性底层外的再层流化源项失去作用。转捩触发由式(5)～式(10)控制。

(5)

(6)

(7)

(8)

Fonset3=max(0,1-(RT/2.5)3)

(9)

Fonset=max(0,Fonset2-Fonset3)

(10)

1.2 转捩动量雷诺数的输运方程

转捩动量厚度雷诺数的输运方程为

(11)

其中源项定义为

式中：cθt=0.03；σθt=2.0；Fθt定义为

转捩所使用的经验关系式为

F(λθ)=

式中：Tu为边界层外自由来流的湍流强度；λθ为流向压力梯度参数，定义为

1.3 转捩模型与湍流模型的结合

耦合了转捩模型后的SSTk -ω二方程湍流模型控制方程为

F1=max(F1orig,F3)

式中：Pk、Dk和F1orig为SST湍流模型的生成项、破坏项和混合函数；F1为修正的混合函数，具体含义参见文献[5]。

2 计算方法与转捩判据

采用有限体积法和结构网格求解雷诺平均Navier-Stokes(RANS)方程，湍流模型采用二方程SST湍流模型与γ-Reθ转捩模型耦合得到的Transition SST模型，选用基于密度的隐式算法，时间推进采用二阶迎风格式。

一般来讲，在壁面附近，层流边界层的速度型比较尖瘦，湍流边界层速度型比较饱满，因而层流边界层近壁处的速度梯度小于湍流边界层。从而导致层流边界层摩擦力系数小于湍流边界层摩擦力系数，即(Cf)lam<(Cf)turb，那么在转捩发生的位置，一定会出现表面摩擦力系数的突然增大。这可以作为判断转捩的依据。

3 γ -Reθ模型对后掠翼自由转捩的预测

3.1 ONERA M6机翼自由转捩预测

ONERA M6机翼[27-28]是一个后掠梯形翼，展弦比为3.8，尖削比为0.562，前缘后掠角为30°，后缘后掠角为15.8°，1/4弦线后掠角为26.7°。本文生成了3套C-H型多块对接结构网格用于研究网格敏感性。为了模拟边界层转捩，3套网格近壁面第一层网格间距均取3×10-6m，以满足y+≈1，壁面附近网格的法向伸展率均为1.30。Grid 01在物面法向的网格点数为48，上下翼面流向网格点数均为85，后缘割缝流向网格点数上下均为40，机翼展向网格点数为32，总网格点数为1 033 280，如图1所示。Grid 02为Grid 01沿物面法向加密1.5倍所得到的网格，Grid 03为Grid 02沿物面流向加密1.5倍所得到的网格。Grid 02和Grid 03的网格点数分别为1 311 600和1 592 020。

图1 ONERA M6机翼C-H网格

Fig.1 C-H grid for ONERA M6 wing

图2分别给出了3套网格采用γ-Reθ转捩模型计算来流马赫数Ma∞=0.839 5、雷诺数Re∞=11.72×106、迎角α=3.06°条件下ONERA M6机翼η=20%，44%，65%，80%，90%，95%和99%展向站位的弦向压力系数Cp分布，由图可见3套网格计算结果差异很小，且均与实验结果[29]吻合良好，表明计算所采用的网格和算法是可行的。

图3是来流湍流度Tu≈ 0.2%、马赫数Ma∞=0.262、雷诺数Re∞=3.5×106、迎角α=0°, 5°，15°条件下风洞试验萘升华法测量的转捩位置结果[27-28]，其中白色区域为层流区。

图2 ONERA M6机翼表面压力系数分布计算与实验比较

Fig.2 Comparison of pressure coefficient distribution on ONERA M6 wing surface between computed and experimental results

图3 ONERA M6机翼升华法转捩试验结果[27-28]

Fig.3 Transition test results on ONERA M6 wing with sublimation method[27-28]

用γ-Reθ转捩模型在3套网格上计算转捩，设置来流间歇因子γ=0.42，湍流度Tu=3%，湍流黏性比μt/μ=40；取马赫数Ma∞=0.262，Re∞=3.5×106[27]。图4给出了3套网格计算得出的机翼表面摩擦力系数Cf的分布云图。可以看出，除了迎角为15°的上表面外，3套网格计算的转捩位置均与实验结果比较接近，并且3套网格计算的翼面Cf云图差别较小，说明计算结果对3个网格不敏感，也说明用Grid 01网格计算是可信的。这个结果表明γ-Reθ转捩模型用于后掠机翼的转捩预测是可行的。

图5给出了α=0°, 5°, 15°时采用Grid 01计算ONERA M6机翼得到的上翼面流线图，由图可知，当迎角为0°和5°时，机翼表面沿展向的横向流动不明显，主要表现为二维流动特征，而当迎角为15°时，机翼上表面出现的分离导致流动具有较明显的横流特征，而γ-Reθ转捩模型本身对于横流不稳定性导致的转捩不具备可靠的预测能力[28]，所以在α=15°时预测的转捩位置与实验偏差较大。

3.2 DLR-F4标模机翼自由转捩预测

DLR-F4标模机翼为典型的跨声速标准模型[30]。本文计算只取其机翼作为计算模型，该机翼前缘后掠角为27.1°，后缘后掠角为18.9°，1/4弦线后掠角为25°，展弦比为9.5。为研究网格敏感性，生成了3套O-H/C-H型多块对接结构网格，内块为O-H型，外块为C-H型。为模拟边界层转捩，3套网格近壁面第一层网格间距均取1×10-6m，以满足y+≈1的要求，壁面附近网格法向伸展率均为1.30。Grid 01的内块O-block网格径向网格点数为20，上下翼面流向网格点数均为59，机翼展向网格点数为70，外块网格径向网格点数为20。Grid 01网格点数为518 226，如图6 所示。Grid 02为Grid 01在O-block内块沿机翼表面法向加密1.5倍所得到的网格，Grid 03为Grid 02网格沿翼面流向加密1.5倍所得到的网格。Grid 02和 Grid 03的网格点数分别为638 518 和819 414。

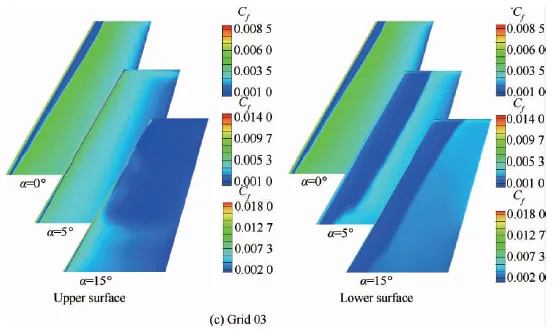
图4 ONERA M6机翼表面摩擦力系数云图

Fig.4 Friction coefficient contours on ONERA M6 wing surface

图5 ONERA M6机翼上表面流线

Fig.5 Streamlines on upper surface of ONERA M6 wing

图6 DLR-F4标模机翼的计算网格

Fig.6 Computational mesh of DLR-F4 standard model wing

图7为ETW(European Transonic Wind Tunnel)采用温敏漆技术测量的马赫数Ma∞=0.785、雷诺数Re∞=6×106下的DLR-F4标模机翼表面自由转捩结果[31]。

用γ-Reθ转捩模型在3套网格上计算转捩。设置来流间歇因子γ=0、湍流度Tu=0.125%、湍流黏性比μt/μ=10，取Ma∞=0.785、Re∞=6×106。图8给出了3套网格计算的机翼表面的摩擦力系数云图。可以看出，3套网格预测的转捩位置均在实验结果之前，只能大致与实验结果相对比。其中，Grid 03在α=-0.87°, -1.58° 下比Grid 01、Grid 02的转捩位置略靠后，更靠近实验结果一些。整体上3套网格计算结果差别很小，说明计算结果对3套网格不敏感，也就是说用Grid 01计算是可行的。该机翼的计算结果说明用γ-Reθ转捩模型可以大致预测较大展弦比后掠机翼的转捩。

图7 ETW DLR-F4标模机翼温敏漆转捩试验结果

(Ma∞=0.785, Re∞=6×106)[31]

Fig.7 TSP tests results of transition on DLR-F4 standard model wing at ETW (Ma∞=0.785, Re∞=6×106)[31]

图8 DLR-F4标模机翼上表面摩擦力系数云图(Ma∞=0.785, Re∞=6×106)

Fig.8 Friction coefficient contours on DLR-F4 standard model wing upper surface (Ma∞=0.785, Re∞=6×106)

图9给出了Grid 01计算所得的DLR-F4标模机翼上表面流线图，流线呈明显的二维特征，所以可以用γ-Reθ模型预测其转捩。

图9 DLR-F4标模机翼上表面流线

Fig.9 Streamlines on upper surface of DRL-F4 standard model wing

通过对ONERA M6机翼和DLR-F4标模机翼的自由转捩数值预测可知，对展弦比较小的后掠翼，γ-Reθ模型对小迎角情形的转捩预测比较可信，对α≥15°的较大迎角情形，如果翼面出现比较明显的横向流动，γ-Reθ模型预测的转捩不准确或可能预测不到转捩；对展弦比较大的后掠翼，γ-Reθ模型能预测出大致的转捩位置。

4 最佳粗糙带高度预测

以DLR-F4标模机翼安装在一个试验段截面尺寸为800 mm(宽)×600 mm(高)的跨声速风洞进行半模试验为例，按照堵塞度的限制要求，半模展长一般不超过试验段宽度的0.6倍[1-2]，将机翼模型展长限制在480 mm。根据粗糙带的粘贴要求[4]，沿DLR-F4标模机翼模型上表面7%弦长线上构造粗糙带几何模型，粗糙带宽度为当地弦长的1.5%，高度沿展向不变，横截面呈矩形。计算采用C-H型多块对接结构网格，上下翼面流向网格点数均为59，尾迹区网格点数为40，物面法向网格点数为48，机翼展向网格点数为60，其中粗糙带表面流向为5个网格点，侧面高度方向为9个网格点，整个网格总网格点数为636 397。为了模拟边界层转捩，近壁面第一层网格间距取为 1.4×10-6m，以满足y+≈1的要求，网格伸展率为1.30，如图10所示。

选取计算来流条件为马赫数Ma∞=0.785、雷诺数Re∞=3×106、迎角α=-4.85°。设置来流间歇因子γ=0，湍流度Tu=0.125%，湍流黏性比μt/μ=10。

图10 DLR-F4标模机翼粗糙带附近的网格

Fig.10 Grid near roughness strip on DLR-F4 standard model wing

图11给出了马赫数Ma∞=0.785、Re∞=3×106、α=-4.85°，粗糙带高度h分别为0.09、0.10、0.11、0.12 mm时机翼表面摩擦力系数云图及25%、50%和75%展向站位弦向摩擦力系数分布。由图可见，当粗糙带高度为0.09 mm和0.10 mm 时，粗糙带下游还有一部分层流区域，而当粗糙带高度增长到0.11 mm和0.12 mm时，粗糙带下游全为湍流。故知Ma∞=0.785、Re∞=3.0× 106、α=-4.85°时最佳粗糙带高度为0.11 mm。

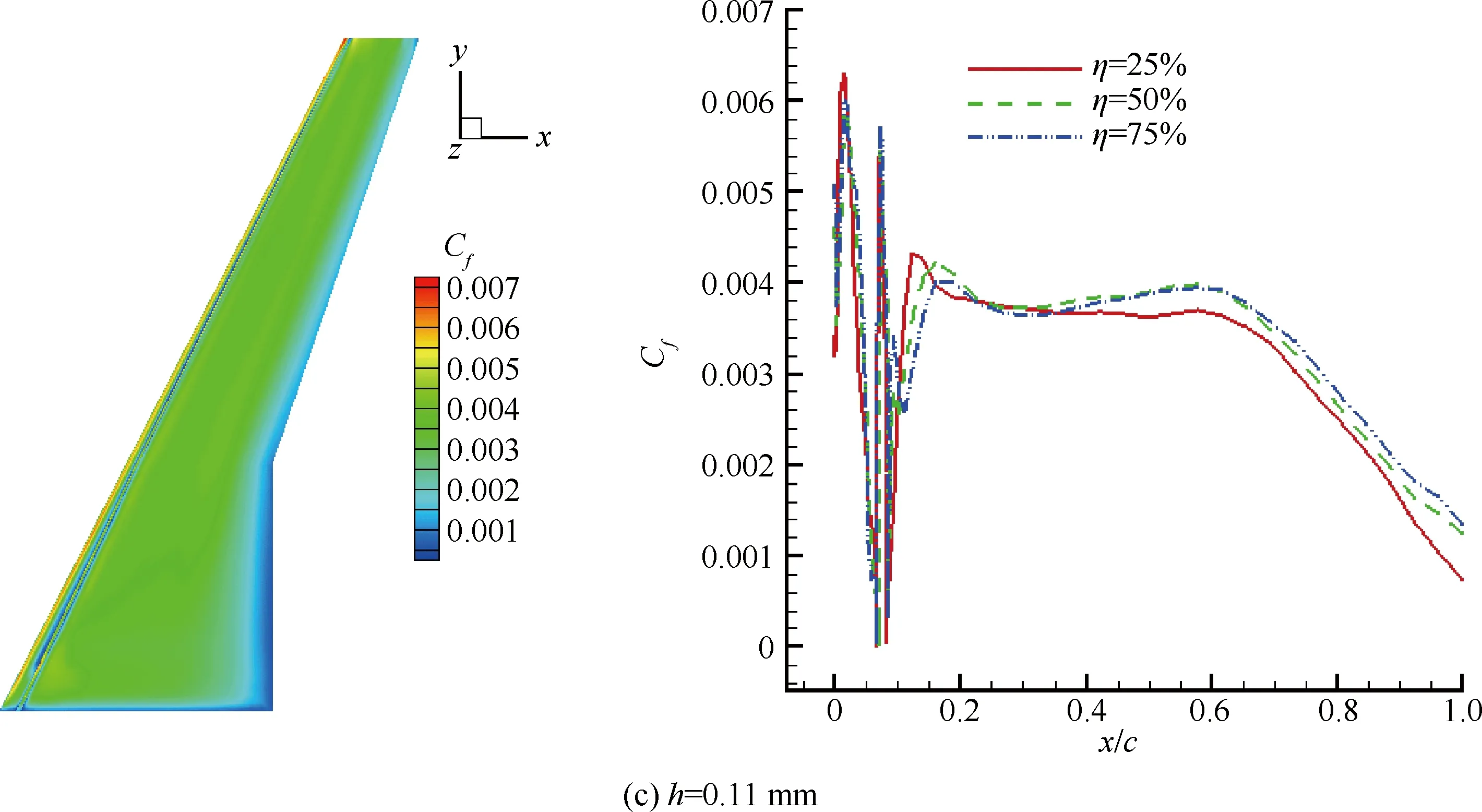
图11 DLR-F4标模机翼上表面摩擦力系数分布

Fig.11 Friction coefficient distribution on upper surface of DLR-F4 standard model wing

为了解最佳粗糙带高度与边界层厚度之间的关系，选取与计算最佳粗糙带高度相同的来流条件为Ma∞=0.785、Re∞=3×106、α=-4.85°，计算光洁表面DLR-F4标模机翼流场，获得其边界层厚度从翼根到翼稍逐渐减小的结果。图12给出了机翼上表面10%(翼根附近)和98%(翼稍附近)两个展向站位处7%c(c为当地弦长)的速度型，由图可见，翼根附近边界层厚度约为0.185 mm，翼稍附近边界层厚度约为0.125 mm，均大于最佳粗糙带高度，可知粗糙带没有伸出边界层。

图12 DLR-F4标模机翼不同展向站位7%弦长点处上翼面速度型

Fig.12 Velocity profile on upper surface of DLR-F4 standard model wing at 7% chordwise point of different spanwise stations

为了判断低雷诺数Re∞=3.0×106下的人工转捩对全尺寸高雷诺数机翼表面边界层的模拟程度，不断增大雷诺数计算光洁表面DLR-F4标模机翼的自由转捩，获得其转捩位置与人工转捩位置7%c相同时的雷诺数。在Ma∞=0.785、α=-4.85°时，计算获得Re∞=13.97×106下，其转捩位置在展向不呈一条直线，而是在机翼内区已达到前缘，在外区则在14%c附近(参见图13)，可以认为其平均转捩位置为7%c。故可知在Ma∞=0.785、Re∞=3×106、α=-4.85°下的人工转捩模拟的就是Re∞=13.97×106飞行条件下的自由转捩。

图13 飞行雷诺数Re∞=13.97×106下DLR-F4标模机翼上表面自由转捩摩擦力系数云图

图14给出了Re∞=3×106、人工转捩最佳粗糙带下机翼25%、50%、75%这3个展向站位的压力系数分布与大气飞行雷诺数Re∞=13.97×106下光洁机翼表面压力系数分布的比较。可以看出，除了在粗糙带附近压力有跳动及在后缘略有偏差外，人工转捩获得的压力分布与大气飞行状态吻合较好。这样，可将低雷诺数人工转捩试验时粗糙带处的压力跳动进行光顺，即可模拟大气飞行高雷诺数下的压力分布，从而能较准确地模拟升力系数和力矩系数。另外，人工转捩得到的阻力系数为CD= 0.011 729 6，大雷诺数光洁机翼的阻力系数为CD=0.012 417 034，二者相差0.000 688，而高速风洞在跨声速段对阻力测量精度要求的合格指标为0.000 50,先进指标为0.000 10，所以工人转捩造成的阻力误差其实接近测量误差。

图14 DLR-F4标模机翼粗糙带人工转捩与飞行雷诺数下自由转捩翼剖面压力系数分布比较

Fig.14 Comparison of chordwise pressure distributions between DLR-F4 standard model wing roughness strip artificial transition and atmospheric flight free transition

5 结 论

1) 对展弦比较小的后掠翼，γ-Reθ模型对小迎角情形的转捩预测比较可信，对α≥15°的较大迎角情形，如果翼面出现比较明显的横向流动，γ-Reθ模型预测的转捩不准或可能预测不到转捩；对展弦比较大的后掠翼，γ-Reθ模型能预测出大致的转捩位置。

2) 对于DLR-F4机翼，在马赫数为0.785，雷诺数为3×106时，γ-Reθ模型预测的最佳粗糙带高度为0.11 mm，该高度下的人工转捩可近似模拟相同马赫数下雷诺数约为13.97×106的大气飞行自由转捩结果。

3) 机翼人工转捩试验能模拟飞行雷诺数条件下的边界层状态、压力分布、升力系数、力矩系数，基本可以获得具有高雷诺数特点的试验结果。

[1] 范洁川. 风洞试验手册[M]. 北京：航空工业出版社， 2002： 313-314. FAN J C. Wind tunnel experiment handbook[M]. Beijing: Aviation Industry Press, 2002: 313-314 (in Chinese).

[2] 恽起麟. 实验空气动力学[M]. 北京： 国防工业出版社， 1991： 13-15. YUN Q L. Experimental aerodynamics[M]. Beijing: National Defense Industrial Press, 1991: 13-15 (in Chinese).

[3] 恽起麟. 风洞实验数据的误差与修正[M]. 北京： 国防工业出版社， 1996: 276-277. YUN Q L. Wind tunnel experiment data errors and correction[M]. Beijing: National Defense Industrial Press, 1996: 276-277 (in Chinese).

[4] 程厚梅. 风洞实验干扰与修正[M]. 北京： 国防工业出版社， 2003： 292-299. CHENG H M. Wind tunnel experiment interference and correction[M]. Beijing: National Defense Industrial Press, 2003: 292-299 (in Chinese).

[5] LANGTRY R B. A correlation-based transition model using local variables for unstructured parallelized CFD codes[D]. Stuttgart: Stuttgart University, 2006.

[6] MAYLE R E. The role of laminar-turbulent transition in gas turbine engines[J]. ASME Journal of Turbomachinery, 1991, 113(4): 509-537.

[7] KLEBANOFF P S, TIDSTROM K D, SARGENT L M. The three-dimensional nature of boundary layer instability[J]. Journal of Fluid Mechanics, 1962, 12(1): 1-24.

[8] LEE C B, WU J C. Transition in wall-bonded flows[J]. Applied Mechanics Reviews, 2008, 61(030802): 1-21.

[9] LANGTRY R B, MENTER F R. Correlation-based transition modeling for unstructured parallelized computational fluid dynamics codes[J]. AIAA Journal, 2009, 47(12): 2894-2906.

[10] MALKIEL E, MAYLE R E. Transition in a separation bubble[J]. Journal of Turbomachinery, 1996, 118(4): 752-759.

[11] 杨永， 左岁寒， 李喜乐， 等. 基于升华法实验研究后掠翼三维边界层的转捩[J]. 实验流体力学， 2009， 23(3)： 40-43. YANG Y, ZUO S H, LI X L, et al. Transition studies for the boundary layer on a swept wing based on sublimation technique[J]. Journal of Experiments in Fluid Mechanics, 2009, 23(3): 40-43 (in Chinese).

[12] 黄勇， 钱丰学， 于昆龙, 等. 基于柱状粗糙元的边界层人工转捩试验研究[J]. 实验流体力学， 2006， 20(3)： 59-62. HUANG Y, QIAN F X, YU K L, et al. Experimental investigation on boundary layer artificial transition based on transition trip disk[J]. Journal of Experiments in Fluid Mechanics, 2006, 20(3): 59-62 (in Chinese).

[13] 任旭东， 赵子杰， 高超， 等. 一种新型转捩技术在跨音速风洞中的应用[J]. 实验力学， 2013， 28(3)： 314-319. REN X D, ZHAO Z J, GAO C, et al. Application of a new transition technology in transition wind tunnel[J]. Journal of Experimental Mechanics, 2013, 28(3): 314-319 (in Chinese).

[14] 赵子杰， 高超， 张正科. 新型人工转捩技术研究及试验验证[J]. 航空学报， 2015， 36(6)： 1830-1838. ZHAO Z J, GAO C, ZHANG Z K. Study of an innovative transition technique and its validation through wind tunnel experiments[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(6): 1830-1838 (in Chinese).

[15] FEY U, EGAMI Y, ENGLER R H. High Reynolds number transition detection by means of temperature sensitive paint: AIAA-2006-0514[R]. Reston: AIAA, 2006.

[16] YORITA D, ASAI K, KLEIN C, et al. Transition detection on rotating propeller blades by means of temperature-sensitive paint: AIAA-2012-1187[R]. Reston: AIAA, 2012.

[17] CHENG T T, ZHANG Z K, QU K, et al. Numerical study of fixed artificial transition and the minimum height of roughness strip for it: AIAA-2013-3093[R]. Reston: AIAA, 2013.

[18] 成婷婷， 张正科， 屈科. 用转捩模型预测转捩及确定最佳粗糙带高度[J]. 航空计算技术， 2012， 42(5)： 75-79. CHENG T T, ZHANG Z K, QU K. Prediction of transition and optimal roughness height based on transition model[J]. Aeronautical Computing Technique, 2012, 42(5): 75-79 (in Chinese).

[19] 张玉伦， 王光学， 孟德虹, 等.γ-Reθ转捩模型的标定研究[J]. 空气动力学学报， 2011， 29(3)： 295-301. ZHANG Y L, WANG G X, MENG D H, et al. Calibration ofγ-Reθtransition model[J]. Acta Aerodynamica Sinica, 2011, 29(3): 295-301 (in Chinese).

[20] STOCK H W, HAASE W. Navier-Stokes airfoil computation with eNtransition prediction including transitional flow regions[J]. AIAA Journal, 2000, 38(11): 2059-2066.

[21] ZHOU H, ZHAO G F. Flow stability[M]. Beijing: National Defense Industrial Press, 2004: 65-67 (in Chinese). 周恒， 赵耕夫. 流动稳定性[M]. 北京： 国防工业出版社， 2004： 65-67.

[22] HERBERT T. Parabolized stability equations[J]. Annual Review of Fluid Mechanics, 1997, 29(1): 245-283.

[23] MALIK M R, LI F. Transition studies for swept wing using PSE: AIAA-1993-0077[R]. Reston: AIAA, 1993.

[24] HAYNES T S, READ H L, SARIC W S. CFD validation issues in transition modeling: AIAA-1996-2051[R]. Reston: AIAA, 1996.

[25] LIU Z, ZHAO W, LIU C, et al. Direct numerical simulation of flow transition in high-speed boundary layers around airfoils: AIAA-1997-0753[R]. Reston: AIAA, 1997.

[26] FASEL H F, MEITZ H L, BACHMAN C R. DNS and LES for investigating transition and transtion control: AIAA-1997-1820[R]. Reston: AIAA, 1997.

[27] ANDREAS K. Automatic transition prediction and application to 3D wing configurations: AIAA-2006-0914[R]. Reston: AIAA, 2006.

[28] CORNELIA G， ANDREAS K. Correlation-based transition transport modeling for three-dimensitional aerodynamic configurations[J]. Journal of Aircraft, 2013, 50(5): 1533-1539.

[29] NASA. NPARC alliance validation archive[EB/OL]. [2014-12-17]. http://www.grc.nasa.gov/WWW/wind/ valid/m6wing/m6wing.html.

[30] VASSBERG J C, BUNING P G, RUMSEY C L. Drag prediction for DLR-F4 wing/body using OVERFLOW and CFL3D on overset mesh: AIAA-2002-0840[R]. Reston: AIAA, 2002.

[31] FEY U, EGAMI Y, JANSEN U, et al. Transition detection by temperature sensitive paint at cryogenic temperatures in the European transonic wind tunnel (ETW)[C]//20th International Congress on Instrumentation in Aerospace Simulation Facilities, ICIASF 2003. 2003: 77-88.

田永强 男， 硕士研究生。主要研究方向： 计算流体力学。

E-mail: nwpuqiangge@mail.nwpu.edu.cn

张正科 男， 博士， 教授， 硕士生导师。主要研究方向： 计算流体力学。

Tel: 029-88491224-15

E-mail: zkzhang@nwpu.edu.cn

屈科 男， 博士研究生。主要研究方向： 计算流体力学， 计算海洋动力学。

E-mail: kequ00@citymail.cuny.edu

翟琪 男， 硕士研究生。主要研究方向： 计算流体力学， 流动控制。

E-mail: zhaiqi@mail.nwpu.edu.cn

Received： 2015-03-03； Revised： 2015-03-17； Accepted： 2015-05-08； Published online： 2015-05-25 09:53

URL： www.cnki.net/KCMS/detail/11.1929.V.20150525.0953.002.html

Foundation items： National Natural Science Foundation of China (JC-201103); Aeronautical Science Foundation of China (2013ZD53057)

*Corresponding author. Tel.： 029-88491224-15 E-mail: zkzhang@nwpu.edu.cn

Numerical prediction of optimal height of roughness strip for artificial transition on swept wings

TIAN Yongqiang1, ZHANG Zhengke1,*, QU Ke2, ZHAI Qi1

1.NationalKeyLaboratoryofScienceandTechnologyonAerodynamicalDesignandResearch,NorthwesternPolytechnicalUniversity，Xi’an710072,China2.DepartmentofCivilEngineering,CityCollege,TheCityUniversityofNewYork,NewYorkNY10031,USA

A brief introduction toγ-Reθtransition model based on local variables is presented. The model is applied in predicting the transition on swept wings and in determining the optimal height of the roughness strip in artificial transition and the atmospheric flight Reynolds number which can be simulated by the optimal roughness height. In order to validate the ability ofγ-Reθmodel in predicting transition on sweep wings, boundary layer transition on ONERA M6 wing and DLR-F4 standard model wing are predicted, Reynolds-averaged Navier-Stokes (RANS) equations are solved via structured mesh and finite volume method and skin friction coefficient distributions are acquired, thus the transition locations are acquired, which coincide well with the experimental results, conclusions can be made that the predicting results by this model are reliable. Then roughness trips are fixed on DLR-F4 standard model wing surface and transition locations are acquired via the same method, the results reveal that at Mach number of 0.785 and Reynolds number of 3×106, the optimal height of the roughness strip for artificial transition on DLR-F4 standard model wing is 0.11 mm. The simulating ability of artificial transition to atmospheric flight transition is validated by moving the transition location upward via increasing the Reynolds number, results of which indicate that models with the optimal roughness strip height can simulate atmospheric flight free transition at high Reynolds number.

artificial transition; roughness strip height; transition model; swept wings; Reynolds number; boundary layer

2015-03-03；退修日期：2015-03-17；录用日期：2015-05-08； < class="emphasis_bold">网络出版时间：

时间： 2015-05-25 09:53

www.cnki.net/KCMS/detail/11.1929.V.20150525.0953.002.html

国家自然科学基金 (JC-201103)； 航空科学基金 (2013ZD53057)

.Tel.： 029-88491224-15 E-mail: zkzhang@nwpu.edu.cn

田永强， 张正科， 屈科， 等． 后掠机翼人工转捩最佳粗糙带高度数值预测[J]． 航空学报, 2016, 37(2): 461-474. TIAN Y Q, ZHANG Z K, QU K, et al. Numerical prediction of optimal height of roughness strip for artificial transition on swept wings[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(2): 461-474.

http://hkxb.buaa.edu.cn hkxb@buaa.edu.cn

10.7527/S1000-6893.2015.0129

V211.3

： A

： 1000-6893(2016)02-0461-14

*