基于缺陷状态下碗扣式钢管模板支架体系承载力的分析与计算

刘杭杭,吴志新,项炳泉,刘 勇

（安徽省建筑科学研究设计院，合肥，230001）

基于缺陷状态下碗扣式钢管模板支架体系承载力的分析与计算

刘杭杭,吴志新,项炳泉,刘 勇

（安徽省建筑科学研究设计院，合肥，230001）

以碗扣式模板支架试验架体为研究对象，运用JGJ130-2011中碗扣钢管支架的承载力计算方法，计算在材料缺陷、荷载偏心条件下支架的强度、刚度和稳定承载力，结合有限元模拟和试验的结果，对比分析支架的理论计算结果与试验结果的差异，提出重视支架搭设和钢管的质量控制的必要性，指导施工实践。

碗扣式钢管支架系统；稳定承载力；ANSYS模拟

0 引 言

的基础上，采用合理的计算方法和施工方案，来保证碗扣式脚手架的安全与可靠，减少施工风险与事故，实现安全、可靠地施工至关重要[1]。

材料缺陷和荷载偏心在支架体系的施工中经常出现，而且是不可预控的，给支架承载力和稳定性造成不利的影响，因此在支架搭设过程中，钢管的筛选和搭设质量过程控制显得尤为重要。本文以理论计算和试验研究相结合的方法，分析材料缺陷和荷载偏心对支架的承载安全的影响，

碗扣式支撑体系在高架桥梁和地铁等施工中得到了广泛应用，但是，碗扣式模板支架的工程事故时常发生，给国家和人民带来了极大损失。究其原因，主要是由于设计理论不完善、构件配件质量问题、施工质量问题或管理的疏忽等原因造成的，目前部分专家和学者对支架体系相关规范和理论提出质疑。因此怎样在符合脚手架规范指导施工实践。

1 钢管模板支架的承载力计算

1.1 试验模型的荷载计算

1.1.1 试验架体尺寸

本试验钢管支架采用φ48×3.5 mm钢管搭设，材质为Q235。纵横向各4跨，立杆间距900 mm，支架步距1200 mm，架顶高5 m，地杆高300 mm，天杆高500 mm，架体四周设竖向斜支撑，顶层和底层布置水平斜支撑。顶托上主龙骨为φ48×3.5 mm圆钢，间距为 900 mm，次龙骨为100 mm×100 mm 的方木，间距为100 mm[2]。

1.1.2 计算依据

荷载首先作用在分配梁上，按照“分配梁→荷载板→纵横向水平方木→顶托上的圆钢→可调顶托→立杆→底托→基础”的传力顺序，分别进行强度、刚度和稳定性验算。

计算参数：（1）方木 5 KN/m³，荷载板620 kg，分配梁500 kg，千斤顶加至530 KN；（2）碗扣式钢管支架 Ф48 mm×3.5 mm，间距 900 mm×900 mm，水平杆步距 1200 mm；（3）支撑体系放置在钢筋混凝土垫层上。

1.1.3 理想状态下碗扣式钢管支架各部分计算参数

（1）按四跨连续梁计算。方木的自重g1=0.05 KN/m（计算），其他施加恒载g2=8.35 KN/m，g=1.2×（g1+g2），方木弹性模量E=9000 N/mm²；方木惯性矩 I=bh3/12=100×1003/12=8.333×106mm4。方木计算简图见图1[3]。

图1方木计算简图

（2）根据JGJ130－2011，托梁受力按四跨连续梁计算，承受本身自重及上部方木传来的双重荷载，但由于托梁自重相对于承受的外荷载太小，因此忽略，则P=3.63 KN，托梁弹性模量E=2.06x105N/mm²；托梁惯性矩 I=π（D4-d4）/64=1.219×105mm4，抵抗W=5.078x103mm³。其托梁计算简图见图2。

图2托梁计算简图

（3）立杆的截面特性，外径D=4 8 m m，壁厚t=3.5 mm，截面积A=489.3 mm²，惯性矩I=1.219×105mm4，抵抗距W=5.078×103mm³，回转半径i=15.784 mm，抗弯设计强度fm=205 N/mm²。经计算梅根立杆承受荷载N=lx×ly×g =33.42 KN。

1.1.4 在考虑缺陷及市场支架实际尺寸状态下碗扣式钢管支架各部分计算参数

（1）采用100×100 mm方木，考虑方木实际负偏差和压刨量，计算时尺寸按照90×90 mm考虑；抗弯强度设计值fm=15 N/mm²。方木的自重g1=0.05 KN/m（计算），其他施加恒载g2=8.35 KN/m，方木弹性模量E=9000 N/mm²；方木惯性矩I=bh3/12=90×903/12=5.468×106mm4，截面抵抗矩Wn=bh2/6=1.215×105mm³。

（2）方木的摆设位置（即集中荷载的作用位置）直接决定了荷载的传递，上面方木是按从节点开始均匀的放置且每个节点都有方木作用，其实这种理想状态在实际情况很难出现，下面调整方木不再通过每支立杆的顶点。托梁计算简图见图3。

图3托梁计算简图

3）由《直缝电焊钢管》和《低压流体输送用焊接钢管》规范知，支架钢管的外径偏差应在±5 mm范围内，壁厚应在±10%t（t为钢管的壁厚）范围内。

本文按以下两种情况将立杆作为压弯构件来考虑立杆壁厚及外径最大偏差的影响。1）支架采用Φ48×3.25，立杆间距900×900 mm，步距1200 mm。抗弯强度设计值fm=205 N/mm²，截面积A=457 mm²，惯性矩I=1.136×105mm4，抵抗距W=4.732x103mm³；2）支架采用Φ43×3.5，立杆间距900×900 mm，步距1200 mm。抗弯强度设计值：fm=205 N/mm²，惯性矩I=8.537×104mm4，抵抗矩W=3.97×103mm³,截面积434.326 mm²。

1.2 试验模型的的受力验算

受弯构件强度与刚度验算，如式（1）[4]。

其中σ为弯曲正应力，M为构件的最大弯矩，W为净截面模量，f为抗弯强度设计值。

轴心受力构件稳定性验算,如式（2）[4]。

N为构件的轴压力，ϕ是轴心受压立杆的稳定系数，根据长细比λ按《规程》附录C采用；A是立杆的截面面积，f是钢材抗压强度设计值，取f=205 N/mm²。

压弯构件强度与稳定性验算,如式（3），（4）[5]。

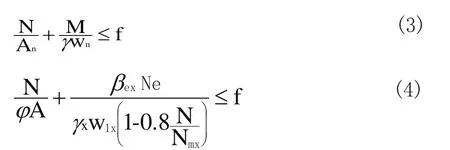
N为构件受到的轴心压力；

ϕ为弯矩作用平面内的轴心受压构件稳定系数；

A为构件截面面积；βmx为等效弯矩系数βmx=0.65+0.35M2/M1 ；

e为附加偏心距这里取5 cm； xγ为与截面模量相应的截面塑性发展系数；

w1x为在弯矩作用平面内对较大受压纤维的毛截面模量；

f为钢材抗 压 强 度 设 计 值; Nex为 参数，Nex=π2EA/（1.1xλ2）。

考虑几种缺陷状态对支撑体系的承载力影响分析

本文主要考虑3种缺陷或偏差对支撑体系的承载力影响，如下：①方木实际负偏差和压刨量；②方木的摆设位置的偏差；③立杆偏心受压及立杆壁厚和外径偏差。在考虑缺陷状态对支撑体系承载力的影响见表1~表2。

表1在考虑①和②缺陷对方木和托梁承载力影响的对比表

方木受弯承载设计值f=15 N/mm²，托梁受弯承载设计值f=205 N/mm²，从表1得出，方木和托梁抗弯验算均满足要求。但方木实际负偏差和压刨量，使方木受弯承载力的储备降低了将近10%，托梁在缺陷条件下受弯承载力降低近20%，因此安装和材料的缺陷对支架承载力的影响是不可以忽略的。

表2在考虑③缺陷下对立杆承载力影响的对比表

在理想条件下对于轴压细长杆件，在杆件没有栓孔等缺陷时，往往只需要考虑它的稳定性。由表2可得，在考虑壁厚、荷载偏心及外径偏差的影响时，失稳验算均能满足承载力要求，但在荷载偏心时，强度验算不满足承载力要求。荷载偏心对支架的强度验算比失稳验算更为重要。

2 有限元模拟和试验结果

2.1 有限元模拟计算

2.1.1 模型的建立

运用ANSYS有限元软件对试验支撑架的极限承载力进行模拟计算，模型按1:1尺寸建模（见图4），支架平面尺寸3.6 m×3.6 m，支架高5.0 m。参数选取：钢管直径48 mm，壁厚3.5 mm，弹性模量Es=2.06×106 MPa，泊松比ν=0.3；约束与加载：支架与支撑面之间采用铰接，碗扣节点在纵向和横向截面内采用铰接方式连接（见图5）；模拟分析过程分为线性屈曲分析和非线性屈曲分析两个步骤，线性屈曲分析时竖向荷载F=2.5 kN，采用扩展计算得出三阶模态，非线性屈曲分析时，竖向荷载按线性分析的临界载作为试算荷载并施加很小的水平向扰动荷载[2]。

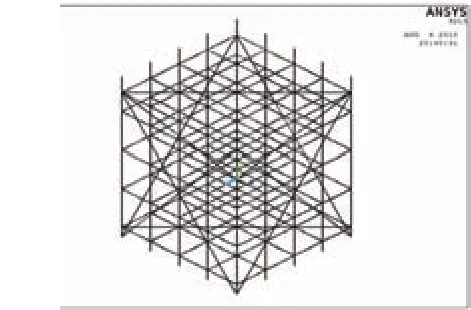
图4 三维模型

图5 约束与加载方式

2.1.2 模拟结果分析

线性性屈曲分析（失稳分析）基于线性理想结构的假设进行分析，所以该方法的结果偏大，在设计中不宜直接采用分析结果，但线性屈曲分析结果可以作为非线性屈曲分析的试算荷载。模态分析结果取前三阶模态（见图6-图8），屈曲模态图见图4。非线性屈分析属于大变形的静力学分析，在分析中将压力扩展到结构承受极限载荷。使用非线性屈曲分析方法得到的临界载荷一般较线性方法小，因此在非线性分析中通常使用线性分析中的临界载荷为试算荷载的起点，分析结果出现屈曲后的变化形态[2]（见图9）。

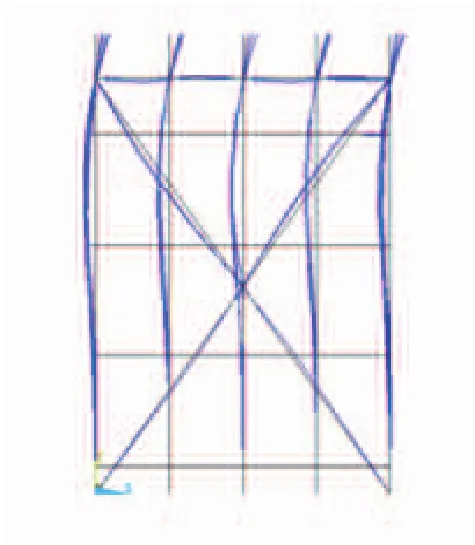
图6 一阶屈曲模态

图7 二阶屈曲模态

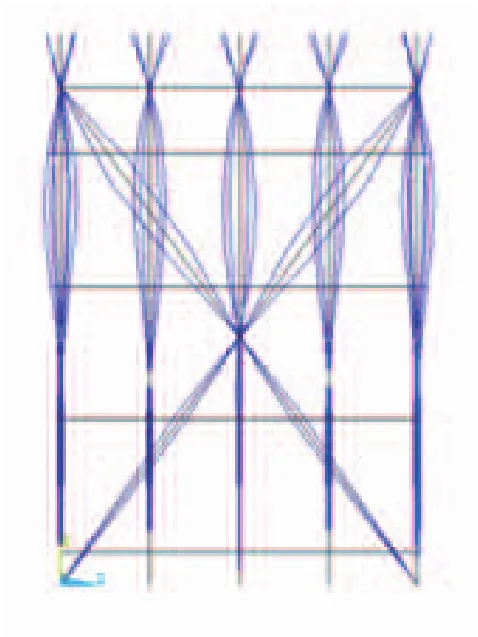
图8 三阶屈曲模态

图9 荷载与位移曲线图

工程中取一阶模态频率数值与荷载值的乘积作为线性屈曲结果。一阶模态频率数值fact=0.34664×106，荷载F=2.5 N，线性屈曲荷载Fcr=fact×F=2.5×0.34664×106=866.6 kN。

由模拟结果(图9)整理可得：

（1）支架受力状态可以分为三个阶段：

a)荷载小于500 kN，基本为线弹性阶段；

b)荷载在500 kN~625 kN之间，为弹塑性阶段；

c)荷载大于625 kN，进入屈服阶段。

（2）曲线发生突变点，即为结构屈曲的发生点，失稳承载力取为625 kN。

2.2 承载力试验结果

本次试验所用的钢管和木楞均从施工现场随机选取，由现场施工人员在安徽建筑大学土木学院实验室搭设安装，其目的是为了更接近地铁站的模板支架的材料和搭设状况。

试验破坏过程：试验荷载加至500 kN时，支架进入失稳阶段，失稳始于南边第二榀，立杆面外位移明显较大，且均向同一方向屈曲，呈中间部位外突，两头内缩状。当荷载加至530 kN时，支架结构进入破坏状态，中间立杆出现面外较大位移，持荷过程中掉载超过了本级荷载的1/8，试验停止。本次试验模板支架承载力取为530 kN。

3 结语

（1）由计算结果得出，构件的材料缺陷和荷载偏心对模板支架承载力影响是不可忽略的。在支架承载力设计时，取材料的偏差下限计算，并适当考虑荷载偏心对支架承载的影响。

（2）模板支架的承载力模拟结果（625 kN）超出试验结果（530 kN）的约18%，主要原因在于计算模型未考虑材料缺陷和加载偏心。在模板支架的施工实践中，采用更精细的承载力分析方法，优化设计，节省材料；或在设计时留有更多的承载力安全储备。

（3）建议施工前，对钢管截面尺寸、平直度应随机抽检，偏差超出规范要求的严格禁用。模板支架搭设过程要严格监控，保证每个节点牢固，横竖杆可靠连接，减小材料缺陷和荷载偏心对模板支架承载力稳定的影响。

(下转第3 4页)

Analysis and Computation of Bearing Capacity of Bowl-Scaffold System under Defective Condition

LIU Hanghang, WU Zhixin, XIANG Bingquan, LIU Yong

(Anhui Institute of Building Research &Design, Hefei, 230001,china)

This paper aims to conduct research on the bowl- full hall scaffold. The strength, stiffness and stable bearing capacity of scaffold under the conditions of the defective material and eccentric load are calculated by using the method of bowl-scaffold bearing capacity in JGJ130-2011. According to the comparison and analysis of the differences between theoretical calculation and experimental results as well as the combination of finite element simulation and experimental results, it is put forward that more attention should be paid to the scaffold linking and the quality of steel pipe is proposed, which can be used to guide in construction practice.

bowl-scaffold system；stable bearing force；ANSYS simulation

TU731.2

A

2095-8382(2016)06-026-04

10.11921/j.issn.2095-8382.20160606

2016-01-11

刘杭杭（1987-），硕士研究生，主要研究方向：结构力学及其应用。