谈数学直觉思维的培养策略

张磊

（韩山师范学院数学与统计学院，广东潮州 521041）

谈数学直觉思维的培养策略

张磊

（韩山师范学院数学与统计学院，广东潮州 521041）

数学直觉思维是以一定的知识经验为基础，通过对数学对象的结构及其关系作整体观察，在一瞬间领悟到对象的某方面的本质，从而迅速做出判断的一种认知能力.学生一旦有了某个知识的数学直觉，就可加深对该知识的理解，既提升了学生的形象思维，又对抽象思维予以支撑，有利于认清数学本质.在具体的数学教学中，要通过创设数学实验、增强直觉感知，展示实物模型、提升直觉能力，寻找数学原型、加深直觉认识，借助联想思维、拓展直觉深度等策略，来培养中学生的数学直觉思维能力.

中学生；数学直觉；培养；策略

笔者常常听到一些中学数学教师抱怨：学生缺乏数学直觉，培养学生的数学直觉能力非常困难.经常会遇到许多学生对做题的结果缺乏基本的直觉认识，比如在求sina值时，有学生计算出值为2，就作为答案照写不误；再如求椭圆离心率时，有学生算出结果为 2，也不假思索地作为答案.如果单纯地问这些学生：sina与椭圆离心率的范围是多少？他们会毫不犹豫地回答：[-1,1]和（0,1）.那为何学生明明知道这些知识点，而在做题时却写出不在这个结论范围之内的答案呢？笔者认为原因是多方面的，但有一点不可否认，那就是学生只简单地记住了表面上的结论，而没有去深刻理解这个结论，也没有纳入到自己已有的认知结构中去，于是导致做题得出的结果与记住的结论孤立开来，没有整合为一个整体，变成了“两张皮”.说到底，现在的中学生缺少数学直觉.

1 对数学直觉的认识

一般认为，数学直觉思维是以一定的知识经验为基础，通过对数学对象（结构及其关系）作整体观察，在一瞬间领悟到对象的某方面的本质，从而迅速做出判断的一种认知能力.它凭借已有的经验知识信息，不受某种逻辑规则的约束，但受逻辑规则的指导，通过想象、猜测以及高速高效的对比、分析、转换、综合等，对事物作出直接的估断或预见[1-3].直觉思维可分为想象型和灵感型，想象型是一般的直觉思维形式，灵感型表现为人们对长期探索而未解决问题的一种突然性领悟，也就是对问题百思不得其解时的一种“茅塞顿开”[4].因而数学直觉思维具有非逻辑性、创造性、突发性、偶然性、或然性、经验性等[5-6].但从培养数学直觉思维能力的角度来看，笔者认为它具有以下几个特点：

1.1 非逻辑性

直觉思维的非逻辑性，是它的本质特性.直觉思维并不是根据一定的规律按部就班地进行的，它不是归纳式的概括也不是演绎式的推理，同分析和综合逻辑方法也不一样，它是依靠思维中的想象、猜测和测察力等非逻辑功能去直接地把握对象的[7].它并不遵循固定的逻辑规则，相反的，它有意或无意地打破固定的不变的逻辑规则的束缚，在非逻辑方面另辟蹊径.当然这并不意味直觉思维排斥逻辑思维，事实上，逻辑思维对直觉思维具有诱导作用，在直觉思维中有时要借助于逻辑思维的方法.

1.2 创造性

现代社会需要创造性的人才，我国的教材由于长期以来借鉴国外的经验，过多的注重培养逻辑思维，培养的人才大多数习惯于按部就班、墨守成规，缺乏创造能力和开拓精神.直觉思维是基于研究对象整体上的把握，不专意于细节的推敲，是思维的大手笔.正是由于思维的无意识性，它的想象才是丰富的，发散的，使人的认知结构向外无限扩展，因而具有反常规律的独创性[8].因此，直觉思维能产生新的认识和发现，真正可贵的因素是直觉，爱因斯坦说，科学原理虽然是以直接经验为基础，但是原理的发现，并没有逻辑的道路，只有通过那种以对经验的共鸣的理解为依据的直觉.

1.3 简约性

直觉思维是对思维对象从整体上考察，调动自己的全部知识经验，通过丰富的想象作出的敏锐而迅速的假设、猜想或判断，它省去了一步一步分析推理的中间环节，而采取了“跳跃式”的形式[9].它是一瞬间的思维火花，是长期积累上的一种升华，是思维者的灵感和顿悟，是思维过程的高度简化，但是它却清晰的触及到事物的“本质”.

1.4 自信力

学生对数学产生兴趣的原因有两种，一种是教师的人格魅力，其二是来自数学本身的魅力[10].不可否认情感的重要作用，但笔者的观点是，兴趣更多来自数学本身.成功可以培养一个人的自信，直觉发现伴随着很强的“自信心”.相比其它的物质奖励和情感激励，这种自信更稳定、更持久.当一个问题不用通过逻辑证明的形式而是通过自己的直觉获得，那么成功带给他的震撼是巨大的，内心将会产生一种强大的学习钻研动力，从而更加相信自己的能力[11].高斯在小学时就能解决问题“1+2+ 3+…+99+100=？”，这是基于他对数的敏感性的超常把握，这对他一生的成功产生了不可磨灭的影响.而现在的中学生极少具有直觉思维，对有限的直觉也半信半疑，不能从整体上驾驭问题，也就无法形成自信.

2 数学直觉的培养意义

“数学王子”高斯曾经反复强调，他的数学发现主要来自经验，“证明只是补行的手续”.德国数学家伊恩·斯图加特也说：“直觉是真正的数学家赖以生存的东西”.美籍匈牙利数学家波利亚也曾说过：“直观的洞察和逻辑的证明是感知真理的两种不同方式——直观的洞察可能远远超前于形式逻辑的证明.”[12]纵观人类科技进步发展史，许多重大的发现都是基于直觉：欧几里得几何学的五个公式就是基于直觉，从而建立起欧几里得几何学这栋辉煌的大厦；哈密顿是在散步的路上迸发出了构造四元素的火花；阿基米德在浴室里找到了辨别王冠真假的方法；凯库勒发现苯分子环状结构更是一个直觉思维的成功典范.

认知心理学家认为学生学习数学新知的过程，就是一个自我建构的过程，人的大脑会根据已有的认知基础，对新知进行加工和重新组合，以形成一个新的结构体系，而要熟知这个新结构，就必须要对刚纳入的新知有一个直觉的认识，这就需要学生通过自己的亲身体验和领悟才会有直观的感觉，留下的印象也更加深刻，可能还会体验到成功的喜悦，从而更能激发起对数学学习的兴趣.

所以，学生一旦在脑中有了某个知识的数学直觉，不仅可加深学生对此知识的理解，特别是某些抽象性强、难于理解的概念、法则与结论等，还可增强学生的形象思维，并对抽象思维予以支撑.当然，最直接的好处便是解题时学生有了直觉思维，可以更简单便捷地认识到题目的本质，这就是培养数学直觉的意义所在.当然这种数学直觉能力需要教师的有意识培养，比如可通过一些具体图形、模型或生活中的数学现实等，以提升直觉能力.

3 数学直觉的培养策略

新课程标准指出：“学生的数学学习活动不应只限于接受、记忆、模仿和练习，高中数学课程还应倡导自主探究、动手实践、合作交流、阅读自学等学习数学的方式.”[13]因此从新课程实施的这几年来，工作在第一线的数学教师也基本上接受了这些新的教学理念.比如对于概念、定理、公式等的新授课都能安排局部探究和小组合作，尽量在课堂上调动学生的积极性和发挥学生的主观能动性，并能将学生合作与独立思考综合起来运用.当然，除此之外，还可以动手实践、直观感知、操作确认等学习方法，这给数学直觉的培养方式指明了方向.笔者结合这几年在中学的听课经历，谈谈培养数学直觉的一些策略.

3.1 策略一：创设数学实验，增强直觉感知

当学生难以发现所学知识结论和相互间的关系或规律时，可通过创设数学实验，让学生进行动手操作实践，以体验数学发现的过程，增强对所学知识的直觉感知.

那何谓数学实验呢？笔者认为数学实验就是实验者借助于一些道具或仪器，通过自己动手进行亲自感受与体验，并在一定思维活动下得出的规律和结论或者验证了某项猜想和理论的探究活动.当然，这些数学实验除了动手操作外还一定要有思维活动的参与.

现在许多有条件的中学都在使用图形计算器，并把它作为一项数学实验来操作.笔者不反对这种形式的数学实验，但以现在我国的教学现状来看，绝大多数学校还不具有这样的装备，如果让学生自备更不现实.所以本文提到的数学实验更有点类似于物理或化学形式的实验，道具或仪器可以自己简易制作.

正因为数学实验是通过学生自己的操作实践，所以可形成最初的直观感知，继而通过思考想象，再到发现、归纳、猜想，使学生亲历数学知识的建构过程，便于发现数学规律，增强数学直觉.

案例1让椭圆“圆”形毕露

在《椭圆》的第1课时教学中，大多数高中数学教师采用的基本流程是：教师先用绳子画椭圆，再归纳出椭圆定义，然后建立椭圆方程，教师讲解例题与练习.笔者发现在这个按照教材编写的顺序进行教学时，学生总有一种莫名其妙的感觉：那就是所学的椭圆与圆毫无关系.可既然无关系，为什么“椭圆”中有个“圆”字呢？因此学生心目中的“椭圆”应该会与圆有一定的联系，至少它们外表“相近”，即是“椭”的圆.由于“椭圆”给人的感觉是一个长圆形，是由圆“压扁”或“伸长”而成的，那教师为什么不提圆呢？所以，学生心中觉得这个椭圆纯粹是“空降”而来，既没有人情味也感到不合常理，从而产生一种不自然感，也降低了学生对椭圆的直觉认识.为此，笔者认为在引入上不妨进行实验改进.

引入时的实验可这样设计：先让同桌俩同学合作，用一条细绳子在纸上按住两端点画出椭圆，然后让同学探究：当两端点离得越来越近和越来越远时椭圆的形状变化.

通过学生的实验操作，就会发现：当两端点越来越近时，画出的椭圆越来越圆，当两端点重合时就变成了圆；而当两端点离得越来越远时，画出的椭圆就越扁.这样学生就会自己研究出椭圆与圆的关系，从而对椭圆的得出不会感到突然，也增强了对椭圆的直观认识，同时还为椭圆离心率的大小影响椭圆形状的知识埋下了伏笔：当椭圆越圆，e就越小，当e=0时就变了圆；椭圆越扁，e越大，当e→a时，e→1.有了这样的动手实验，学生对圆与椭圆的形状及e的范围在（0,1）有了直观感受，而脑中有了这样的直觉感知，也就不会出现当e=2时还作为椭圆离心率答案的错误现象，因为学生通过自己的实验操作而产生的印象远比老师空洞说教要深刻得多.

3.2 策略二：展示实物模型，提升直觉能力

在讲授一个新的数学知识，尤其是抽象性比较强、学生一时难以理解或不能想象的数学知识时，就要联系学生生活中可见到的实物，以帮助学生理解，增加直观性.笔者认为教师通过实物模型的展示是培养学生数学直觉的一个不错选择.因为具体的实物模型可以降低抽象难度，提升直观形象.特别是在讲授立体几何知识时，更需要用实物模型来直观认知，再通过实验操作来确认，这样才能消除学生初中所学的平面几何带来的认知障碍，增强学生的空间想象能力.所以中学教师在面对学生较难理解的三维空间的立体图形时，最佳的教学策略便是教师要多提供一些具体的实物模型，并让学生自己也动手做一做，尤其是遇到翻折类的题型时，一定要让学生多动手操作以增强直观形象，提升直觉能力.

案例2棱柱欧氏定义的反例

笔者在听中学教师讲授棱柱定义这节课时，一般都会让学生判断这样一个命题：“有两个面平行，其余各面都是平行四边形的多面体是棱柱”.而学生往往会认为是对的，此时教师就会给出一个如图1的反例，以此来说明该命题的错误，从而佐证教材上的棱柱定义是正确的.显然这个反例学生是较难想到的，因而需要教师告之.但事实上这个反例是有缺陷的，因为一般情况下的多面体都是指凸多面体，而该反例却是凹的，因此数学程度好的学生会质疑，从而就很难判断上述命题的真假.

其实，有数学史知识的教师应该知道，这个命题就是2 000多年前的古希腊数学家欧几里得（Euclid，前330～前275）在《几何原本》中下的棱柱定义，简称欧氏定义.当然现在知道这个定义是不对的，但就是这个错误的定义却得到了历史上许多数学家的认可，并整整统治了2 000多年，其原因就是长时间找不到欧氏定义的反例.也许中学教师会认为图1的反例并不是很难，数学家怎么会想不到呢？所以问题就在于这个反例是凹的，可能当时欧几里得就已经知道这个例子了，但他并不认可，因此只有找到一个凸的反例才具有说服力.在人类历史上正是在找这个凸的反例时，让数学家们整整花了2 000多年，直到20世纪初才找到，该反例便是图2[14].很明显，这个凸的反例学生根本想不到，这就需要教师自己动手做这个反例的实物模型，用事实说话来提升学生的直觉能力.

用实物模型来展现，可以让学生感到既直观明了又生动具体，从而使一些结论深刻地印在学生的脑海里.如案例2，学生看到这个凸的反例实物时一定会留下深刻印象的.事实上，数学中除了立体几何外，还有一些比较抽象的概念也可借助实物模型来理解，如向量的概念，可用学生手中的“笔”来替代：笔尖表示向量方向，笔身表示向量的模，笔的移动表示向量的平移，这样学生就会很快理解与“数”不同的“向量”；再如任意角的概念，可用学生身上的“手表”或教室里的“钟”等实物来展现，就会让学生很快突破以前所学的角范围所带来的束缚.

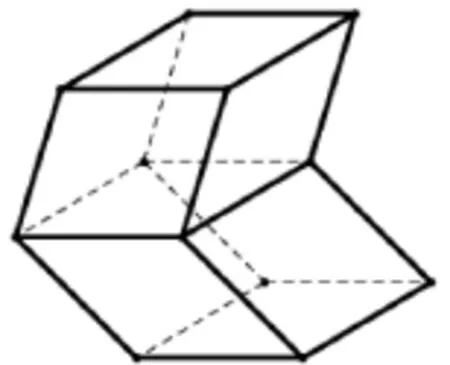
图1

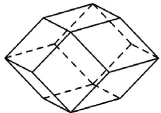
图2

3.3 策略三：寻找数学原型，加深直觉认识

“随着数学学习的深入，学生积累的数学知识和方法就成为了学生的‘数学现实’.这些现实应当成为学生进一步学习的素材，选用这些素材，不仅有利于学生理解所学知识的内涵，还能够更好地揭示相关数学知识之间的内在关联，有利于学生从整体上理解数学，构建数学认知结构”[15].根据对“数学现实”的诠释，笔者认为可从学生已有生活常识出发，寻找数学知识原型，以加深直觉认识.

数学原型，其实就是指产生数学概念、法则、定理等知识的生活来源，或已得到论证的数学知识来作为直觉认识的一种模型.它包括日常生活中的原型和所学的数学知识作为模型.实际上，学生在前面的数学学习中也一直在利用数学原型，比如通过“向东向西”、“零上零下温度”（数学原型）来形成“相反意义的量”，继而来进一步理解“正负数”和“正负数加减法则”[15]；因式分解可由小学里学过的数的质因数分解作为数学原型来理解等等.

案例3“糖水不等式”的教学

在必修5《不等关系与不等式》的教学中，新课程标准教学要求“通过具体情境，感受在现实世界和日常生活中存在着大量的不等关系，了解不等式的现实背景.”比旧的教学大纲更侧重于通过具体的情境让学生感受新知，增加了对分析处理具体问题的要求.为了使学生在教师的引导下能通过直觉发现“糖水不等式”，并对该不等式的正确性有充分的认识，教师可以设计出如下的问题链：

问题1：同学们都知道，给糖水加糖能使糖水变甜.你们能把这一生活常识用数学式表达出来呢？（大部分学生可能会面露难色，不知从什么地方下手，原因是这里既没有数字又没有字母.面对此情景，教师继续引导.）

问题2：解应用题列方程式时，未知数肯定没有具体数据，那时你们是怎么办的？（问题2使学生联想到用字母表示数：设原来的糖水浓度为t1，加糖后的浓度为t2，则有

针对学生的思考，教师首先肯定他们抓住了问题的本质，即建立起一个不等式.教师紧接着抛出问题3.）

问题3：不足的是，式（1）没有直接反映出“浓度”与“加糖”.你们能不能更具体地表示出“原浓度”、“加糖后的浓度”以及两个浓度间的关系，使人一看这个“没有任何汉字”的“符号”不等式，就能领会“糖水加糖更甜了”？（问题3会促使学生想到：设b克糖水里有a克糖，则，加糖后的糖水更甜了，就存在c＞0，使

当看到学生给出（2）式时，教师提出问题4.）

问题4：这里的c表示什么？是表示糖的质量吗？浓度与质量能够相加吗！（问题4促使学生对（2）式中量的统一性产生思考，当学生们若有所思时，教师进一步追问.）

问题5：（2）式只表示了浓度增加则糖水就更甜，还没有把浓度增加的原因——添糖反映出来.换句话说，当时，t2如何表示？（在问题5的刺激下，学生们会恍然大悟：，其中m＞0为所添糖的质量.由此得不等式：对b＞a＞0，m＞0，有.）

在原本比较枯燥的不等式教学中，教师从学生的已有生活常识出发，借助生活中的“给糖水加糖能使糖水变甜”这一数学原型引入，这样不仅让学生感受到生活中不等关系的存在，也知道生活中数学无处不在，激发起学生学习兴趣的同时，加深了学生对“糖水不等式”的直觉认识，通过教师系列问题的“启”和“发”使学生达到“愤”和“徘”的状态，把学生的直觉思维一步一步地引向深入，引导学生达成对新知的高效认知.

又如，高中数学中的一些概念、性质和公式等也可通过寻找数学原型来帮助理解.比如：三角函数的单位圆定义，就以游乐场中的摩天轮作为数学原型：你坐在那里的位置就相当于单位圆上的一个点，然后当摩天轮转动后，如何来表示你的位置？以这样的生活现实来帮助学生认识三角函数的本质：刻画具有周期性现象的圆周运动的函数模型.学生有了摩天轮作为单位圆的一个数学原型后，自然就会直观认识到，的值不能超过1，同时有了这样的数学直觉，也就不会犯算出sinα=2还作为答案的错误情况.再比如一些抽象函数，当具有性质时，则前者可用指数函数作为模型，后者可用对数函数f(x)f(y)=f(x+y)，f(xy)=f(x)+f(y)作为模型.这样让学生用已熟悉的具体函数作为数学原型就好理解，也容易解题了.

3.4 策略四：借助联想思维，拓展直觉深度

联想思维是产生直觉的先导.联想是学生在认识数学对象的过程中，根据数学对象之间的某种联系，由一个数学对象想到另一个相关数学对象的心理活动过程.数学问题解决的思维过程实质上是已知和未知间的一系列的联想过程.当学生面对某些待解决且难以突破的新颖问题时，教师可引导学生通过仔细的观察，必要时画出示意图，并联想到一些思考方法接近的、形式相同的、结构特征相似的熟悉问题或常规问题，通过迁移将会顿悟出解决问题的思路和方法.

案例4祖暅原理的教学

为了使学生在教师的启发下能通过直觉发现祖暅原理，并对该原理的正确性有充分的认识，教师可以先提出平面上的如下问题：

①不规则的图形我们可以采用哪些方法求出它的面积的近似值？

②夹在两条平行线间的两个平面图形被平行于这两条直线的任意直线所截，如果截得的长度总相等，那么它们的面积有什么关系？你能说明理由吗？

通过联想，学生发现用平行分割、以直代曲的方法可把两平面图形的面积分成等积的平行四边形或梯形的面积之和.易见二者面积的近似值是相等的.当分割数无限增大时，便可得出二者的面积相等的结论.教师紧接着又提出第三个问题：

③由以上的结论，请你猜想在空间会有什么类似的结论？你能说明其中大概的理由吗？

以上过程中，教师由于引导学生进行渐进式的类比联想，使学生不断产生新的直觉最终“发现”祖暅原理，从而产生了认识上的飞跃.尽管其中的推理不甚严格，但却使学生感受到了无限细分求和的极限思想.事实上，数学上的任何重大突破都萌发于这类朴素的直觉或灵感.

当然，数学中的联想是多层次多角度的，除类比联想、形似联想外，还有对比联想、接近联想、关系联想等等.但无论何种联想都要以合理的数学认知结构为基础，以合情的思维导向为原则.正确的联想所引发的直觉往往可以在解题中收到“柳暗花明，曲径通幽”的效果.

图3

4 培养数学直觉需注意的问题与原则

我们在采用上述策略培养学生数学直觉能力的时候，需注意防止以下问题：其一，目的性不明.培养数学直觉是为了增强学生对所学知识的直观认识，也是让学生更好地理解数学知识，认清数学本质.如果仅仅是为了体现直观性，而忽视数学知识的内在联系和逻辑性，尤其是脱离数学的本质，那这样就只停留在直觉的表象，对学生无任何帮助.其二，缺乏科学性，盲目培养.不管是数学实验还是数学现实中的原型，都是对数学知识的直观诠释，即都能正确地刻画数学知识.如果教师提供的模型并不能让学生很好地理解数学知识，甚至是错误的，不仅不能培养数学直觉，而且还会误导学生.

为了避免在培养数学直觉时出现上述两个问题，需遵循一些原则：其一，适用性原则.不管设计的是数学实验，还是提供实物模型和数学原型等，都要根据教学内容和学生已有的数学认知程度来考虑，只有正确反映数学知识的直观教学才适用于学生，也有利于学生理解数学.其二，直观性原则.教师让学生完成某个数学实验，再现某数学知识或展示某个模型，都要让学生感到直观形象，从而使学生能完成从感性认识到理性认识的顺利过渡，提高学生的抽象思维能力，同时也加深直觉印象.其三，探究性原则.学生做完数学实验后或在教师提供模型后，还要让学生继续探究，或观察发现或归纳总结等，如案例1.而案例2，当学生看到实物模型后，还可深入探究怎样得到这个反例，如可通过“补形”或“切割”等方法，这就需要推理和数学思维.如果抽象的推理以具体实验或模型为依托，学生在研究实验与模型的过程中就可获得解决问题的启发与灵感.

5 结束语

要让学生在内心真正理解数学知识和接纳新知，就必须要先对该知识有一个直觉感知，然后再在大脑中形成一个整体认识，继而上升到抽象层面.笔者在对中学教师的听课中归纳出来的这四种策略，对学生的数学直觉培养有一定的帮助.发现一个问题往往比解决问题更重要，而“发现”靠的并不都是逻辑思维，直观性的思维和直觉能力有时更能出奇制胜.而在课堂上培养学生的数学直觉，既可使许多抽象和沉闷的概念、公式、定理、结论来得更易理解，也可避免本文开头提到的中学教师所抱怨的这种现象.最后借用荷兰哲学家斯宾诺莎的一句话作为本文的结束语：“只有通过直觉才可能直接认识一件事物的正确本质而不致陷于错误.”

[1]郑君文，张恩华.数学学习论[M].南宁：广西教育出版社，2003.

[2]周治金，赵晓川.直觉研究述评[J].心理科学进展，2005，13（6）：745-751.

[3]陆书环，傅海伦.数学教学论[M].北京：科学出版社，2004.

[4]俞国良.创造力心理学[M].杭州：浙江人民出版社，1996.

[5]汪安圣，朱祖祥.思维心理学习[M].上海：华东师范大学出版社，1992.

[6]喻平.数学教育心理学[M].南宁：广西教育出版社，2004.

[7]格劳斯.数学教与学研究手册[M].上海：上海教育出版社，1999.

[8]邵志芳.思维心理学（第二版）[M].上海：华东师范大学出版社，2007.

[9]朱德全.试论教学场情境的生成策略[J].高等教育研究，2004，25（6）：71-75.

[10]朱水根，王延文.中学数学教学导论[M].北京：教育科学出版社，2001.

[11]张大均.教育心理学（第二版）[M].北京：人民教育出版社，2004.

[12]叶彩虹.浅谈中学数学直观思维能力的培养[J].数学学习与研究，2010（20）：114-115.

[13]中华人民共和国教育部.普通高中数学课程标准[M].北京：人民教育出版社，2006.

[14]沈金兴.一个需要完善的经典反例[J].中学数学，2015（3）：24-25.

[15]张奠宙，林永伟.关于“现实数学”和“数学现实”[J].数学教育学报，2008（2）：1-4.

Strategies for the Cultivation of Mathematic Intuitive Thinking

ZHANG Lei
（College of Mathematics&Statistics,Hanshan Normal University,Chaozhou,Guangdong,521041）

Mathematic intuition thinking is a cognitive ability,which can help one make a judgement quickly on the basis of certain knowledge and experience,by a overall observation of the object(and its constitution and relationships)of mathematics.Once a student gets mathematic intuition for certain knowledge,he/she can have deeper understanding of it,which will promote his/her imagery thinking as well as abstract thinking,so as to recognize the nature of mathematics.In specific mathematics teaching,we can follow four strategies to cultivate middle school students’ability of intuitive thinking:enhance students’perceptual intuition by create mathematic experiment;promote their intuitive abilities by physical model demonstrating;deepen their intuition cognition by finding mathematic prototype;expand depth of their intuition by the help of associative thinking, etc.

middle school students;mathematic intuition;cultivation;strategies

G 427

：A

：1007-6883（2016）06-0083-07

责任编辑 朱本华

2016-10-09

韩山师范学院2015年度教学改革项目（项目编号：HJG1524）.

张磊（1981-），男，河南确山人，韩山师范学院数学与统计学院讲师.